C++ 傅里叶功率谱的计算以及应用

一维傅里叶功率谱的计算

#include <stdio.h>
#include <math.h>

#define pi 3.1415926
#define rows 3
#define colums 5

typedef struct {
    float re;// really 
    float im;// imaginary 
}complex, * pcomplex;

complex complexadd(complex a, complex b) //复数加
{
    complex rt;
    rt.re = a.re + b.re;
    rt.im = a.im + b.im;
    return rt;
}

complex complexMult(complex a, complex b) //复数乘
{
    complex rt;
    rt.re = a.re * b.re - a.im * b.im;
    rt.im = a.im * b.re + a.re * b.im;
    return rt;
}

/// <summary>
/// 离散傅里叶变换
/// </summary>
/// <param name="f">时域数据</param>
/// <param name="F">频域数据</param>
/// <param name="N">数据长度</param>
void dft(complex f[], complex F[], int N) {
    complex temp;
    for (int k = 0; k < N; k++) {
        F[k].re = 0;
        F[k].im = 0;
        for (int n = 0; n < N; n++) {
            double rad = (double)k * n / N;
            temp.re = (float)cos(2 * pi * rad);
            temp.im = -(float)sin(2 * pi * rad);
            F[k] = complexadd(F[k], complexMult(f[n], temp));
        }
    }
}

/// <summary>
/// 离散傅里叶逆变换
/// </summary>
/// <param name="F">频域数据</param>
/// <param name="f">时域数据</param>
/// <param name="N">数据长度</param>
void idft(complex F[], complex f[], int N) {
    complex temp;
    for (int k = 0; k < N; k++) {
        f[k].re = 0;
        f[k].im = 0;
        for (int n = 0; n < N; n++) {
            double rad = (double)k * n / N;
            temp.re = (float)cos(2 * pi * rad);
            temp.im = (float)sin(2 * pi * rad);
            f[k] = complexadd(f[k], complexMult(F[n], temp));
        }
        f[k].re /= N;
        f[k].im /= N;
    }
}

/// <summary>
/// 将零频分量移到频谱中心
/// </summary>
/// <param name="F">频域数据</param>
/// <param name="Shift">零频分量移到频谱中心的数据</param>
/// <param name="N">数据长度</param>
void fftshift(complex F[], complex Shift[], int N) {
    for (int i = 0; i < N; i++) {
        int shiftIndex = (i + (N - 1) / 2 + 1) % N;
        Shift[i] = F[shiftIndex];
    }
}

/// <summary>
/// 计算功率谱函数
/// </summary>
/// <param name="F">零频分量移到频谱中心的数据</param>
/// <param name="P">功率谱数据</param>
/// <param name="N">数据长度</param>
void powerSpectrum(complex F[], float P[], int N) {
    for (int i = 0; i < N; i++) {
        P[i] = F[i].re * F[i].re + F[i].im * F[i].im;
    }
}

int main() {
    complex samples[colums], X[colums]; //samples[]示例

    for (int i = 0; i < colums; i++) {
        samples[i].re = (float)(i + 1);
        samples[i].im = 0;
    }
    dft(samples, X, colums);
    printf("一维傅里叶变换 DFI:\n");
    for (int i = 0; i < colums; i++) {
        printf("(%f,%f)\n", X[i].re, X[i].im);
    }
    printf("\n");

    complex ShiftX[colums];
    fftshift(X, ShiftX, colums);
    printf("零频分量移到频谱中心 FFTShift:\n");
    for (int i = 0; i < colums; i++) {
        printf("(%f,%f)\n", ShiftX[i].re, ShiftX[i].im);
    }
    printf("\n");

    float PowerX[colums];
    powerSpectrum(ShiftX, PowerX, colums);
    printf("功率谱 powerSpectrum:\n");
    for (int i = 0; i < colums; i++) {
        printf("(%f)\n", PowerX[i]);
    }
    printf("\n");

}

 

运行结果

 

 

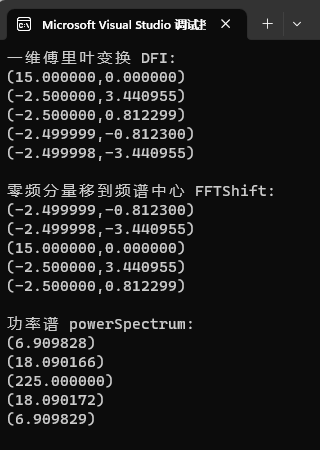
二维傅里叶功率谱的计算

#include <stdio.h>
#include <math.h>

#define pi 3.1415926
#define rows 3
#define colums 5

typedef struct {
    float re;// really 
    float im;// imaginary 
}complex, * pcomplex;

complex complexadd(complex a, complex b) //复数加
{
    complex rt;
    rt.re = a.re + b.re;
    rt.im = a.im + b.im;
    return rt;
}

complex complexMult(complex a, complex b) //复数乘
{
    complex rt;
    rt.re = a.re * b.re - a.im * b.im;
    rt.im = a.im * b.re + a.re * b.im;
    return rt;
}

/// <summary>
/// 二维离散傅里叶变换
/// </summary>
/// <param name="f">时域数据</param>
/// <param name="F">频域数据</param>
/// <param name="R">行数</param>
/// <param name="C">列数</param>
void dft2d( complex f[][colums], complex F[][colums], int R, int C)
{
    complex temp;
    int k, n, i, j;
    for (i = 0; i < R; i++) {
        for (j = 0; j < C; j++) {
            F[i][j].re = 0;
            F[i][j].im = 0;
            for (k = 0; k < R; k++) {
                for (n = 0; n < C; n++) {
                    double rad = ((double)i * k * C + (double)j * n * R) / ((double)R * C);
                    temp.re = (float)cos(2 * pi * rad);
                    temp.im = -(float)sin(2 * pi * rad);
                    F[i][j] = complexadd(F[i][j], complexMult(f[k][n], temp));
                }
            }
        }
    }
}
/// <summary>
/// 二维离散傅里叶逆变换
/// </summary>
/// <param name="F">频域数据</param>
/// <param name="f">时域数据</param>
/// <param name="R">行数</param>
/// <param name="C">列数</param>
void idft2d( complex F[][colums], complex f[][colums], int R, int C) 
{
    complex temp;
    int k, n, i, j;
    for (i = 0; i < R; i++) {
        for (j = 0; j < C; j++) {
            f[i][j].re = 0;
            f[i][j].im = 0;
            for (k = 0; k < R; k++) {
                for (n = 0; n < C; n++) {
                    double rad = ((double)i * k * C + (double)j * n * R) / ((double)R * C);
                    temp.re = (float)cos(2 * pi * rad);
                    temp.im = (float)sin(2 * pi * rad);
                    f[i][j] = complexadd(f[i][j], complexMult(F[k][n], temp));
                }
            }
            f[i][j].re /= R * C;
            f[i][j].im /= R * C;
        }
    }
}

/// <summary>
/// 将零频分量移到频谱中心
/// </summary>
/// <param name="F">频域数据</param>
/// <param name="Shift">零频分量移到频谱中心的数据</param>
/// <param name="R">行数</param>
/// <param name="C">列数</param>
void fftshift2(complex F[][colums], complex Shift[][colums], int R, int C) {
    for (int i = 0; i < R; i++) {
        for (int j = 0; j < C; j++) {
            int shiftIndexC = (j + (C - 1) / 2 + 1) % C;
            int shiftIndexR = (i + (R - 1) / 2 + 1) % R;
            Shift[i][j] = F[shiftIndexR][shiftIndexC];
        }
    }
}
/// <summary>
/// 计算功率谱函数
/// </summary>
/// <param name="F">零频分量移到频谱中心的数据</param>
/// <param name="P">功率谱数据</param>
/// <param name="R">行数</param>
/// <param name="C">列数</param>
void powerSpectrum2d(complex F[][colums], float P[][colums], int R, int C) {
    for (int i = 0; i < R; i++) {
        for(int j = 0; j < C; j++)
            P[i][j] = F[i][j].re * F[i][j].re + F[i][j].im * F[i][j].im;
    }
}

int main() {
    complex X2d[rows][colums], x2d[rows][colums];
    complex samples2d[rows][colums] = { {{1,0}, {2,0}, {3,0}, {4,0}, {5,0}},
                                        {{2,0}, {2,0}, {1,0}, {4,0}, {5,0}},
                                        {{1,0}, {2,0}, {8,0}, {4,0}, {5,0}}, };

    dft2d(samples2d, X2d, rows, colums);
    printf("二维傅里叶变换 2D DFI:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < colums; j++) {
            printf("(%f,%f)\t", X2d[i][j].re, X2d[i][j].im);
        }
        printf("\n");
    }
    printf("\n");

    complex ShiftX2d[rows][colums];
    fftshift2(X2d, ShiftX2d, rows, colums);
    printf("零频分量移到频谱中心 FFTShift:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < colums; j++) {
            printf("(%f,%f)\t", ShiftX2d[i][j].re, ShiftX2d[i][j].im);
        }
        printf("\n");
    }
    printf("\n");

    float PowerX2d[rows][colums];
    powerSpectrum2d(ShiftX2d, PowerX2d, rows, colums);
    printf("功率谱 powerSpectrum:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < colums; j++) {
            printf("(%f)\t", PowerX2d[i][j]);
        }
        printf("\n");
    }
    printf("\n");
 
}

运行结果

 

 

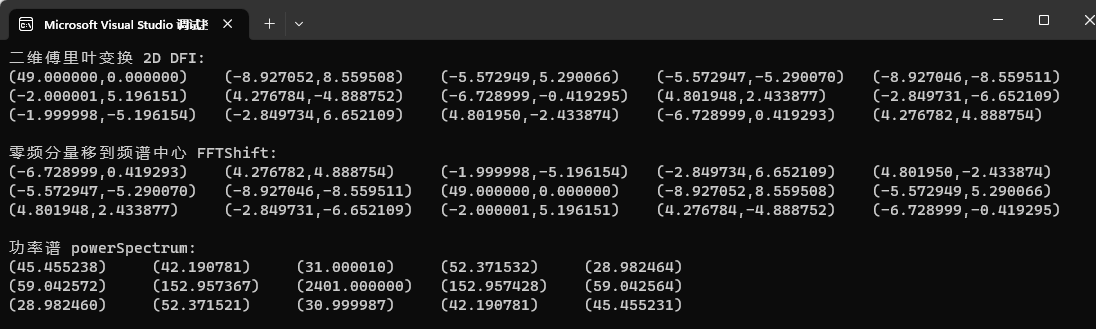
 假设绿色框内的数据傅里叶变换后的数据ShiftX2d，将ShiftX2d作为一个周期T，在其上边左边左上角分别复制。红框取一个周期T数据，就得到了零分量频率放到中心的频谱。