Floyd算法学习笔记

Floyd算法

这是最简单 码量最低 最无脑我们学的第一个最短路径算法。

他的本质其实是动态规划。万恶的 \(DP\) !

要想求任意两点最短路，我们就要把它存储起来（废话），由于 \(Floyd\) 的运算方法的特性，必须用邻接矩阵来储存。讲句废话，邻接矩阵的储存方法是如果 \(i \to j\) 之间有一条边，则 f[i][j] 表示距离，否则初始化为无穷大，比如 2147483648 0x3f3f3f3f 之类的。

方法

核心就是“三角不等式”——也就是说，如果绕路要比直接走近，那么就绕路。注意，这里的直接走并不仅仅是指走直线，它也可能是绕路更新以后变成当前的“直线”距离的。

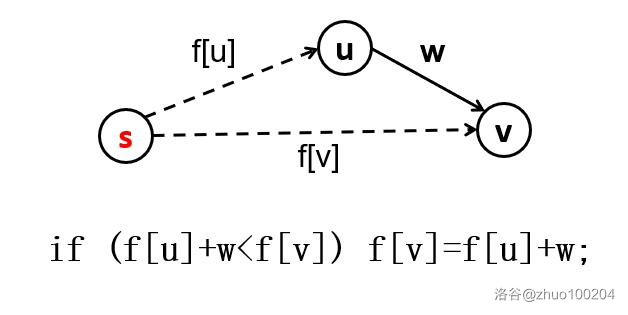
那么，具体我们应该怎样实现呢？必须遵循一定的规律。考虑到 \(DP\) 是具有“阶段”这个概念的，对于这个算法也一样。枚举每一个点，然后看两个点之间经过这个点会不会更短。具体代码就是这样：

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			d[i][j]=min(d[i][j],d[i][k]+d[k][j]);

因此，这种算法的时间复杂度为 \(O(n^3)\)。似乎效率较为低下，但是其实不然，因为：

• \(Floyd\) 求出的是任意两点间的最短路。\(Dijkstra\) 和某种死了的算法都只能求出“单源最短路”。

• \(Floyd\) 的一个性质是“传递闭包”。在解决某些看似与最短路毫无关系的问题时，这个性质却经常有很大的用处。

模板代码

以B3647 【模板】Floyd为例

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int a[N][N];
int n,m;
int main(){
	cin>>n>>m;
	memset(a,0x3f,sizeof(a));
	for(int i=1;i<=n;i++)a[i][i]=0;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		a[u][v]=a[v][u]=min(a[u][v],w);
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++) cout<<a[i][j]<<" ";
		cout<<endl;
	}
}

应用 1：传递闭包

比较常见的例子有P1037 [NOIP2002 普及组] 产生数。

这个题让人一眼就想到了 \(DFS\)。遗憾的是，这种情况下搜索会非常耗时，于是就会非常影响心情。对此我们可以用 \(Floyd\) 的传递闭包性质，在这里也就是说，假如 \(a \to b\) 和 \(b \to c\) 都是可行的，那么 \(a \to c\) 也是可行的。这就是所谓的传递性。这里我们只需要对弗洛伊德的模板算法略加修改，就可以得到正解。

for(int k=1;k<=n;k++){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			a[i][j]=a[i][j]||(a[i][k]&&a[k][j]);
		}
	}
}

这样我们就能找到每一个数的变化方式，最后根据乘法原理，把他们都乘起来就可以了。代码：

点击查看代码

#include<bits/stdc++.h>
#define very_long __uint128_t
using namespace std;
const int N=110;
bool a[N][N];
int s[N];
void put_vl(__uint128_t a){
	if(a>9) put_vl(a/10);
	putchar(a%10+'0');
}
int wei(int x){
	int tot=0;
	do{
		tot++;
	}while(x=x/10);
}
unsigned long long int m;
very_long ans=1;
string n;
int main(){
	cin>>n>>m;
	memset(a,0,sizeof(a));
	for(int i=0;i<=9;i++)a[i][i]=1;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		a[u][v]=1;
	}
	for(int k=0;k<=9;k++){
		for(int i=0;i<=9;i++){
			for(int j=0;j<=9;j++){
				a[i][j]=(a[i][k]&&a[k][j])||a[i][j];
			}
		}
	}
	for(int i=0;i<=9;i++){
		for(int j=0;j<=9;j++)s[i]+=a[i][j];
	}
	int cnt=n.size();
	while(cnt--)ans*=s[n[cnt]-'0'];
	put_vl(ans);
}

（__uint128_t是一种非常大的整数。由于积可能很大，必须用uint128或者是干脆用高精度）

应用 2：k条边的最短路

有些时候，我们希望找到一条最短路径，但是我们有些时候需要找到的是要“经过 \(k\) 条边”的最短路径。这个时候，原来的算法就不好用了。然而我们依然可以通过这个思路，定义一个数组 c，c[k][i][j] 表示经过 \(i\) 条边的最短路即可。我们发现，这个过程类似于乘法，因为它是满足结合律的。这也就是说，我们可以把快速幂集成到这里。这样的话，整个过程的时间复杂度就是 \(O(n^3log k)\)。我们以P2886 [USACO07NOV] Cow Relays G为例来展示一下代码。注意，这道题的不同之处在于，点的“编号”会达到 5000，但是实际的“数量”却仅仅是 200。因此我们需要用到离散化——也就是说把点进行编码，否则会超时。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
struct matrix{
	int x[201][201];
}d;
int n,t,s,e;
bool vis[1001];
int nm[1001],tot;
matrix operator *(matrix A,matrix B){
	matrix C;
	memset(C.x,0x3f,sizeof(C.x));
	for(int k=0;k<tot;k++)
		for(int i=0;i<tot;i++)
			for(int j=0;j<tot;j++)	C.x[i][j]=min(A.x[i][k]+B.x[k][j],C.x[i][j]);
	return C;
}
matrix Fast(matrix A,long long n){
	matrix S=A;
	n--;
	while(n){
		if(n&1){
			S=S*A;
		}
		A=A*A;
		n=n>>1;
	}
	return S;
}
int main(){
	cin>>n>>t>>s>>e;
	memset(d.x,0x3f,sizeof(d.x));
	for(int i=0;i<t;i++){
		int u,v,w;
		cin>>w>>u>>v;
		if(!vis[u])vis[u]=1,nm[u]=tot++;
		if(!vis[v])vis[v]=1,nm[v]=tot++;
		d.x[nm[u]][nm[v]]=d.x[nm[v]][nm[u]]=w;
	}
	d=Fast(d,n);
	cout<<d.x[nm[s]][nm[e]]<<endl;
}