人工智能系统

什么是人工智能系统，人工智能系统和传统系统最大的区别在于规则是否明确，传统系统是根据程序员确定的规则去执行某些操作，这些规则都是已知的，但是在现实生活中，很多规则都是未知的，规则即规律，传统系统无法根据数据来自己总结出一个规律出来需要人工干预，而当数据量过于庞大时，人工也很难总结出某种规律，人工智能系统解决这类问题的核心方法就是机器学习，让系统可以自己通过数据总结出规律，这样就知道了某种数据的相关性模型，之后再输入同种的数据，系统就能根据规律得出相应的结果，对于简单的可以通过机器学习，而复杂一点的需要强化学习。

特性维度	传统系统 (基于规则/逻辑)	人工智能系统 (基于数据/学习)
核心原理	确定性逻辑与规则	概率性统计与模式匹配
知识来源	人类专家领域知识，被编码成明确的规则(if-else)	海量的训练数据，系统从中自行发现规律和模式
构建方式	自上而下的设计。程序员手动编写所有逻辑和决策流程。	自下而上的学习。程序员设计模型结构，由数据驱动模型参数的生成。
输出特点	确定性、可预测。相同的输入必定产生相同的输出。	概率性、有容错性。相同的输入可能产生相似但不完全相同的输出（生成式AI），输出是一个概率分布。
灵活性/泛化能力	脆弱。只能处理规则预先定义好的情况，对未知或边缘情况束手无策。	强大。能够处理训练时未曾见过的新数据（泛化能力），适应变化的环境。
可解释性	高。决策过程清晰可追溯，可以一步步调试。	低（常被称为“黑盒”）。很难解释为什么模型会做出某个特定决策，通常只知道它“有效”。
优势	逻辑透明、结果稳定、计算高效、在定义明确的领域非常可靠。	能解决复杂、模糊的问题（如图像识别、自然语言），自动化程度高，能发现人类未察觉的深层规律。
劣势	无法处理规则未定义的复杂、模糊问题，维护和扩展规则库成本极高。	需要大量高质量数据，训练成本高，决策不可控，可能存在数据偏见。

机器学习的一般流程

特征信息的提取是最为关键的，我们称之为特征工程，现在最大的问题的是高级语义和低层特征之间的转换，首先人们对于文本和图像的理解无法从字符串或字符串的底层特征获取，像这种非结构化的数据

计算机两大语义表示形式

局部表示：一个词就是一个独立的符号，其含义是孤立且预设的，与其他词无关（如词典中的每个词条）。

分布式表示：：一个词的含义由其上下文伙伴共同定义，并被表示为一個稠密向量，语义相近的词在向量空间中也彼此靠近。

特性	局部表示	分布式表示
核心思想	一个符号，一个含义	一个词由其上下文定义
代表形式	One-hot 向量	Word2Vec, GloVe, BERT 等生成的词向量
向量维度	高维（等于词汇表大小）	低维（如50, 100, 300维）
向量密度	稀疏（绝大部分元素为0）	稠密（绝大部分元素为非零实数）
语义关系	无法捕获（所有向量两两正交）	自动捕获（相似词距离近）
可计算性	无	支持向量运算（如 国王 - 男人 + 女人 ≈ 女王）
可解释性	强（每个ID对应一个确切的词）	弱（每个维度的含义不明确）
主要应用时代	传统NLP方法	现代深度学习NLP的基石

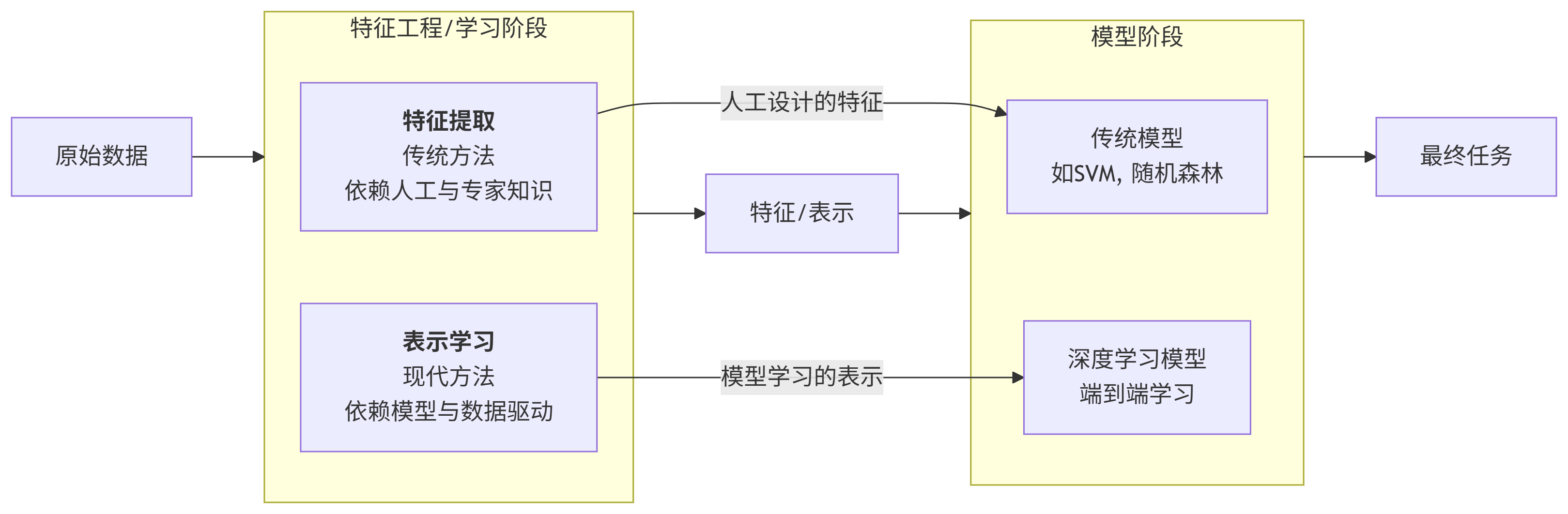
特征提取和表示学习的区别：

特征提取是人为告诉机器哪些特征可能有用，基于任务或先验对去除无用特征

表示学习是让机器自己从数据中摸索和发现哪些特征有用，通过深度模型学习高层语义特征

关键在于人工干预占比是否大，表示学习是当前人工智能发展的主流，因为它能自动化地发现那些人类专家也难以设计的复杂、抽象特征，极大地推动了图像、语音、自然语言处理等领域的进步

表示学习的一般流程

二者的比较

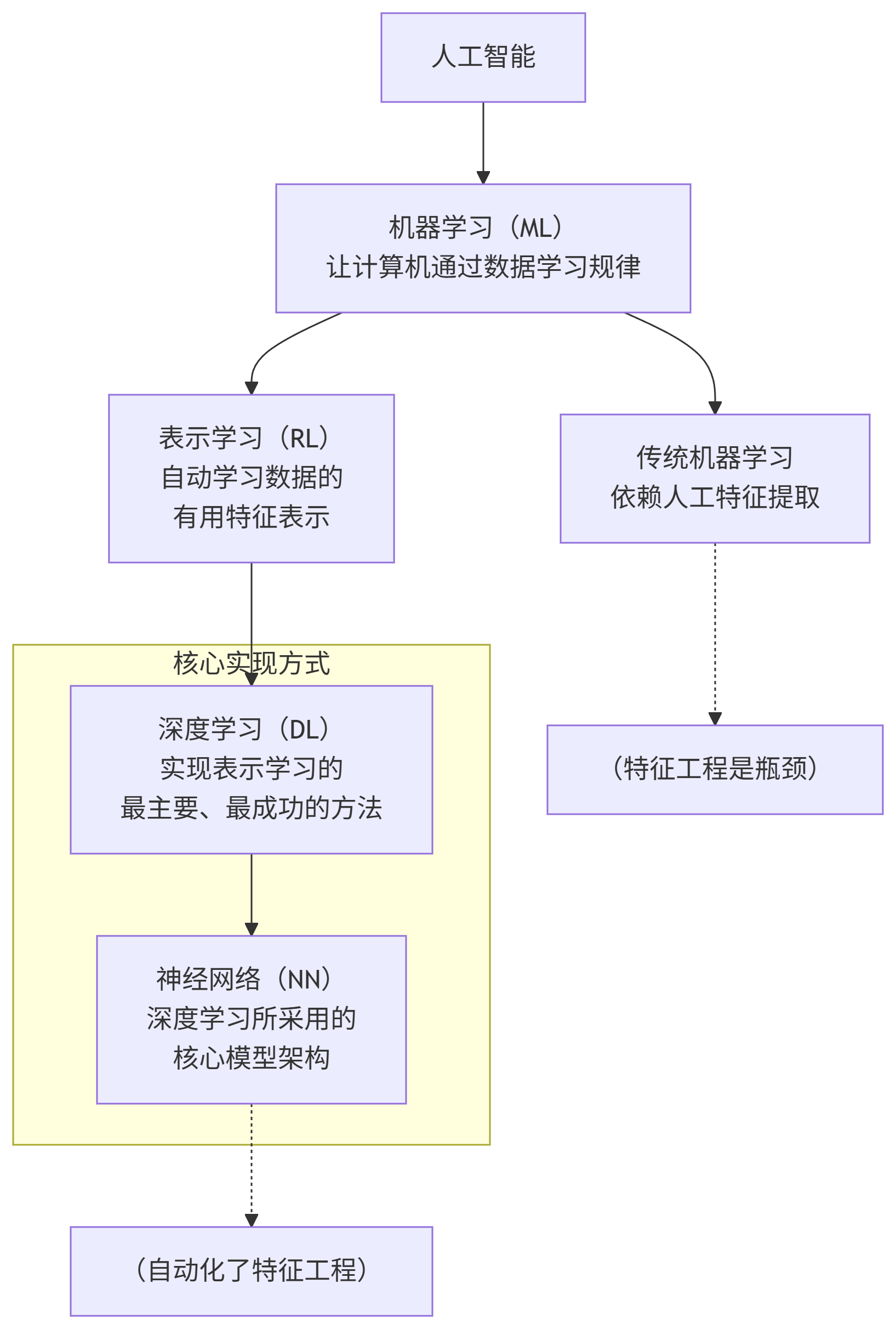
人工智能、机器学习、表示学习、深度学习和神经网络的关系

人工智能系统的主要实现方法是机器学习。在传统机器学习中，特征工程往往依赖人工设计，而表示学习则致力于将这一过程自动化，使模型能够自主地从原始数据中学习有效的特征表示。由于高级语义信息难以通过少数几层网络有效捕获，因此通常需要引入更多层次进行逐级特征提取。数据从输入层到输出层的传递过程中，每一层都会自动进行特征变换与表示学习，逐步从低级特征中提炼出更抽象的高级特征。浅层网络通常捕获局部、底层的模式（如边缘、纹理），而深层网络则负责识别全局、高级的语义结构（如物体部件、整体形态）。

随着网络层数的增加，模型能够学习到更加复杂的特征表示，这种多层次的、端到端的特征学习机制称为深度学习。然而，网络越深，模型的复杂度越高，不同层所学习特征对最终结果的贡献也越难以直观解释。每层特征如何影响模型输出，即其与预测结果之间的关联强弱，成为一个关键问题。神经网络通过多层互联的简单计算单元（神经元）以及可调整的连接权重，来模拟复杂的函数映射关系。权重的优化过程实际上间接决定了每一层特征的贡献程度，从而实现对高阶语义的逐步抽象与有效识别。

最后说一下我们现在常说的大模型和这些关系是什么

机器学习的一般流程始于数据准备阶段，该阶段需明确特征（自变量） 与对应的目标值或因变量（也称标签或结果）。随后，通过特定的学习算法，从数据中拟合出特征与目标之间的映射关系，即得到一个函数形式的关系：f(特征) ≈ 结果。

这个通过数据学习得到的函数 f，即是我们所称的模型，其本质是输入空间到输出空间的一种映射。

以数学中的简单线性回归为例：假设已知两个数据点 (x₁, y₁), (x₂, y₂)，其中 x₁, x₂ 是特征，y₁, y₂ 是对应的结果。通过“学习”（在这里即最小二乘法拟合），我们可以获得一条穿过这两点的直线方程 y = wx + b，其中 w 和 b 是学习得到的参数。这条直线方程即为所得的模型。

训练完成后，若输入一个新的特征值 x₃，即可利用该模型计算出预测结果 ŷ₃ = w · x₃ + b。

需要补充的是，现实世界中的机器学习问题往往远较此复杂：数据点通常远多于两个（常用大规模数据集），特征维度更高（多元问题），且变量间关系也远非线性那么简单（可能需神经网络等复杂模型刻画）。但其核心思想与上述线性例子一脉相承：基于已知数据学习一个映射函数 f，以期对新的输入做出准确预测。