CF1497C1 k-LCM (easy version)&&CF1497C2 k-LCM (hard version)

找规律题，神奇的是题解说样例把所有的情况都点出来了，而我都ac了，才看到这条。

 

 

 我的敏感性终于上来了吗？

看到lcm不超过n/2的时候我想到了可以试一下设可能的一个数字为n/2；

然后..突然想到n/2,n/4,n/4。

然后我就开始对n%4的各种情况进行讨论，发现没法构造出上面那么好看的答案了。

然后我就开始分奇偶。

发现奇数可以转化成偶数处理，-1然后再对半分即可。

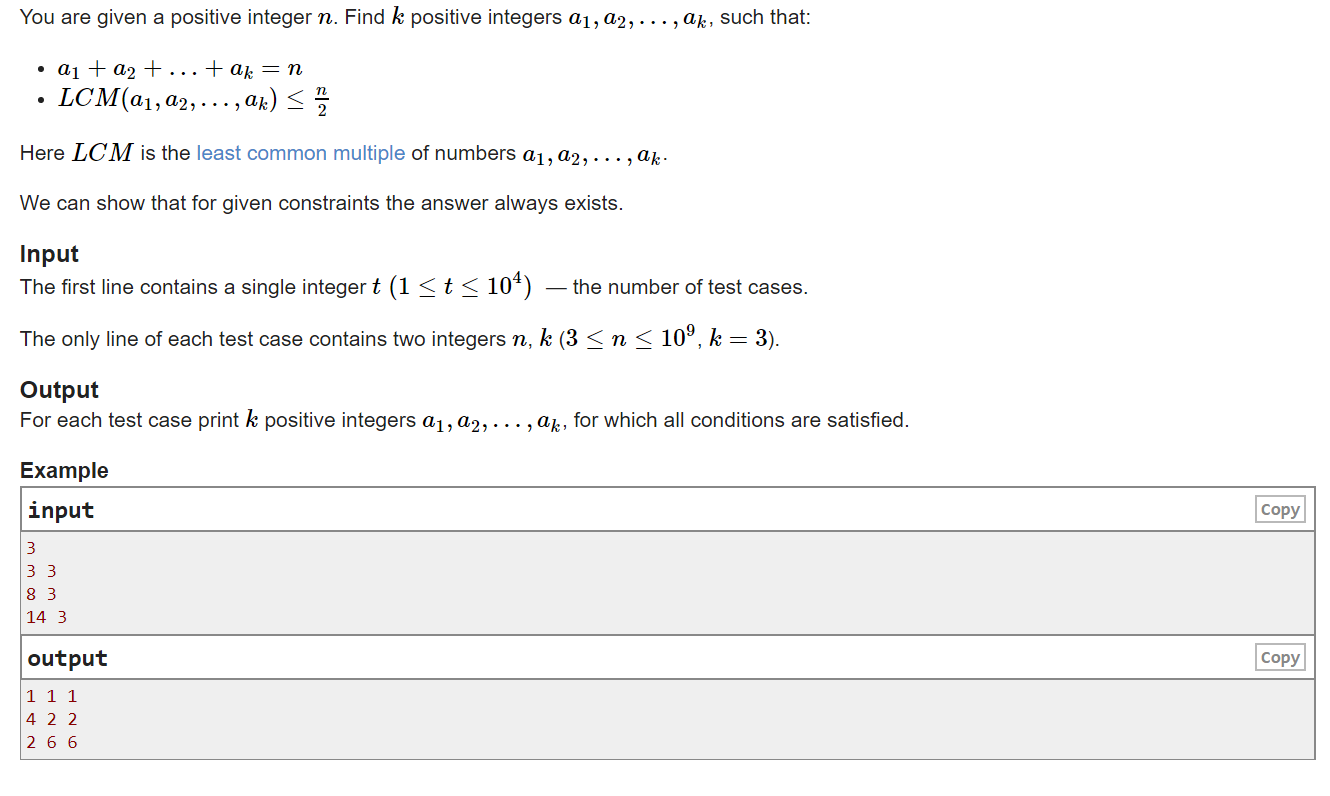
对于是偶数，但又不能被4整除的话，比如14，可以拆成2，6，6；

再比如18，可以拆成2，8，8；

这个多模拟几个数字就能发现了。

那么c1就解决了。

 

 

 

--------

以下是c1和c2的梦幻联动

一看c2样例，发现那么多个1，猜测当k大到一定数字之后，肯定是由1，1，1这种形式来凑。

跑步的时候想了很多，早上起来又想了很多，出发点都是1必能占一个坑位且不影响lcm，可以由2和1的组合构造出lcm必为偶数的情况。

one thousand years later

在wa了无数次后

我决定输出k-3个1，然后把c1的程序copy过来

a了。。。

 

-------

评论区有个外国孩子说，如果没有神奇数字k=3的话，c2会是非常难的一题，甚至可以压轴了。

对...就好比以前做高考数学。

 

------

不管怎么说，自己做出来的第一个c，以及比较有趣的思维题，很弱的李一水也还活着。