快速排序

快速排序能够实现原址排序，而且平均性能很好。最基本的快速排序基于分治思想。

算法过程

1. 选定分界值，将原数组划分为两个部分

2. 左边的值都小于分界值，右边的值都大于等于分界值

3. 对左右两侧数组再次进行1、2步骤

4. 直到所有数据排序完成

伪代码

QUICKSORT(A,low,high)
if low < high
	q = PARTITION(A,low,high)
	QUICKSORT(A,low,q-1)
	QUICKSORT(A,q+1,high)
	
PRTITION(A,low,high)
x = A[high]
i = low-1
for j=low -> high-1
	if A[j] <= x
		i++
		exchange A[i] with A[j]
exchange A[i+1] with A[high]
return i+1

划分(PARTITION)

• 选定一个分界值x（此例中为数组最后一个元素）

• 整个数组分为三个部分：

  • 小于x的部分

  • 大于等于x的部分

  • 未确定的部分

    

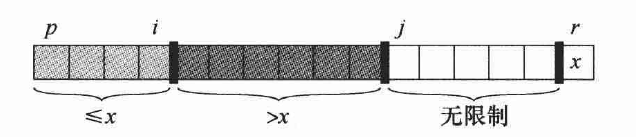
• 循环开始时i=low-1,j=low

• 考虑当前A[j]与分界值x的大小关系

  • 如果A[j]小于x，则i++，同时交换A[i]和A[j]\(\implies\)保证i之前为小于x的值
  • 否则j++，继续遍历

• 最后交换A[i+1]和x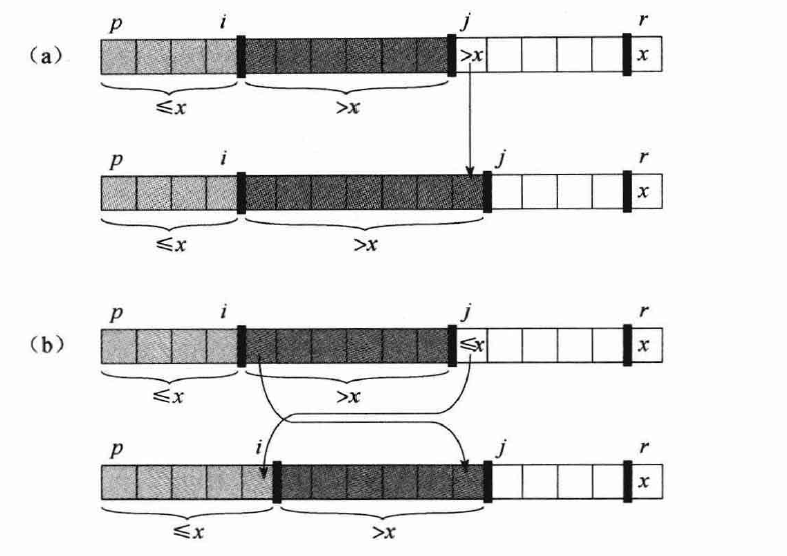

  

代码

void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

int partition(int *A, int low, int high)
{
    int x = A[high];
    int i = low - 1;
    for (int j = low; j <= high - 1; j++)
    {
        if (A[j] <= x)
        {
            i++;
            swap(&A[i], &A[j]);
        }
    }
    swap(&A[i+1], &A[high]);
    return i+1;
}

void quicksort(int *A, int low, int high)
{
    if (low < high)
    {
        int q = partition(A, low, high);
        quicksort(A, low, q - 1);
        quicksort(A, q + 1, high);
    }
}

随机化版本

输入的数组的元素分布不一定是均衡的，采用随机取样的方法期望在平均情况下划分是比较均衡的。

#include <iostream>
#include <ctime>
#include <cstdlib>

using namespace std;

//随机选择一个分界值
int random(int low, int high)
{
	srand(1);
	int len = high - low + 1;
	return rand() % len + low;
}

void swap(int* a, int* b)
{
	int temp = *a;
	*a = *b;
	*b = temp;
}

int partition(int* A, int low, int high)
{
	int i = low - 1;
	int x = A[high];
	for (int j = low; j < high; j++)
	{
		if (A[j] <= x)
		{
			i++;
			swap(&A[i], &A[j]);
		}
	}
	swap(&A[i + 1], &A[high]);
	return i + 1;
}

int random_partition(int* A, int low, int high)
{
	int i = random(low, high);
    //将分界值交换到最后一位
	swap(&A[high], &A[i]);
	return partition(A, low, high);
}

void random_quicksort(int* A, int low, int high)
{
	if (low < high)
	{
		int q = random_partition(A, low, high);
		random_quicksort(A, low, q - 1);
		random_quicksort(A, q + 1, high);
	}
}

快速排序的性能

快速排序的运行时间依赖于划分是否平衡，平衡与否依赖于划分的元素。

划分的复杂度

\[T(n)=\Theta(n)\\ n=high-low+1 \]

最坏情况分析

利用代入法证明\(T(n)=O(n^2)\)

\(T(n)=T(q)+T(n-q-1)+\Theta(n)\)

当\(q=0\)时，为最坏情况

即\(T(n)=T(0)+T(n-1)+\Theta(n)=T(n-1)+\Theta(n)\)

猜想\(T(n)=O(n^2) \to T(n)\le cn^2\)

当\(n=1\)时，成立

假设\(n=k\)时，\(T(k)=T(k-1)+\Theta(k)\le c_1k^2\)

当\(n=k+1\)时，

\(T(k+1)=T(k)+\Theta(k+1)=T(k-1)+\Theta(k)+\Theta(k-1)=T(k-1)+\Theta(k)\)

\(\therefore 存在c_2使得T(k+1)\le c_2k^2\)

\(\implies T(n)=O(n^2)\)

期望运行时间