Acwing 846. 树的重心(DFS枚举删除每一个点)

地址：https://www.acwing.com/problem/content/848/

 

解析：

y总先写的是一个无关重心的一个解法。即枚举每一个点，删掉它后，得出的剩余各个连通块中点数的最大值。

一：存图

邻接表，依然是熟悉的单链表，这里有多个单链表，也就是多个-1点，所以要全初始化为-1

无向图，来去各存一次，所以开两倍的e[]和ne[]

二：DFS

 

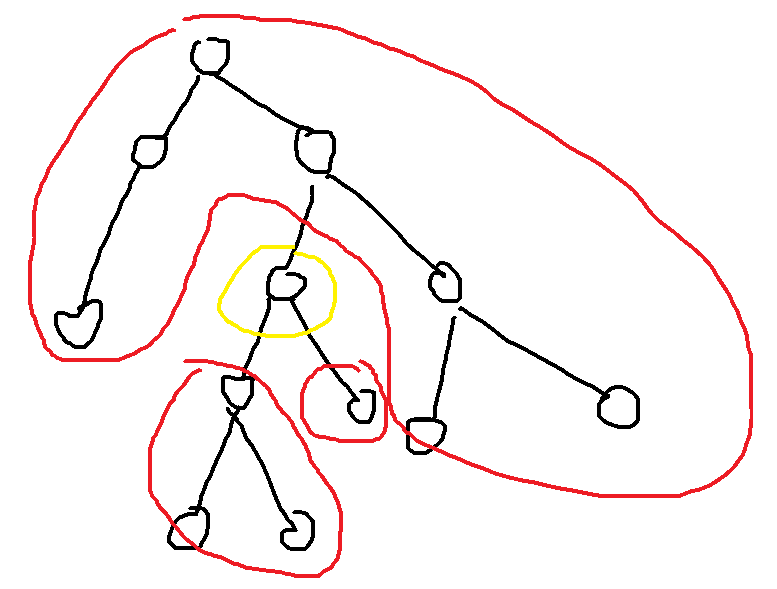
假设我们要删图中被标记的黄色点，发现，连通块来自于两部分：1.总点数-去掉它和它的子树  2.它的子树(不算本身)

所以每次，这两者取一个max，就是去掉黄色点后的连通块最大值

求1，需要以黄色点为根节点的子树总大小(算它本身)，求2，需要除黄色点以外的每个子树的大小。

看注释：

int dfs(int u)
{
    st[u]=true;//标记被访问
    int sum=1,res=0;//sum代表以u为根节点的子树大小，res表示去掉u后的连通块最大值
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];//得到点
        if(!st[j])
        {
            int s=dfs(j);//返回子树大小
            sum+=s;//得到u为根节点的子树大小
            res=max(res,s);//更新最大值，即删u后的子树大小
        }
    }
    res=max(res,n-sum);//n-sum，以外的连通块
    minn=min(minn,res);//更新总体最小值
    return sum;
}

 三：总的代码

#include<iostream>
#include<cstdio>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn = 1e5+10;
int h[maxn],ne[maxn*2],e[2*maxn],idx;
int n;
int minn=maxn;
bool st[maxn];
void add(int a,int b)
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
int dfs(int u)
{
    st[u]=true;
    int sum=1,res=0;
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!st[j])
        {
            int s=dfs(j);
            sum+=s;
            res=max(res,s);
        }
    }
    res=max(res,n-sum);
    minn=min(minn,res);
    return sum;
}
int main()
{
    memset(h,-1,sizeof(h));
    memset(st,false,sizeof(st));
    cin>>n;
    for(int i=1;i<n;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b);
        add(b,a);
    }
    dfs(1);
    cout<<minn<<endl;
}