Acwing 143. 最大异或对(字典树+贪心)

地址：https://www.acwing.com/problem/content/145/

没买课的话，应该打不开题。我就截个图吧，题意是很简单的。

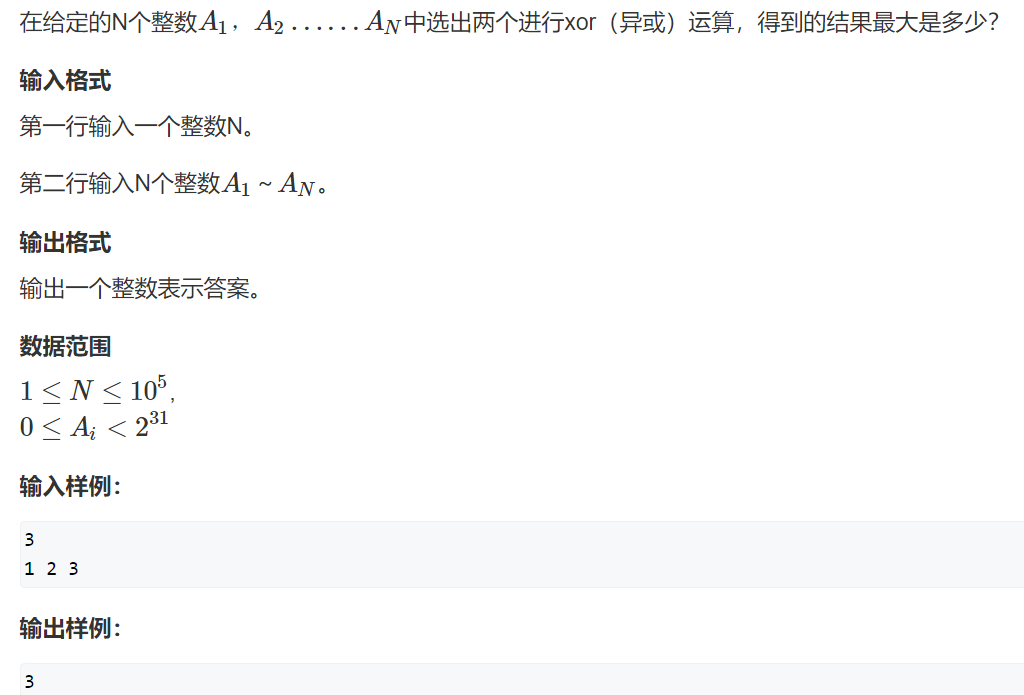
解析：

关于位运算，我有个小笔记可供参考：https://www.cnblogs.com/liyexin/p/13914911.html

1：贪心思路

首先明确，什么是异或运算，两个数不同，则为1，否则为0。

给定ai，如果想让ai和一个数的异或结果最大，很明显，要从高位开始看，尽量从高位筛选同位不同数的数字。

举个例子：

10：1010

x

从高位(第3位)开始看，10的第三位为1，最优解是x的第三位与它不同，为0。10的第二位为0，最优解是x的第二位为1......以此类推。

这就是贪心的思路。

2：字典序优化

怎么优化呢？暴力跑的话是n*n。

发现每个数字化为二进制的话，按题中范围最大为31位。直接跑字典序的话，复杂度可以优化到n*31

如图所示：

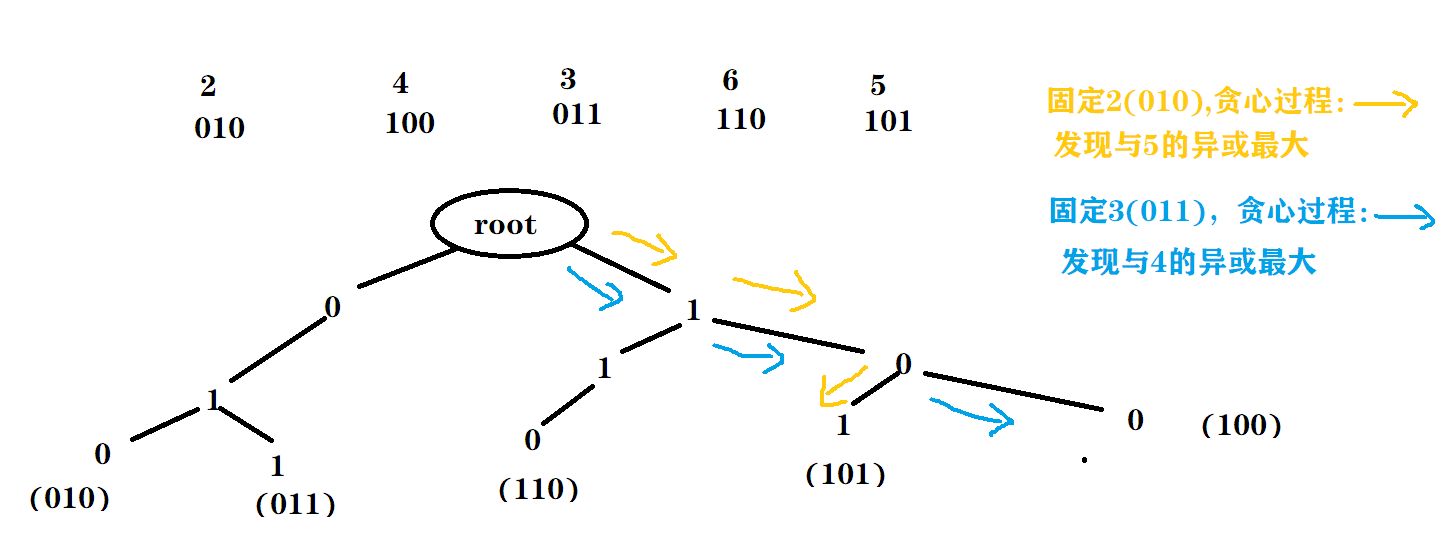
总结一下，对于当前的二进制位，如果存在与它不同的，就走过去，否则，只能沿着仅存的那条路走了。

由于N是1e5，假设每个数都有31位而且都占有新节点，那么最多一共需要N*31个节点位，即要开到son[N*31][31]

代码:

#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
const int maxn=1e5+10,maxn2=31*maxn;
int idx=0;
typedef long long ll;
int a[maxn];
int son[maxn2][2];
void insert(int x)
{
    int p=0;
    for(int i=30;i>=0;i--)
    {
        int u = x>>i&1;
        if(!son[p][u])
            son[p][u]=++idx;
        p=son[p][u];
    }
    return ;
}
int query(int x)
{
    int res=0;
    int p=0;
    for(int i=30;i>=0;i--)
    {
        int u=x>>i&1;
        if(son[p][!u])
        {
            res=res*2+1;
            p=son[p][!u];
        }            
        else
        {
            p=son[p][u];
            res=res*2;
        } 
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        insert(a[i]);
    }
    int maxx=0;
    for(int i=1;i<=n;i++)
    {
        maxx=max(maxx,query(a[i]));
    }
    cout<<maxx<<endl;
    return 0 ; 
}