04-树
1.学习总结
树结构思维导图
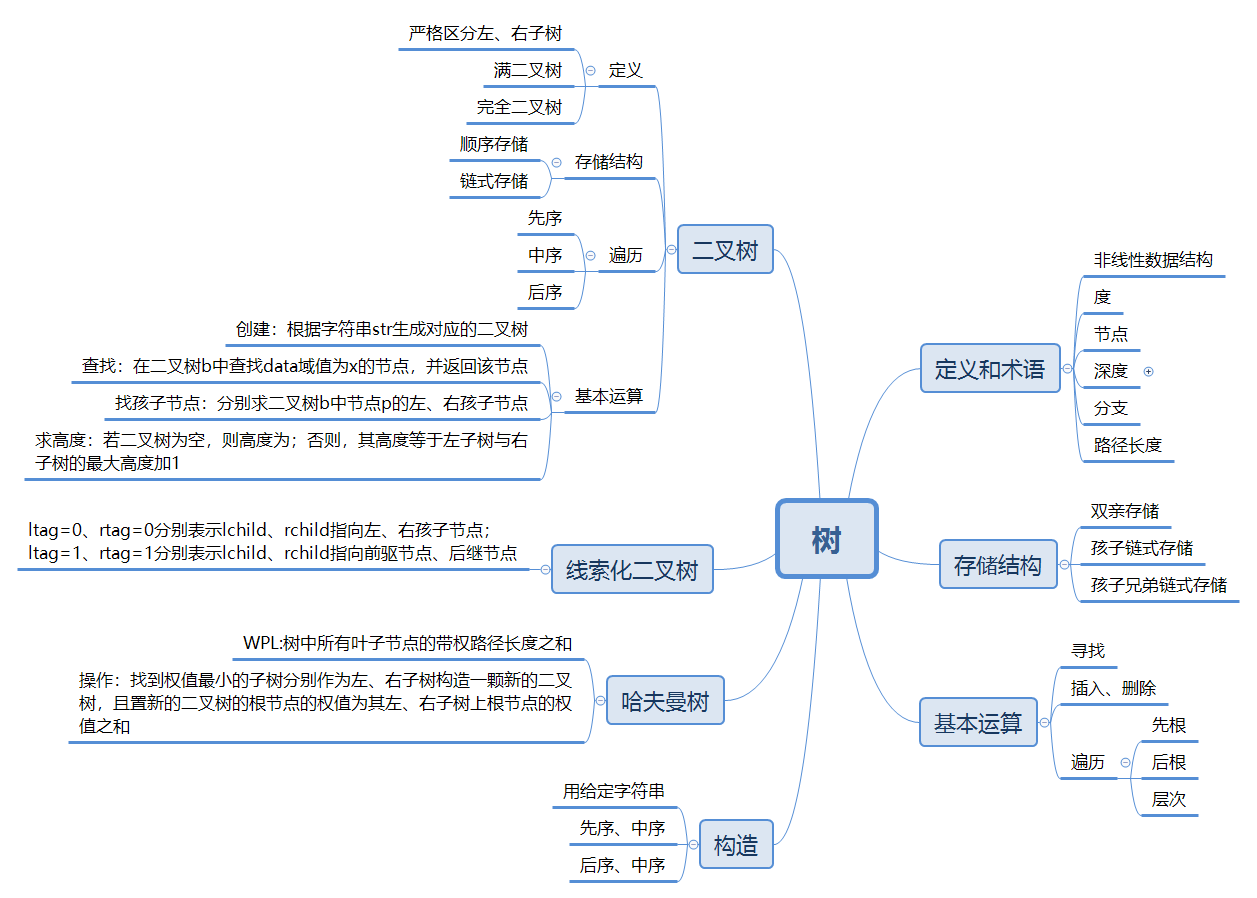
1.2树结构学习体会
我觉得树这部分还挺难的,不过挺有意思的,我会继续好好学习的!
大部分操作系统的目录结构就是采用树结构。
树的种类有很多,树所扩展出来的很多数据结构都有着很大的作用。
2.PTA实验作业
2.1题目一:6-1 jmu-ds-二叉树操作集
2.2设计思路
根据层次字符序列创建二叉树
void CreateBTree(BTree &BT,string str)
{
定义一个队列q1
定义一棵树T
定义变量i
if 字符串首个是‘#’
T为空树
else 为T创建一个新节点
T->data=str[0]
T入队
while(q1不为空&&str[i]不为空)
{
取队首元素赋给t,并出队
i++
if str[i]等于‘#’
t的左孩子为空
else 为左孩子创建节点并赋值
将该节点入队
i++
if str[i]等于‘#’
t的右孩子为空
else 为右孩子创建节点并赋值
将该节点入队
}
}
2.1题目二:6-4 jmu-ds-表达式树
2.2设计思路
建表达式的二叉树
void InitExpTree(BTree &T,string str)
{
定义一个栈s存数字
定义一个栈op存操作符
定义变量i
把’#‘压入栈
while str[i]不等于’\0‘
if str[i]为运算符
判断其优先级
if 该操作符优先级比栈顶小
op入栈
if 该操作符优先级比栈顶大
创建新节点T并赋值
将栈顶元素赋给右孩子
s出栈
将栈顶元素赋给右孩子
s出栈
将新节点T入栈s
op出栈
if 该操作符的优先级与栈顶相等
op出栈
else 创建新节点T并赋值
将新节点左、右节点初始为空
将新节点T入栈s
while op栈顶元素不为’#‘
创建新节点T并赋值
将栈顶元素赋给右孩子
s出栈
if s不为空
将栈顶元素赋给左孩子
s出栈
将新节点T入栈s
op出栈
将s的栈顶元素赋给树根
计算表达式树
double EvaluateExTree(BTree T)
{
定义变量sum,m,n;
if 左、右子树为空
返回T的数值
递归调用EvaluateExTree,使m为左孩子,n为右孩子
switch T不为空
case’+‘:m+n
case’_':m-n
case'*':m*n
case‘/’:if n为0,退出
else m/n
}
2.3代码截图
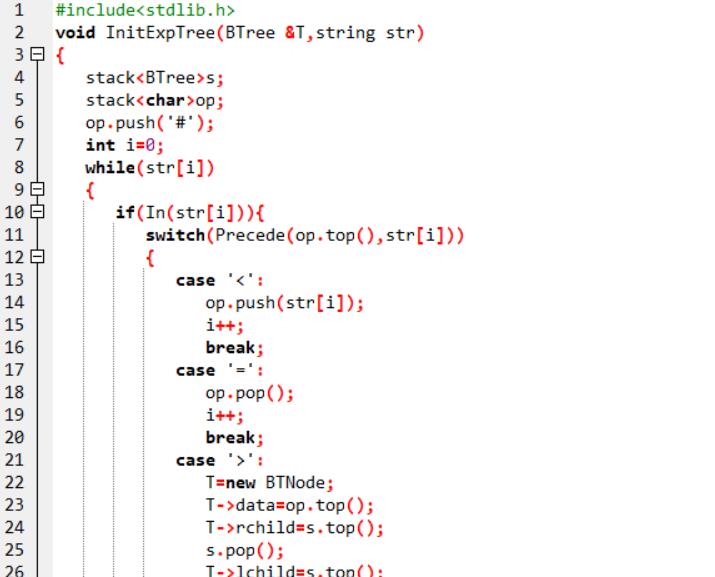
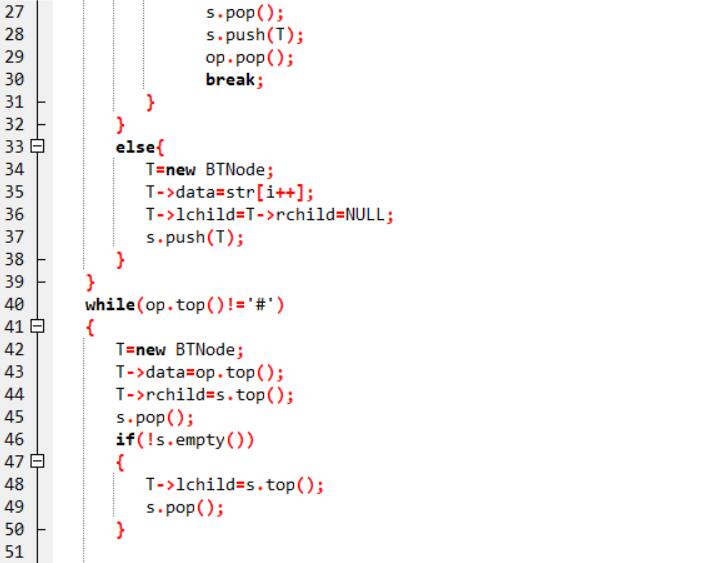

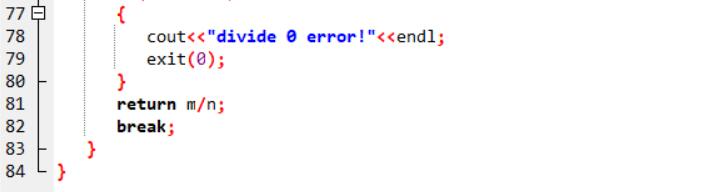
2.4PTA提交列表说明
前几次提交时,没考虑除数为零,后来改正了后又由于divide单词拼写错误出现了部分错误,改正后就对了。
2.1题目三:7-1 还原二叉树
2.2设计思路
重建二叉树
BinTree reCreate(char pre[],char in[],int len)
{
定义一棵树T
定义一个变量i
if len为0
则返回空
else 为T申请空间
T->data=pre[0]
for(i;i<len;i++)
{
if in[i]等于pre[0]
退出
}
T->Left = reCreate(pre+1,in,i)
T- >Right = reCreate(pre+i+1,in+i+1,len-i-1)
}
求二叉树的高度
int GetHeight( BinTree T )
{
定义两个数HL,HR;
if T等于NULL
返回
else HL = GetHeight(T->left);
HR = GetHeight(T->right);
返回 HL、HR中较大的数加一
}
}
2.3代码截图
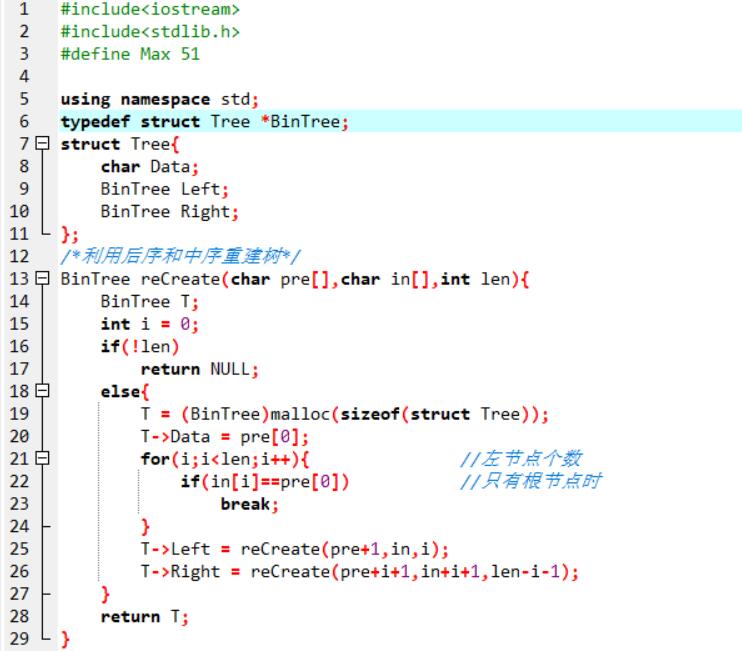

2.4PTA提交列表说明
第一次用C提交出现了错误;第二次提交时因为没有区分大小写出现了编译错误,改正后就正确了
3.截图本周题目集的PTA最后排名

3.3我的总分:230
4. 阅读代码
4.1代码地址:https://blog.csdn.net/shuangde800/article/details/7341289
4.2代码解析:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define N 10 // 带编码字符的个数,即树中叶结点的最大个数
#define M (2*N-1) // 树中总的结点数目
class HTNode{ // 树中结点的结构
public:
unsigned int weight;
unsigned int parent,lchild,rchild;
};
class HTCode{
public:
char data; // 待编码的字符
int weight; // 字符的权值
char code[N]; // 字符的编码
};
void Init(HTCode hc[], int *n){
// 初始化,读入待编码字符的个数n,从键盘输入n个字符和n个权值
int i;
printf("input n = ");
scanf("%d",&(*n));
printf("\ninput %d character\n",*n);
fflush(stdin);
for(i=1; i<=*n; ++i)
scanf("%c",&hc[i].data);
printf("\ninput %d weight\n",*n);
for(i=1; i<=*n; ++i)
scanf("%d",&(hc[i].weight) );
fflush(stdin);
}//
void Select(HTNode ht[], int k, int *s1, int *s2){
// ht[1...k]中选择parent为0,并且weight最小的两个结点,其序号由指针变量s1,s2指示
int i;
for(i=1; i<=k && ht[i].parent != 0; ++i){
; ;
}
*s1 = i;
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && ht[i].weight<ht[*s1].weight)
*s1 = i;
}
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && i!=*s1)
break;
}
*s2 = i;
for(i=1; i<=k; ++i){
if(ht[i].parent==0 && i!=*s1 && ht[i].weight<ht[*s2].weight)
*s2 = i;
}
}
void HuffmanCoding(HTNode ht[],HTCode hc[],int n){
// 构造Huffman树ht,并求出n个字符的编码
char cd[N];
int i,j,m,c,f,s1,s2,start;
m = 2*n-1;
for(i=1; i<=m; ++i){
if(i <= n)
ht[i].weight = hc[i].weight;
else
ht[i].parent = 0;
ht[i].parent = ht[i].lchild = ht[i].rchild = 0;
}
for(i=n+1; i<=m; ++i){
Select(ht, i-1, &s1, &s2);
ht[s1].parent = i;
ht[s2].parent = i;
ht[i].lchild = s1;
ht[i].rchild = s2;
ht[i].weight = ht[s1].weight+ht[s2].weight;
}
cd[n-1] = '\0';
for(i=1; i<=n; ++i){
start = n-1;
for(c=i,f=ht[i].parent; f; c=f,f=ht[f].parent){
if(ht[f].lchild == c)
cd[--start] = '0';
else
cd[--start] = '1';
}
strcpy(hc[i].code, &cd[start]);
}
}
int main()
{
int i,m,n,w[N+1];
HTNode ht[M+1];
HTCode hc[N+1];
Init(hc, &n); // 初始化
HuffmanCoding(ht,hc,n); // 构造Huffman树,并形成字符的编码
for(i=1; i<=n; ++i)
printf("\n%c---%s",hc[i].data,hc[i].code);
printf("\n");
return 0;
}
4.3实现功能:通过哈夫曼树来构造的编码称为哈夫曼编码。
5. 代码Git提交记录截图



 浙公网安备 33010602011771号
浙公网安备 33010602011771号