堆排序（heapsort）

	插入排序	归并排序
相同点	同样具有空间原址性，任何时候都只需要常数个额外的元素空间存储临时数据	时间复杂度都是O(nlgn)

 

“堆”的数据结构是一种算法设计技巧，堆不仅用在堆排序中，还可以构造一种有效的优先队列。

   

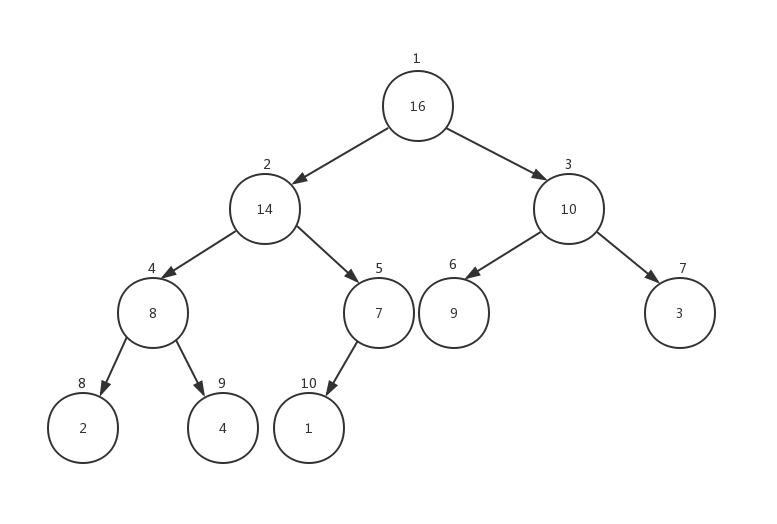
二叉堆是一个数组，表示堆的数组A包含两个属性，通常，0 <= A.size <= A.length，树的根节点是A[1],给定一个节点的下标，可以计算得到它的父节点、左孩子和右孩子的下标：

PARENT(i)	LFET(i)	RIGHT(i)
i >> 1	i << 1	i << 1 + 1

二叉堆可以分为两种形式：最大堆和最小堆。最大堆性质是除了根节点以外的所有节点i都要满足： 

A[PARENT(i)] >= A[i]；最小堆性质是指除了根以外的所有节点i都有： A[PARENT(i)] <= A[i]。

 

如果把堆看作一棵树，通常定义一个堆中节点的高度就为该节点到叶节点最长简单路径上边的数目；进而可以把堆的高度定位为根节点的高度。

既然一个包含n个元素的堆可看作一棵完全二叉树，那么该堆结构上的一些操作的运行时间至多与树的高度成正比，即时间复杂度为O(lgn)。

 

维护堆的性质：

    /**
     * 输入为一个数组和一个下标i，假定根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆，
     * 但这时elements[i]有可能小于其孩子，这样就违背了最大堆的性质，
     */
    private void maxHeapify(int[] elements, int i) {
        int n = elements.length;
        int l = LEFT(i);
        int r = RIGHT(i);
        int largest = i;
        if (l <= n && elements[l] > elements[i])
            largest = l;
        if (r <= n && elements[r] > elements[largest])
            largest = r;
        if (largest != i) {
            int temp = elements[i];
            elements[i] = elements[largest];
            elements[largest] = temp;
            maxHeapify(elements, largest);
        }
    }

建堆：用自底向上的方式利用过程maxHeapify把一个大小为elements.length的数组转换为最大堆。子数组elements(n/2 + 1..n)中的元素都是树的叶节点。

  　void buildMaxHeap(int[] elements) {
        for (int i = elements.length / 2; i >= 1; i--) {
           maxHeapify(elements, i);
        }
    }

堆排序：

    void heapSort(int[] elements) {
        for (int i = elements.length; i >= 2; i--) {
            int temp = elements[1];
            elements[1] = elements[i];
            elements[i] = temp;
            maxHeapify(elements, 1);
        }
    }