字符串哈希 矩阵哈希

题目

Matrix（https://ac.nowcoder.com/acm/problem/51003）

题目描述

给定一个M行N列的01矩阵（只包含数字0或1的矩阵），再执行Q次询问，每次询问给出一个A行B列的01矩阵，求该矩阵是否在原矩阵中出现过。

输入描述:

第一行四个整数M,N,A,B。
接下来一个M行N列的01矩阵，数字之间没有空格。
接下来一个整数Q。
接下来Q个A行B列的01矩阵，数字之间没有空格。

输出描述:

对于每个询问，输出1表示出现过，0表示没有。

示例1

输入
3 3 2 2
111
000
111
3
11
00
11
11
00
11
输出
1
0
1

备注:

对于40%的数据，A = 1。
对于80%的数据，A≤10。
对于100%的数据，A≤100，M,N≤1000，Q≤1000。

思路：

我们对这个矩阵哈希一下就可以了。然后用二维前缀和。

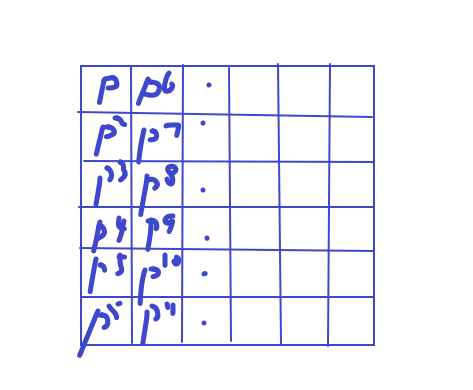
每个位置乘一个位权。p为进制。
我们要得到一个子矩阵时。

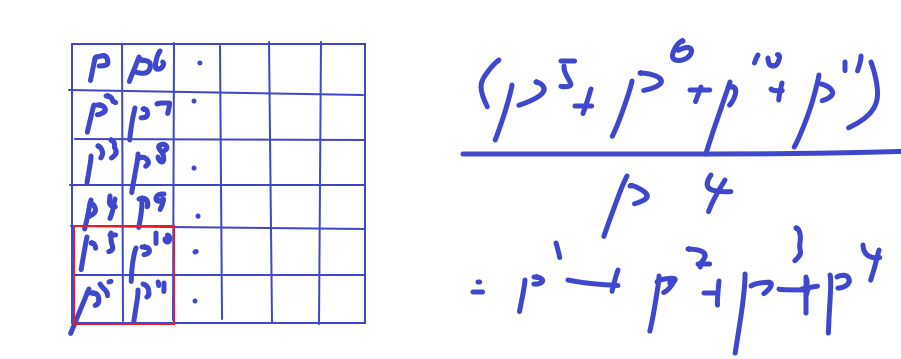
用二维前缀和/一个位权。

#include <bits/stdc++.h>
#define LL long long
using namespace std;

const int maxn=1000005;
LL a[1005][1005], b[1005][1005];

const LL mod=998244353, base=131;
LL p[1005], g[1005][1005];
LL is[1000005], tot=0;
void getp(){
    p[0]=1;
    for(int i=1; i<maxn; i++) p[i]=p[i-1]*base%mod;
}

LL getsum(int i, int j, int x, int y){
    return (a[x][y]-a[i-1][y]-a[x][j-1]+a[i-1][j-1]+2*mod)%mod;
}

LL ksm(LL a, LL b){
    LL ans=1;
    while(b){
        if(b&1){
            ans=a*ans%mod;
        }
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}

int main() {
    int n, m, A, B; scanf("%d%d%d%d", &n, &m, &A, &B);
    getp();
    for(int i=1; i<=n; i++){
        for(int j=1; j<=m; j++){
            scanf("%1lld", &a[i][j]);
            a[i][j]=a[i][j]*p[(i-1)*m+j]%mod;
        }
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++){
            a[i][j]+=(a[i-1][j]+a[i][j-1]-a[i-1][j-1]+mod);
            a[i][j]%=mod;
        }
    }
    for(int i=A; i<=n; i++){
        for(int j=B; j<=m; j++){
            LL ans=getsum(i-A+1, j-B+1, i, j)*ksm(p[(i-A)*m+j-B], mod-2)%mod;
            is[++tot]=ans;//把所有的A*B的矩阵哈希保存起来
        }
    }

    sort(is+1, is+tot+1);
    int q; scanf("%d", &q);
    while(q--){
        LL res=0;
        for(int i=1; i<=A; i++){
            for(int j=1; j<=B; j++){
                scanf("%1lld", &b[i][j]);
                b[i][j]=b[i][j]*p[(i-1)*m+j]%mod;
                res+=b[i][j]; res%=mod;
            }
        }
        int pos=lower_bound(is+1, is+tot+1, res)-is;

        if(is[pos]==res){
            printf("1\n");
        }
        else{
            printf("0\n");
        }
    }


    return 0;
}