ACM 悬线法总结
一般分为两种做法:
DP法 复杂度O(n*m)
问题引入
- 有一个n*m的矩阵,初始为白色,里面有s个黑色格子,现在问能在矩阵里面找到的最大不包含
黑色格子的子矩阵/正方形(n, m<=1000, s<=n*m)
例题:P2701 [USACO5.3]巨大的牛棚Big Barn(https://www.luogu.com.cn/problem/P2701)
题目描述
农夫约翰想要在他的正方形农场上建造一座正方形大牛棚。他讨厌在他的农场中砍树,想找一个能
够让他在空旷无树的地方修建牛棚的地方。我们假定,他的农场划分成 N x N 的方格。输入数据
中包括有树的方格的列表。你的任务是计算并输出,在他的农场中,不需要砍树却能够修建的最大
正方形牛棚。牛棚的边必须和水平轴或者垂直轴平行。
EXAMPLE
考虑下面的方格,它表示农夫约翰的农场,‘.'表示没有树的方格,‘#'表示有树的方格
1 2 3 4 5 6 7 8
1 . . . . . . . .
2 . # . . . # . .
3 . . . . . . . .
4 . . . . . . . .
5 . . . . . . . .
6 . . # . . . . .
7 . . . . . . . .
8 . . . . . . . .
最大的牛棚是 5 x 5 的,可以建造在方格右下角的两个位置其中一个。
输入格式
Line 1: 两个整数: N (1 <= N <= 1000),农场的大小,和 T (1 <= T <= 10,000)有树的方格的数量
Lines 2..T+1: 两个整数(1 <= 整数 <= N), 有树格子的横纵坐标
输出格式
只由一行组成,约翰的牛棚的最大边长。
输入
8 3
2 2
2 6
6 3
输出
5
思路
我们预处理
\(L[i][j]:(i, j)往左连续的最远'F'的位置\)
\(r[i][j]:(i, j)往右连续的最远'F'的位置\)
\(up[i][j]:(i, j)往上最大的高度\)
遍历矩阵然后在每个点DP一下就可以了。
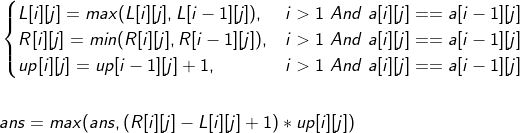
代码:
#include<bits/stdc++.h>
#define LL long long
using namespace std;
int s[1005][1005];
int l[1005][1005], r[1005][1005], up[1005][1005];
int main(){
int n, m, T; scanf("%d%d", &n, &T); m=n;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
s[i][j]=0;
l[i][j]=r[i][j]=j;
up[i][j]=1;
}
}
while(T--){
int x, y; scanf("%d%d", &x, &y);
s[x][y]=1;
}
for(int i=1; i<=n; i++){//预处理l[][]
for(int j=2; j<=m; j++){
if(s[i][j]==0&&s[i][j-1]==0){
l[i][j]=l[i][j-1];
}
}
}
for(int i=1; i<=n; i++){//预处理r[][]
for(int j=m-1; j>=1; j--){
if(s[i][j]==0&&s[i][j+1]==0){
r[i][j]=r[i][j+1];
}
}
}
int ans=0;
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
if(i>1&&s[i][j]==0&&s[i-1][j]==0){//DP
l[i][j]=max(l[i][j], l[i-1][j]);
r[i][j]=min(r[i][j], r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
int s=min((r[i][j]-l[i][j]+1), up[i][j]);
ans=max(ans, s);
}
}
printf("%d\n", ans);
return 0;
}
扩展法 复杂度O(s^2)
问题引入
- 有一个n*m的矩阵,初始为白色,里面有s个黑色格子,现在问能在矩阵里面找到的最大不包含
黑色格子的子矩阵/正方形(n, m<=5000, s<=1000)
题目描述
由于John建造了牛场围栏,激起了奶牛的愤怒,奶牛的产奶量急剧减少。为了讨好奶牛,John决定在牛场中建造一个大型浴场。
但是John的奶牛有一个奇怪的习惯,每头奶牛都必须在牛场中的一个固定的位置产奶,而奶牛显然不能在浴场中产奶,
于是,John希望所建造的浴场不覆盖这些产奶点。这回,他又要求助于Clevow了。你还能帮助Clevow吗?
John的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内,并且浴场的轮廓要与牛场的轮廓平行或者重合。
浴场不能覆盖任何产奶点,但是产奶点可以位于浴场的轮廓上。
Clevow当然希望浴场的面积尽可能大了,所以你的任务就是帮她计算浴场的最大面积。
输入格式
输入文件的第一行包含两个整数L和W,分别表示牛场的长和宽。文件的第二行包含一个整数n,表示产奶点的数量。
以下n行每行包含两个整数x和y,表示一个产奶点的坐标。所有产奶点都位于牛场内,即:0<=x<=L,0<=y<=W。
输出格式
输出文件仅一行,包含一个整数S,表示浴场的最大面积。
输入
10 10
4
1 1
9 1
1 9
9 9
输出
80
说明/提示
0<=n<=5000
1<=L,W<=30000
思路
来自王知昆大佬的论文:


代码
#include<bits/stdc++.h>
#define LL long long
using namespace std;
struct node {
LL x, y;
} a[5010];
int main() {
LL L, W;
scanf("%lld%lld", &L, &W);
int n;
scanf("%d", &n);
for(int i=1; i<=n; i++) {
scanf("%lld%lld", &a[i].x, &a[i].y);
}
a[++n]= {0, 0};
a[++n]= {0, W};
a[++n]= {L, 0};
a[++n]= {L, W};
sort(a+1, a+n+1, [](const node &a,const node &b) {
return (a.x==b.x)?a.y<b.y:a.x<b.x;
});
LL ans=0;
for(int i=1; i<=n; i++) {
LL l=0, h=W, v=L-a[i].x;
for(int j=i+1; j<=n; j++) {
if(a[j].y<=h&&a[j].y>=l||a[j].x==L) {//到边界
if(v*(h-l)<=ans) { //剪枝
break;
}
ans=max(ans, (h-l)*(a[j].x-a[i].x));
if(a[j].y==a[i].y) {
break;
}
if(a[j].y>a[i].y) {
h=min(h, a[j].y);
} else {
l=max(l, a[j].y);
}
}
}
l=0, h=W, v=a[i].x;
for(int j=i-1; j>=1; j--) {
if(a[j].y<=h&&a[j].y>=l||a[j].x==0) {//到边界
if(v*(h-l)<=ans) { //剪枝
break;
}
ans=max(ans, (h-l)*(a[i].x-a[j].x));
if(a[j].y==a[i].y) {
break;
}
if(a[j].y>a[i].y) {
h=min(h, a[j].y);
} else {
l=max(l, a[j].y);
}
}
}
}
sort(a+1, a+1+n, [](node &a, node &b) {
return a.y<b.y;
});
for(int i=1; i<n; i++) {
ans=max(ans, (a[i+1].y-a[i].y)*L);
}
printf("%lld\n", ans);
return 0;
}
总结
n*m 比较小用DP法
s^2 比较小用扩展法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号