[译]Cosine similarity
Cosine similarity [1][2] is a measure of similarity between two vectors of n dimensions by finding the cosine of the angle between them, often used to compare documents in text mining. Given two vectors of attributes, A and B, the cosine similarity, θ, is represented using a dot product and magnitude as
余弦相似度是利用两个n维向量的夹角余弦值来计算它们相似度的方法,经常用于在文本挖掘中比较文档.给定两个向量的属性(维度)A和B,它们的夹角θ,余弦相似度以点积和向量长度表示为
For text matching, the attribute vectors A and B are usually the term frequency vectors of the documents. The cosine similarity can be seen as a method of normalizing document length during comparison.
在文本匹配中,属性(维度)向量通常是文档的词频向量.余弦相似度可以看作一个在比较中规范化文档长度的方法.
The resulting similarity ranges from −1 meaning exactly opposite, to 1 meaning exactly the same, with 0 indicating independence, and in-between values indicating intermediate similarity or dissimilarity.
相似度的结果的范围从-1(表示完全相反)到1(表示完全相同),0表示互相独立,其余的值表示文档的相似度和相反度.
In the case of information retrieval, the cosine similarity of two documents will range from 0 to 1, since the term frequencies (tf-idf weights) cannot be negative. The angle between two term frequency vectors cannot be greater than 90°.
在信息检索的领域,余弦相似度的值的范围是从0到1,因为词频(tf-idf权重)不可能为负数.两个词频向量的夹角不可能大于90度.
This cosine similarity metric may be extended such that it yields the Jaccard coefficient in the case of binary attributes. This is the Tanimoto coefficient, T(A, B), represented as
余弦相似度的公式在二进制的情况下可以扩展到以Jaccard系数作为除数的值(分母).这是Tanimoto系数(广义Jaccard系数),T(A, B),表示为


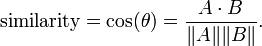


 浙公网安备 33010602011771号
浙公网安备 33010602011771号