LeetCode 1-10

ez:1、7、9 medium:2、3、5、6、8 hard: 4/10

1.两数之和（哈希表）

  vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int>m;
        for(int i=0;i<nums.size();i++)
        {
            int r=target-nums[i];
            if(m.count(r))return {m[r],i};
            m[nums[i]]=i;//存下标
        }
        return {};//
    }

2.两数相加（链表、竖式计算）

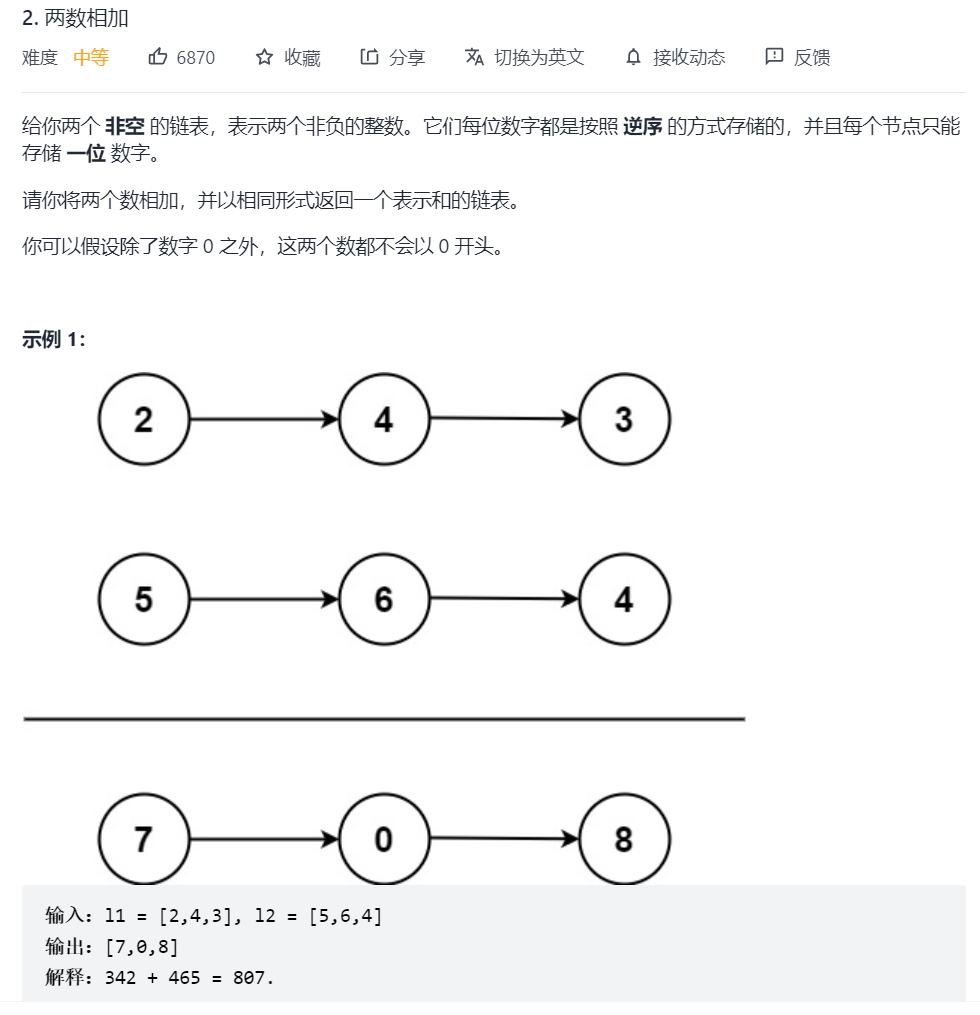
学到的知识点：
ListNode* 表示以该点开始的链表
往往构造虚拟节点来做 (开一个新链表)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        auto dummy=new ListNode(-1),cur=dummy;
        int t=0;
        while(l1||l2||t)
        {
            if(l1)t+=l1->val,l1=l1->next;
             if(l2)t+=l2->val,l2=l2->next;
             cur->next=new ListNode(t%10);
             cur=cur->next;
             t/=10;
        }
        return dummy->next;

    }
};

3. 无重复字符的最长子串（双指针）

思路:双指针 如果s[i]重复了 移动j直到s[i]字符只剩下第i个位置上的那一个

 int lengthOfLongestSubstring(string s) {
        unordered_map<int,int>m;
        int res=0;
        for(int i=0,j=0;i<s.size();i++)
        {  
            m[s[i]]++;
            while(m[s[i]]>1)m[s[j]]--,j++;
            res=max(res,i-j+1);
        }
        return res;

    }

4. 寻找两个正序数组的中位数（归并排序 暂时只会这种解法O(n+m)）

  double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
       double a[2010];
        int i=0,j=0,k=0;
        while(i<nums1.size()&&j<nums2.size())
        {
            if(nums1[i]<nums2[j])a[k++]=nums1[i++];
            else a[k++]=nums2[j++];
        }
        while(i<nums1.size())a[k++]=nums1[i++];
        while(j<nums2.size())a[k++]=nums2[j++];
       if(k&1)return a[k/2];
       else return (a[k/2]+a[k/2-1])/2;
    }

5. 最长回文子串 (枚举)

思路：固定回文串最中间的字符从它向两边枚举
回文串的形式肯定是二者其一
长度为奇数 从中间字符往两侧枚举
长度为偶数 中间两个字符相同 从它们往两边枚举

 string longestPalindrome(string s) {
        
        int n=s.size();
        string res;
        
        for(int i=0;i<n;i++)
        {
            int l=i-1,r=i+1;
            while(r<n&&l>=0&&s[l]==s[r])r++,l--;
//这样的话找到的回文串长度为(r-1)-(l+1)+1
            if(r-l-1>res.size())res=s.substr(l+1,(r-1)-(l+1)+1);
            l=i,r=i+1;
            while(r<n&&l>=0&&s[l]==s[r])r++,l--;
            if(r-l-1>res.size())res=s.substr(l+1,(r-1)-(l+1)+1);
        }
        return res;
    }

6.Z字型变换（找规律）

教训：这道题我觉得棘手，与其盯着屏幕空想 更好的选择是用笔在纸上找规律
规律就是 ：
1.每隔2numRows-2有一个
2.除了第一行和最后一行 k+2numRows-2-2j也会有一个
3.判断下边界 小于s.size()

string convert(string s, int numRows) {
        if(numRows==1)return s;
        int n=s.size();string ans;

            for(int j=0;j<numRows;j++)
            {
               
                if(j==0||j==numRows-1)
                {
                    if(j<n) ans+=s[j];
                    int k=j;
                    while(k+2*numRows-2<n)
                    {
                        ans+=s[k+2*numRows-2];
                        k+=2*numRows-2;
                    }
                }
                else
                {
                    if(j<n)ans+=s[j];
                    int k=j;
                    while(k+2*numRows-2<n)
                    {
                         ans+=s[k+2*numRows-2-2*j];
                        ans+=s[k+2*numRows-2];
                        k+=2*numRows-2;
                    }
                    if(k+2*numRows-2>=n&&k+2*numRows-2-2*j<n)ans+=s[k+2*numRows-2-2*j];
                }
            }
        return ans;

    }

7. 整数反转

这题得想办法判断越界 可以将本来乘法转换成除法
10ans+x%10>INT_MAX ?? //ans10为之前反转对应的数

    int reverse(int x) {
        int ans=0;
        while(x)
        {
            if(x>0&&ans>(INT_MAX-x%10)/10)return 0;
            if(x<0&&ans<(INT_MIN-x%10)/10)return 0;
            ans=ans*10+x%10;
            x/=10;
        } 
        return ans;
    }

8. 字符串转换整数 (atoi) (模拟)

int myAtoi(string s) {
        int i=0;
        while(s[i]==' ')i++;
        if(s[i]=='-'||s[i]=='+')
        {
            bool flag=false;
            if(s[i]=='-')flag=true;
            i++;
            long long res=0;
            while(s[i]>='0'&&s[i]<='9')
            {
                res*=10;
                if(flag)res-=(s[i]-'0');
                else res+=(s[i]-'0');
                if(res>INT_MAX)return INT_MAX;
                if(res<INT_MIN)return INT_MIN;
                i++;
            }
            return res;

        }
        else if(s[i]>='0'&&s[i]<='9')
        {
              long long res=0;
            while(s[i]>='0'&&s[i]<='9')
            {
                res*=10;
                res+=(s[i]-'0');
                if(res>INT_MAX)return INT_MAX;
                if(res<INT_MIN)return INT_MIN;
                 i++;
            }
            return res;
           
        }
        return 0;

    }

9. 回文数(字符串 暂时只想到最直接的解法)

 bool isPalindrome(int x) {
        if(x<0)return false;
        string s;
        while(x)
        {
            s+=x%10+'0';
            x/=10;
        }
      for(int i=0;i<s.size();i++)
      {
          if(s[i]!=s[s.size()-1-i])return false;
      }
      return true;
    }

10.正则表达式匹配（DP）

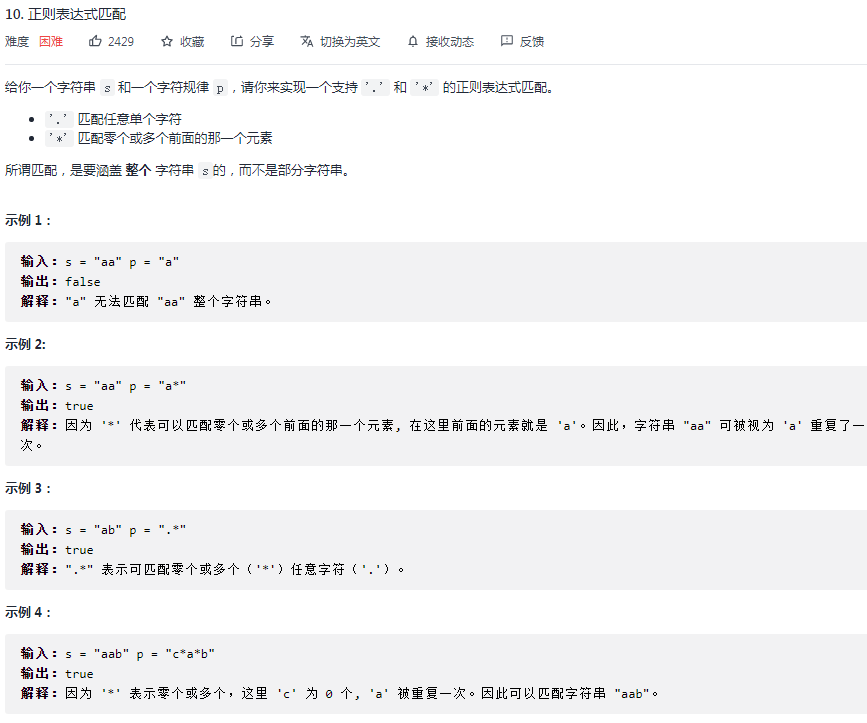
感想：乍一眼棘手，实际也棘手。动态规划题吃经验 状态表示是经验看出来的学出来的 不是凭空想出来的 对于我来说

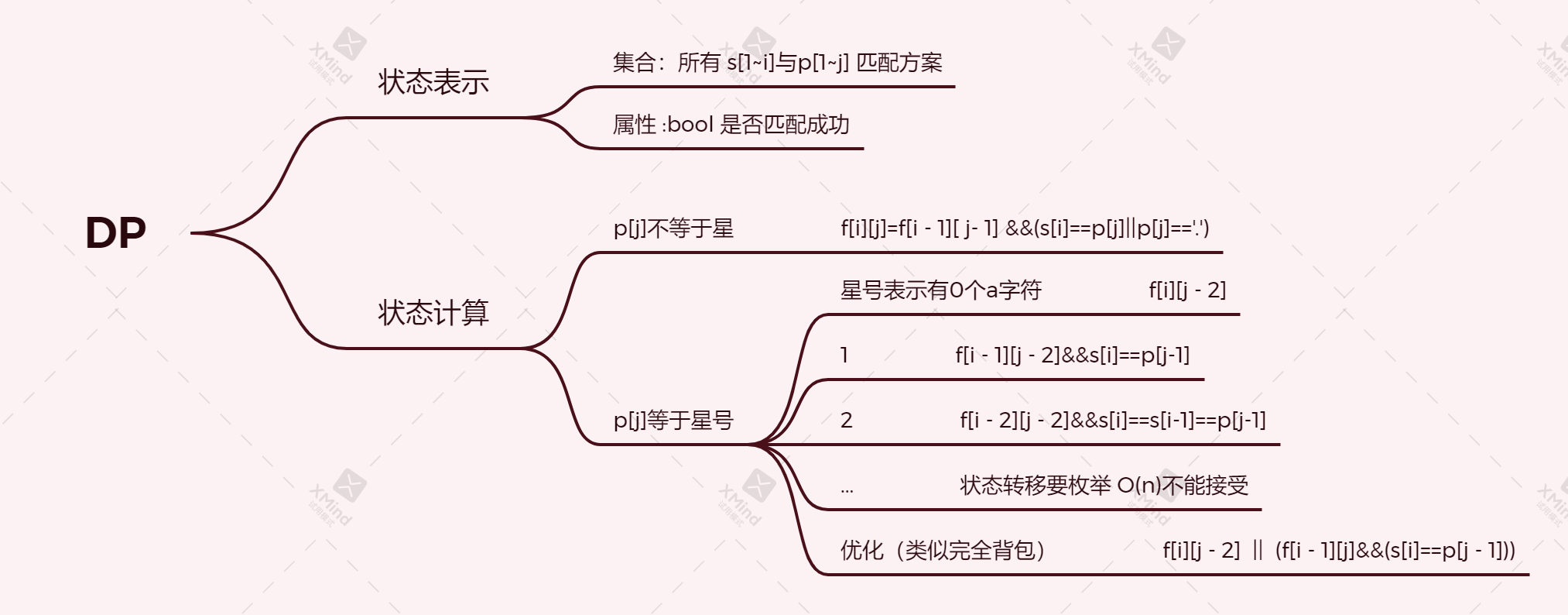
优化 f[i][j]  = f[i][j-2] || f[i-1][j-2]&&s[i]==p[j-1] || f[i-2][j-2]&&s[i]==s[i-1]==p[j-1] ... 
     f[i-1][j]=              f[i-1][j-2]               || f[i-2][j-2]&&s[i]==p[j-1]  ... ...
所以f[i][j]=f[i][j-2]||  f[i-1][j] &&(p[j-1]==s[i])

从感性上认识呢 比如 a*能匹配 " " "a" "aa" 这三个
因为 " "第一次匹配成功 所以再加上一个a也能成功 "a"成功了 "aa"也自然顺理成章。
也就是如果s[1~i-1]，p[j]成功了只需要判断再一次加的字符是否是a即可。

 bool isMatch(string s, string p) {
        int n=s.size(),m=p.size();
        s=' '+s,p=' '+p;//习惯 下标从一开始
        vector <vector<bool>> f(n+1,vector<bool>(m+1));//二维数组
        f[0][0]=true;
        for(int i=0;i<=n;i++)//从0开始 因为a*能匹配" " 
        {
            for(int j=1;j<=m;j++)
            {
                if(j+1<=m&&p[j+1]=='*')continue;// a*当成整体一起做
                if(p[j]!='*'){
                    if(i)f[i][j]=f[i-1][j-1]&&(s[i]==p[j]||p[j]=='.');
                }
                else{//状态转移 枚举on变成了o1
                   f[i][j]=f[i][j-2]||  i&&f[i-1][j] &&(p[j-1]==s[i]||p[j-1]=='.');
                }
            }
        }
        return f[n][m];
    }