三次样条插值(Cubic Spline Interpolation)
样条插值是一种工业设计中常用的、得到平滑曲线的一种插值方法,三次样条又是其中用的较为广泛的一种。本篇介绍力求用容易理解的方式,介绍一下三次样条插值的原理,并附C语言的实现代码。
1. 三次样条曲线原理
假设有以下节点
1.1 定义
样条曲线![]() 是一个分段定义的公式。给定n+1个数据点,共有n个区间,三次样条方程满足以下条件:
是一个分段定义的公式。给定n+1个数据点,共有n个区间,三次样条方程满足以下条件:
a. 在每个分段区间![]() (i = 0, 1, …, n-1,x递增),
(i = 0, 1, …, n-1,x递增), ![]() 都是一个三次多项式。
都是一个三次多项式。
c. ![]() ,导数
,导数![]() ,二阶导数
,二阶导数![]() 在[a, b]区间都是连续的,即
在[a, b]区间都是连续的,即![]() 曲线是光滑的。
曲线是光滑的。
所以n个三次多项式分段可以写作:
其中ai, bi, ci, di代表4n个未知系数。
1.2 求解
已知:
a. n+1个数据点[xi, yi], i = 0, 1, …, n
b. 每一分段都是三次多项式函数曲线
c. 节点达到二阶连续
d. 左右两端点处特性(自然边界,固定边界,非节点边界)
根据定点,求出每段样条曲线方程中的系数,即可得到每段曲线的具体表达式。
插值和连续性:
微分连续性:
样条曲线的微分式:
将步长![]() 带入样条曲线的条件:
带入样条曲线的条件:
c. 将bi, ci, di带入![]() (i = 0, 1, …, n-2)可得:
(i = 0, 1, …, n-2)可得:
端点条件
由i的取值范围可知,共有n-1个公式, 但却有n+1个未知量m 。要想求解该方程组,还需另外两个式子。所以需要对两端点x0和xn的微分加些限制。 选择不是唯一的,3种比较常用的限制如下。
a. 自由边界(Natural)
则要求解的方程组可写为:
b. 固定边界(Clamped)
首尾两端点的微分值是被指定的,这里分别定为A和B。则可以推出
将上述两个公式带入方程组,新的方程组左侧为
c. 非节点边界(Not-A-Knot)
指定样条曲线的三次微分匹配,即
新的方程组系数矩阵可写为:
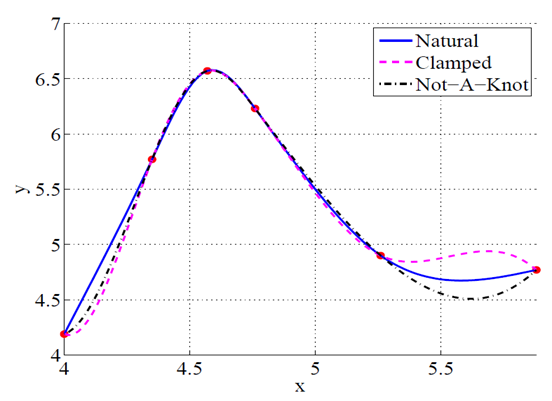
右下图可以看出不同的端点边界对样条曲线的影响:
1.3 算法总结
假定有n+1个数据节点
b. 将数据节点和指定的首位端点条件带入矩阵方程
c. 解矩阵方程,求得二次微分值![]() 。该矩阵为三对角矩阵,具体求法参见我的上篇文章:三对角矩阵的求解。
。该矩阵为三对角矩阵,具体求法参见我的上篇文章:三对角矩阵的求解。
d. 计算样条曲线的系数:
其中i = 0, 1, …, n-1
2. 例子
以y=sin(x)为例, x步长为1,x取值范围是[0,10]。对它使用三次样条插值,插值前后对比如下:





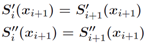
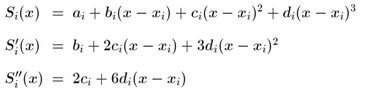
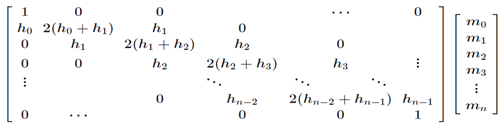
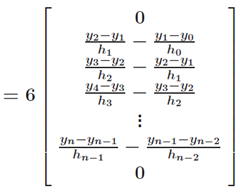
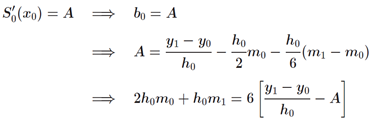
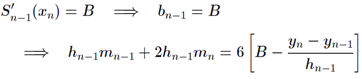
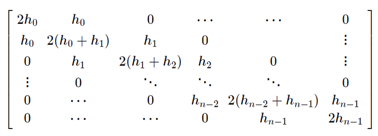
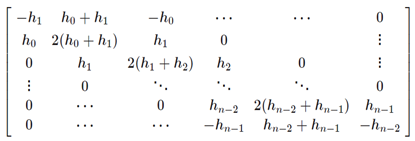
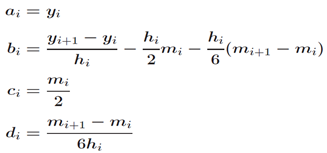

 浙公网安备 33010602011771号
浙公网安备 33010602011771号