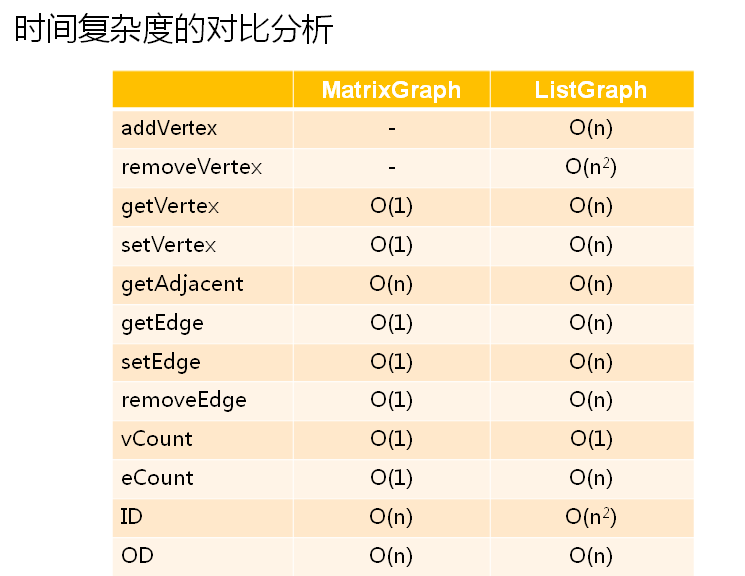
第74课 图的遍历（广度优先遍历BFS）

 

 

 

 

 

 

 

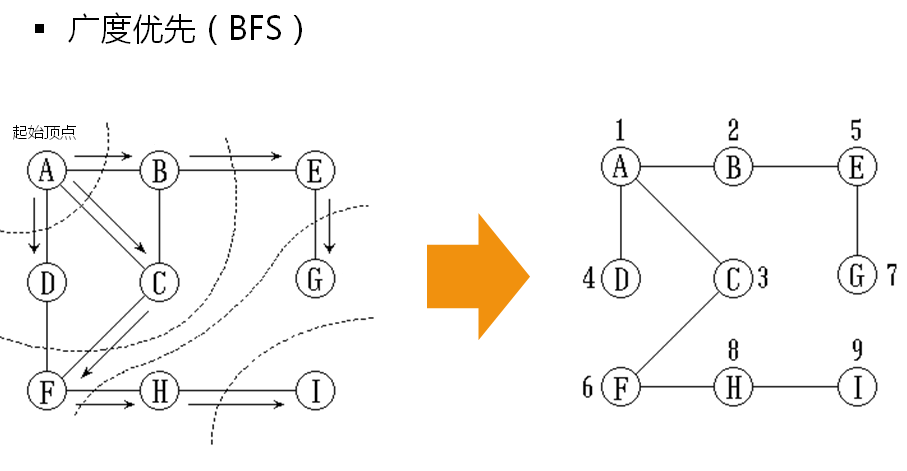
广度优先相当于对顶点进行分层，层次遍历。

 

 

 以i为顶点对图进行广度优先遍历

（1）三个原材料准备queue （保存图的顶点） return  （保存弹出的顶点）两个队列和一个visited数组（标记对应顶点是否访问过）

（2）visited=0 标记初始状态每个顶点都没有访问

（3）起始顶点压入queue队列

（4）循环 queue队列  -----  判断队列内是否还有顶点

（5）取出v顶点的对头元素  v=queue.front(); queeu.remove();

（6）判断取出的对头元素v有没有访问过

（7）没有访问----取v顶点的邻接顶点，压入queue队列

（8）v顶点访问过了，加入return队列（ret），且标记visited[v]=true被访问

（9）头元素v访问过了，扔掉接着算法遍历

　　　　　　　　　　 广度优先遍历的结果是数组

 

 

 

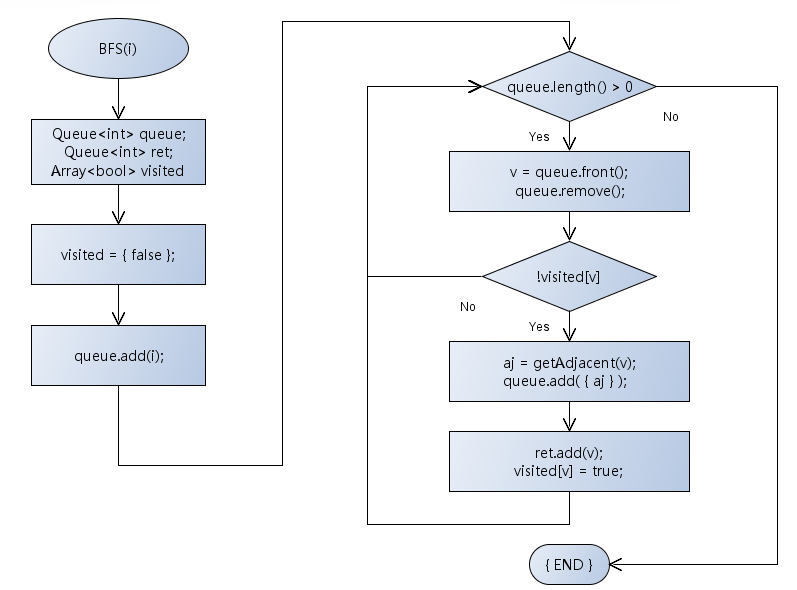
 在Graph.h中添加BFS函数：

 

 

测试程序如下：

 1 #include <iostream>
 2 #include "BTreeNode.h"
 3 #include "ListGraph.h"
 4 #include "MatrixGraph.h"
 5 
 6 using namespace std;
 7 using namespace DTLib;
 8 
 9 
10 int main()
11 {
12     MatrixGraph<9, char, int> g;  //实例无向图 权值未指定
13     const char* VD = "ABEDCGFHI";
14 
15     for(int i=0; i<9; i++)
16     {
17         g.setVertex(0, VD[i]);  //设置与顶点相关联的数据元素值：北京上海  这里是ABCDEFGH
18     }
19 
20     g.setEdge(0, 1, 0);  //无权值  0 代替    无向图可用有向图表示 ----> 对称的设置边
21     g.setEdge(1, 0, 0);
22 
23     g.setEdge(0, 3, 0);
24     g.setEdge(3, 0, 0);
25 
26     g.setEdge(0, 4, 0);
27     g.setEdge(4, 0, 0);
28 
29     g.setEdge(1, 2, 0);
30     g.setEdge(2, 1, 0);
31 
32     g.setEdge(1, 4, 0);
33     g.setEdge(4, 1, 0);
34 
35     g.setEdge(2, 5, 0);
36     g.setEdge(5, 2, 0);
37 
38     g.setEdge(3, 6, 0);
39     g.setEdge(6, 3, 0);
40 
41     g.setEdge(4, 6, 0);
42     g.setEdge(6, 4, 0);
43 
44     g.setEdge(6, 7, 0);
45     g.setEdge(7, 6, 0);
46 
47     g.setEdge(7, 8, 0);
48     g.setEdge(8, 7, 0);
49 
50     SharedPointer< Array<int> > sa = g.BFS(0);   //广度优先遍历   起始顶点是 0 号节点
51 
52     for(int i=0; i<sa->length(); i++)
53     {
54         cout << (*sa)[i] << " ";  //打印结果
55     }
56 
57     cout << endl;
58 
59     return 0;
60 }

 广度优先的本质就是层次遍历。

结果如下：

 

 

小结：