菜鸟谈谈二分图的最佳匹配
参考《啊哈算法》
有一种很特别的图,就做二分图,那什么是二分图呢?就是能分成两组,S,T。其中,S上的点不能相互连通,只能连去T中的点,同理,T中的点不能相互连通,只能连去S中的点。这样,就叫做二分图。
举个很通俗的例子,现在有三个男生和三个女生,要组队一起去报名旅游(情侣报名可以半价哦!),所以,他们就想尽办法凑成一对,就算不是情侣,都说是啦,为了减钱,更可况,我们这些单身狗就是靠这些机会脱单的, ̄□ ̄||。……..为什么可以看成二分图呢?你想啊,男和男在一对,搞基啊?所以,同性的我们规定不能在一起。那么现在问题来了,我现在想知道它们6个人,能组成多少对?这就引入了一个新的问题:二分图的最【大】匹配。顾名思义,就是求二分图中能组成的最大匹配数,比如那6个最多能组成3对,但是能不能组成还是要看条件的。因为小时候爷爷教过我们,不能随便和陌生人打交道嘛,所以我们这里规定,它们只有在认识(就是图能连通) 的情况下,才能组成一对。
现在有男孩:A、B、C
女孩:X、Y、Z
下面给出他们的关系,看清楚那。A认识X、Y
B认识Y、Z 由于C比较内向,只认识X
好啦,现在就要求他们最多能组成多少对啦!唉,为了减钱,费点脑力,值!其实一看就知道了:3对。A—Y B—Z C—X 。但是,我们没办法一下子就得出这个结论的,为什么呢?因为A B C本来互不认识,A也不知道C是不是认识X,所以,A去搭配X或者Y对于A来说是一样的,为什么一定要A搭配Y?所以,我们就算他们不认识,我们也要用算法解他们出来,这就是我们的二分图的最大匹配。现在我们来模拟一下整个过程?首先,A来到X小姐面前,礼貌地问:Could I travel with you? X小姐想都没想,立马答应了(这里我们假设女的一定要答应任何一个男的,为什么?无解,因为我们只是求他们搭配的最大对数,其他的都是次要的,但是我们后面说的最佳匹配,那就不同了)。然后到B先生了,首先,他来到Y中,和Y组合了一起。现在轮到C先生了,C只认识X,然后他去到X小姐身边,说:I wanner ……遗憾的是:X小姐说:我已经和别人组成一队了啊?(怎么办?C先生颜值好像比较高,好想和他一起组队啊……)咦?“你等等,我去问问A先生能不能和别人一起组队先。”X小姐说。然后A先生就只能跑去Y小姐那里了(因为A先生也认识Y小姐),礼貌地问:Could I travel with you? 哇塞!Y小姐最喜欢会说英语的男人了,但是我已经有队伍了啊。咦?你们猜到了吧,如法炮制。对A说:你等等,我问问B能不能和别人组队。然后到B了,他去问Z,我们….能在一起….组队吗?没人搭理的Z小姐当然愿意啦,就说:“我正好空着呢!我们一起吧!”。然后,B就告诉Y,我找到别人啦,88。Y告诉A,我们可以一起去啦,yeah!!!(心想)。然后A告诉X,我找到人啦,886。然后X告诉C,我们可以一起去啦。 ̄□ ̄||…..弄了那么久,终于使匹配数增加一了,这里我们把它叫做增广路。增广路的作用就是“改进”匹配方案(也就是增加匹配对数),那么我们怎么确定他就是最大匹配呢?如果当前匹配方案下再也找不到增广路,那就是最大匹配了,算法如下:

#include <stdio.h> #include <stdlib.h> #include <string.h> int n,m;//顶点数n和边的数目m int e[51][51];//保存一个无向图 int book[51];//每次都标记那个去了和那个没去 int match[51];//标记那个是匹配那个的 #define inf 9999//假设的无穷大 int dfs (int u) { int i; for (i=1;i<=n;i++) { if (book[i]==0&&e[u][i]==1)//这个点在同一次上没去过,而且他们能联通 { book[i]=1;//这个点已经尝试过了 if (match[i]==0||dfs(match[i]))//这个点还没有被匹配, //或者,他可以匹配其他的人 { //他们就能够匹配 match[i]=u;//判断哪个,就是修改那个 //match[u]=i;不用的,错误的 return 1; } } } return 0; } void work () { scanf ("%d%d",&n,&m);//输入顶点数n和边的数目m int i; int j; for (i=1;i<=n;i++) { for (j=1;j<=n;j++) { if (i==j) e[i][j]=0;//初始化 else e[i][j]=inf; } } for (i=1;i<=m;i++) { int u,v; scanf ("%d%d",&u,&v); e[u][v]=1; e[v][u]=1;//无向图 } int i_count=0; for (i=1;i<=n;i++)//尝试遍历每一个顶点 { memset (book,0,sizeof(book)); if (dfs(i)) { i_count++;//若能找到新的匹配,就++ } } printf ("%d\n",i_count); return ; } int main () { work (); system ("pause"); return 0; }
远处传来一阵呼声:“此路是我开,此树是我栽,要想过此路,留低买路财!!!”————他们遇到山贼了!怎么办怎么办?对面虽然只有三个山贼,但是实力估计去到14点,我们虽说有六个人,但是,A搭配Y,力量有7点,B搭配Z,力量只有1点,(怎么那么少?嘿嘿,他们两个都是文化生,不好动武嘛!),C搭配X,力量有5点, ̄□ ̄|| 还差一点,难道这次旅游就倒在这里?是给钱还是怎样呢?想来想去,A和C就说,B你为什么那么弱?只有1点?
B:………… 要是能高一点,也就好了,这样吧,我们重新搭配吧,因为经过昨晚的狂欢,他们已经是互相认识了,另外,他们的搭配默契度有所不同哦,(默契度就是他们的力量),现在看看这个表格:
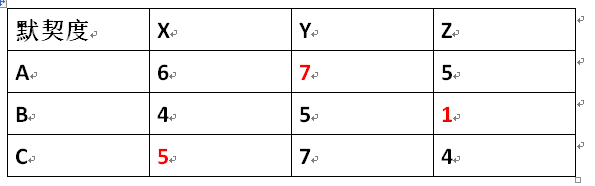
看来他们的默契度也不是很少,只是,B搭配Z太小了,这是她们打不过山贼的短板!现在我们要怎样重组,才能打赢山贼呢?这就是我们的:二分图的最【佳】匹配啦!顾名思义,就是在考虑能搭配的情况下,又要使得搭配后,整张图边的权值加起来是最大的,这样的匹配,我们称为最佳匹配。也叫KM算法
贪心选边:何为贪心选边?贪心,就是一个寻找局部最优解的过程,至于是不是全局最优解,需要证明才能用。就算不能每次选出最大值的边,但是选出来的边的总和都是前n个最优的。通俗点讲,就是每次都选择搭配最高的,就是现在的A,搭配Y是最高的,所以我们先把A—>Y。至于这样会不会影响后面的呢?就好像BàY也是B中最高的,是5。这样就会产生歧义,因为一个人不能同时匹配多个嘛。那么究竟是A-->Y,还是B-->Y呢?有人笑了,这不很简单吗?A-->Y是7,B-->Y是5,当然是A-->Y啊,比较大啊。那答案是不是这样的呢?其实很容易证明他是不一定的,因为我们这里求的是全局最优解,不能因为个人匹配最大而否定别人,可以举个极端的例子:假如:现在的B除了搭配Y是5外,他搭配X,Z都是比较小的,是-inf,就是负无穷,那么,当然要让让B啊,不然就不是全局最优解了。那么,我们怎么来确定谁选谁呢?
这里我们用两个数组,也称为标杆,fx[]和fy[]。
其中,开始的时候,fx[]的值为匹配的最大值,fy[]的值先初始化为0。
// fx[]={0,7,5,7},fy[]={0,0,0,0},
//前面一个fx[0]我没用,同理fy
这里我们判断两人是否能匹配的时候,多加一个条件,就是fx[u]+fy[i]==e[u][i];//就是这两个人匹配的值,要存在这个图中。开始的时候相加是最大值。
我们先来看看KM算法的实现:

void do_km() { int i,j; int d=inf; for (i=1;i<=n ;i++ ) { if (vx[i]==1) { for (j=1;j<=n ;j++ ) { if (vy[j]==0) { if (d>fx[i]+fy[j]-e[i][j]) { d=fx[i]+fy[j]-e[i][j]; //选出边差的最小值 } } } } } //对于每个存在vx中的 //和每个存在vy中的 for (i=1;i<=n ;i++ ) { if (vx[i]==1) { fx[i] -= d; vx[i]=0;//取消标记 } if (vy[i]==1) { fy[i] += d; vy[i]=0; } } //这样,由于vx比vy总是要多,所以,总体减小得 return ; }
有什么用呢?就是用来比较是不是应该这样匹配。此话怎讲?就是,开始的时候,A和Y搭配了,轮到B选人了,B说:我要和Y搭配,“为什么?“A说,B:…….对啊,为什么?大家都是最大值,凭什么我让你?这样,他们产生了隔阂,好吧,KM算法帮你们吧,KM:你们大家都觉得自己说最大的,但是你们能不能为全局想想,我要的是全局最大而不是你们自己最大。这样吧,A,你除了搭配Y外,搭配其他的,相对于搭配Y来说,你的力量值会减小多少?A:减少1,我和X搭配有6,KM:好好,那么,B一样,你除了搭配Y,的力量值减小多少?B:减少1,我和X搭配的话,力量有4。此时我们用d来记录他们的最小差值。现在d=1;此时:fx和fy做出了相应的变化。先讲规律再解释:那就是:所有vx[i]==1的i,fx[i] -= d;所有的vy[i]==1的i,fy[i] += d;就是所有主动去过搭配别人的,因为产生过歧义,所以大家都降低了自己的要求。而所有被人邀请过的,都摆起了架子。这样,由于,vx[]的数目总是比vy[]的数目多的。为什么?你想啊,你本来标记vy[i]=1;是有多困难啊,比标记vx[]难很多。这样,总体来说,fx[]和fy[]的和总体减少,这样,就为我们添加一条新的边提供了空间。此时,我们再一次为B找匹配,先来看看fx和fy的值
fx[]={6,4,7} fy[]={0,1,0},这样,B就能匹配去X了。KM:那么就是大家减少都一样, B你就先搭配X吧。B:OK,为全局考虑。
后面的处理,其实是一样的,到C了,如果认真的同学,一步一步运算的话,可以发现,C没得搭配,本来C是去搭配Y的,但是,fy[2]=1,他已经摆起了架子,所以,C这么大要求已经不能满足Y了,所以,C自己再进行一次KM算法,C减去了1(一步一步模拟,就知道为什么是减去1而不是减去2了),就能搭配Y啦,喂喂喂!好玩吗?Y是A的,你们干嘛了,同理,发现A去搭配X是6减小1,而C搭配X是5减小2,所以,A就搭配X啦,B:………X不是我的吗?同理,发现X搭配Z是1(此时X已经不能搭配Y了,因为在递归中,vy[2]已经被标记),减小3,A搭配Z是5减小1,这样,A就搭配了Z了,到此,算法结束,最优解产生,A搭配Z是5,B搭配X是4,C搭配Y是7。
最优解的ans=16,已经可以打败土匪了,累……去来旅游不容易啊,也看出了,生活处处是算法啊。
本人初出茅庐,如有任何错误,希望读者指出,本人感觉不尽。
posted on 2016-01-21 13:19 stupid_one 阅读(4134) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号