生成2D三角形均匀网格剖分矩阵代码（逐行注释版）

import matplotlib.pyplot as plt
import numpy as np
# 输入:一个矩形区域[left,right],[bottom,top]；x方向划分的网格数目N1，y方向划分的网格数目N2
# 输出：P矩阵（P矩阵的第k列存储第k个网格点的坐标）T矩阵（T矩阵的第n列存第n个网格单元的所有网格顶点的全局编号）
def generate_mesh_2D(left,right,bottom,top,N1,N2):
    # Nm 表示节点的总数
    Nm =  (N1+1)*(N2+1)
    # N 表示三角形单元的总数
    N = 2* N1 * N2
    # h1 表示x方向的步长
    h1 = (right-left)/N1
    # h2 表示y方向的步长
    h2 = (top - bottom)/N2
    # 初始化矩阵P 行数为2 因为要放置x，y坐标 列数为Nm 因为一共有Nm个节点
    P = np.zeros((2,Nm))
    for n in range(1,Nm+1):
        # 指标n表示目前需要填写矩阵P的第n列 也就是需要把第n个节点的坐标填入P矩阵的n-1 索引处
        # 为了计算第第n个点的坐标 需要得到第n个点在平面上的位置（也就是处在第几行第几列 n对N2取商和余数）
        # n 除N2的商shang反映了第n个点在哪一列 例如：n//N2 == 0 那么第n个点 就在第 0 列 n//N2 == 1 那么第n个点就在第1列 以此类推。。
        shang = n // (N2+1)
        # n 除 N2 的余数yushu反映了第n个点在哪一行 例如： n % N2 == 0 那么就在最上面那行 n % N2 == 1那么就在最下面那行 n%N2 == 2 就在从下至上数第2行
        yushu = n % (N2+1)
        # 根据几何关系，x坐标是left加上shang*h1
        x_cor = left + shang*h1
        # y坐标可以通过 n % N2 的余数根据几何关系得到
        if yushu == 0:
            y_cor = top
            x_cor = (shang-1)*h1 + left
        else:
            y_cor = bottom + (yushu-1)*h2
        # 第n个点的坐标应该存储在矩阵P索引为 n-1 的列 索引为0的行存横坐标x_cor 索引为1的行存纵坐标y_cor
        P[0][n-1] = x_cor 
        P[1][n-1] = y_cor
    # 初始化矩阵T 行数为3 因为要放置3个点的全局编号 列数为N 因为一共有N个单元
    T = np.zeros((3,N))
    # T矩阵的定义为：第k列 存储第k个单元所有顶点的全局编号 k = 1,...,N 
    for k in range(1,N+1):
        # 与P矩阵类似 需要计算yushu_T = k % (2*N2) shang_T = k// (2*N2) 再根据yushu_T shang_T 的几何关系计算得到第k个单元所有点的全局编号
        yushu_T = k % (2*N2)
        shang_T = k // (2*N2)
        if k == 2:
            print(yushu_T)
            print(shang_T)
        # 先判断 第k个三角形是哪种三角形（一共有两种三角形 一种是左下的三角形(记为type_tri = 1) 一种是右上的三角形（记为type_tri = 2））yushu_T % 2 == 0是右上的三角形 yushu_T % 2 == 1是左下的三角形
        if yushu_T % 2 == 0:
            type_tri = 2 
        else:
            type_tri = 1
        # 分两种情况进行讨论（右上的三角形type_tri == 2 和左下三角形 type_tri == 1） 
        #　后面就不注释了，其实画画图就明白了　就是最简单的几何位置和坐标的对应关系
        if type_tri == 2:
            if yushu_T == 0:
                local_index_1 = (shang_T)*(N2+1)
                local_index_2 = (shang_T+1)*(N2+1)-1
                local_index_3 = (shang_T+1)*(N2+1)
            else:
                local_index_1 = (N2+1)*shang_T + (yushu_T//2) + 1
                local_index_2 = (N2+1)*(shang_T+1) + (yushu_T//2)
                local_index_3 = (N2+1)*(shang_T+1) + (yushu_T//2) + 1
        else:
            local_index_1 = (N2+1)*shang_T + (yushu_T//2) + 1
            local_index_2 = (N2+1)*(shang_T+1) + (yushu_T//2) + 1
            local_index_3 = (N2+1)*shang_T + (yushu_T//2) + 2
        T[0][k-1] = local_index_1
        T[1][k-1] = local_index_2
        T[2][k-1] = local_index_3
    return P , T

测试用例 1 如下图所示的网格

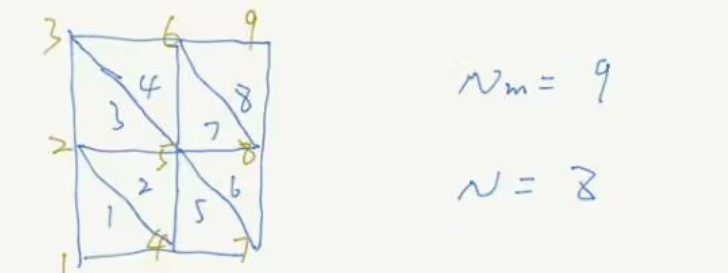
按下式进行传参

P,T = generate_mesh_2D(0,1,0,1,2,2)

程序输出结果为

P矩阵为：
[[0.  0.  0.  0.5 0.5 0.5 1.  1.  1. ]
 [0.  0.5 1.  0.  0.5 1.  0.  0.5 1. ]]
T矩阵为：
[[1. 2. 2. 3. 4. 5. 5. 6.]
 [4. 4. 5. 5. 7. 7. 8. 8.]
 [2. 5. 3. 6. 5. 8. 6. 9.]]

测试用例 2 如下图所示的网格

按下式进行传参

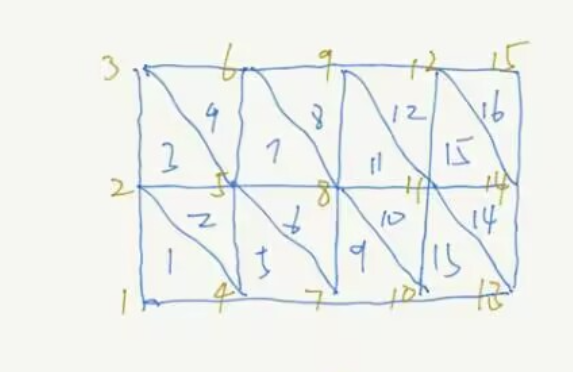
P,T = generate_mesh_2D(0,2,0,1,4,2)

程序输出结果为

P矩阵为：
[[0.  0.  0.  0.5 0.5 0.5 1.  1.  1.  1.5 1.5 1.5 2.  2.  2. ]
 [0.  0.5 1.  0.  0.5 1.  0.  0.5 1.  0.  0.5 1.  0.  0.5 1. ]]
T矩阵为：
[[ 1.  2.  2.  3.  4.  5.  5.  6.  7.  8.  8.  9. 10. 11. 11. 12.]
 [ 4.  4.  5.  5.  7.  7.  8.  8. 10. 10. 11. 11. 13. 13. 14. 14.]
 [ 2.  5.  3.  6.  5.  8.  6.  9.  8. 11.  9. 12. 11. 14. 12. 15.]]

测试用例 3 如下图所示的网格

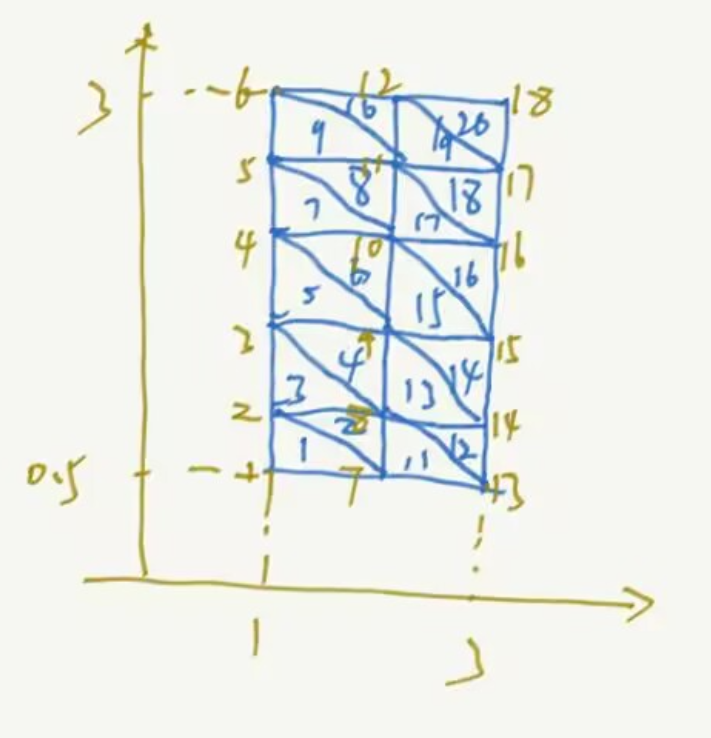
按下式进行传参

P,T = generate_mesh_2D(1,3,0.5,3,2,5)

程序输出结果为

P矩阵为：
[[1.  1.  1.  1.  1.  1.  2.  2.  2.  2.  2.  2.  3.  3.  3.  3.  3.  3. ]
 [0.5 1.  1.5 2.  2.5 3.  0.5 1.  1.5 2.  2.5 3.  0.5 1.  1.5 2.  2.5 3. ]]
T矩阵为：
[[ 1.  2.  2.  3.  3.  4.  4.  5.  5.  6.  7.  8.  8.  9.  9. 10. 10. 11.
  11. 12.]
 [ 7.  7.  8.  8.  9.  9. 10. 10. 11. 11. 13. 13. 14. 14. 15. 15. 16. 16.
  17. 17.]
 [ 2.  8.  3.  9.  4. 10.  5. 11.  6. 12.  8. 14.  9. 15. 10. 16. 11. 17.
  12. 18.]]

这三个测试用例表明，程序输出的矩阵P，T结果与实际网格信息P，T一致，这验证了我们生成P，T矩阵的函数generate_mesh_2D是正确的。

参考资料：bilibili上何晓明老师的有限元程序课
课程链接：https://www.bilibili.com/video/BV1e5411H7AP/?spm_id_from=333.1391.0.0&vd_source=3b7abf5a53a2fb64ebac8f562a88de45