Machine Learning 第一二周

ML week 1 2

---

一、关于machine learning的名词

学习

从无数数据提供的E:experience中找到一个函数使得得到T:task后能够得到P:prediction

监督学习

experience中的数据都是有t和p的，计算机通过t和p得到函数

1.分类

p是明确的类 如：书有小说，教科书，故事书

2.回归

p是线性的，如：书的价格

非监督学习

experience中的数据只有t没有p，计算机仅通过t得到可以分成不同类的p函数

1.聚类

将产生的结果分成不同的集合，每个集合中的对象相似

二、单元线性回归方程与cost fnction

单元线性回归方程

单元 J() (cost function)

cost function的结果(训练拟合度)，越小拟合度越好

梯度下降算法与单元cost function

梯度下降算法

• alpha为学习速率
• 求J的偏导可以看出当前距离局部最低点远近程度
• theta_j为单元cost function中的参数，通过梯度下降法迭代调整参数，达到局部最低点

1.使用梯度下降法迭代

因为需要让J逐渐减小，所以要使用梯度下降

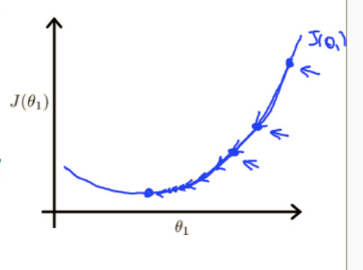
结合cost function和梯度下降算法（下图）

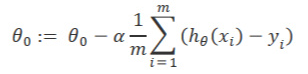
• iteration J中的所有参数应同时更新（下图）

• 我们常称x为feature（关联特征方程中的特征），h(x)为hypothesis

2.

alpha*J 得到的值并不是一个固定的值，随着迭代，J会越来越小接近0（拟合程度越来越好,下降的越少，逐渐接近局部最优解）

3.alpha也在不断变化

如果alpha无限大，虽然刚开始下降很快，但可能会遇到下图overshoot minimum现象这个问题，所以alpha在算法中应自适应调整

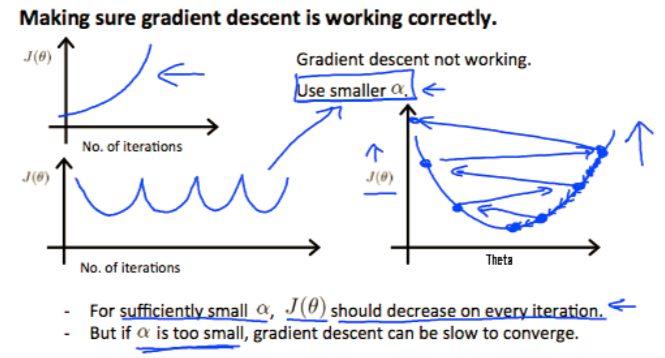
4. alpha 应如何调整

• 1.自动收敛法为根据J(theta)下降小于10^-3，则缩小alpha
• 2.调试收敛法，根据迭代次数，或者J（theta）上升了则需要下降alpha（如下图几种需要降低alpha）（推荐）
  

三、根据数据建立多元线性高次回归方程

1.样本表中得到信息

从图中可以得到信息：

• Y₁~X_n指输出变量
• X₁~X_n指样本变量，在h(theta)中为特征变量
• M：样本个数
• N：特征变量个数

2.多元一次线性回归方程

• theta指的是参数
• X₀默认0
• X₁~X_n指的是一组数据的n个特征变量
• 若有X⁽²⁾,(2)指的是第二个样本

3.特征缩放 feature scaling(重要)

当不同的特征值之间数据差距过大的时候，可能造成梯度下降很难到达最低点（这里不做介绍）
所以在使用h(theta)时，应先进行feature scaling

• 数据之间越接近下降越容易
• 数据应尽量缩小到-1和1左右（不要求很准确，（-3,3 ）（-1/3,1/3）都可以，但不能 太小如-0.001 或 太大如100）
• 常用方法：

   x'=\frac{x-a}{b}

a：{x}特征平均值

b：max(x)-min(x)或者方差

4.

当特征值有多个的时候，可以将特征值合并

例： 由房子的长宽特征预计价格，可以变为用房子的面积预计价格

5.

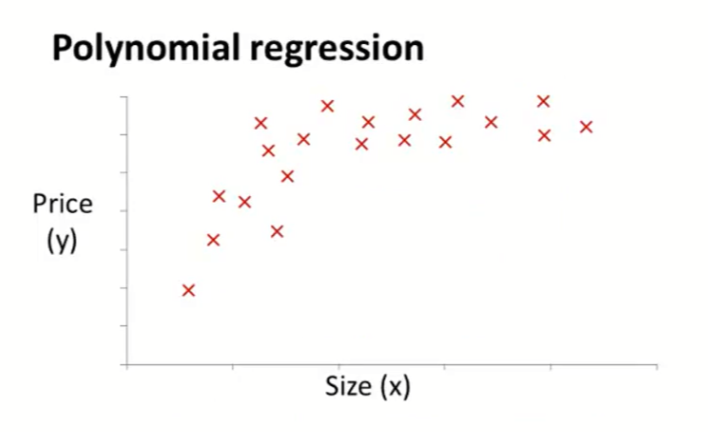
当样本数据如上图所示明显不符合线性，则使用高次的特征方程，如下图

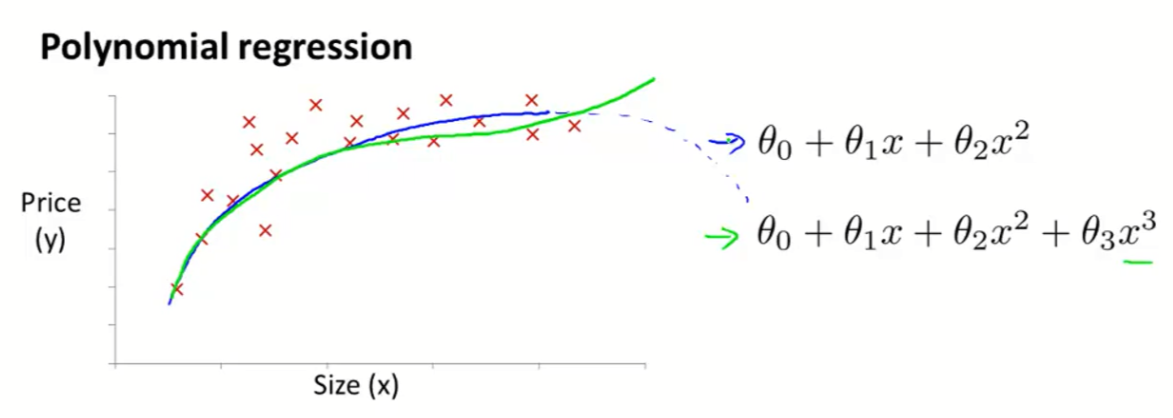
6.疑问

1. 两个特征值的合并是否一定要符合现实逻辑，比如长宽合成面积？
2. 如果结果就是需要长宽分别和价格之间的关系怎么办？
3. 上图中绿线是因为蓝线会在后方下降才改的，但没有数据的情况下谁都不能确定会是怎么样的，所以我觉得这样改没有意义，结果需要确定一个可预测价格范围（和给的数据样本差不多的范围）？
4. 是否只有在单一变量的时候才能将它化成有高次的特征方程？

四、 多元线性回归与梯度下降

1. 多元cost function

• 可以看下图，这两个式子等价于上式

2.结合特征方程和cost function

• 将多元特征方程带入cost function可得到拟合程度J(theta)

3.多元情况下 梯度下降方程

4.

• 和单元一样，多元也要同时更新
• 可以观察一下theta₀可以发现由于X₀=1,所以theta0式子和单元情况下一样

五、正规方程(normal equation)

除了梯度下降法的另一种方法，也可以找到局部最优解

正规方程

\theta = (X^T X)^{-1}X^T Y

计算步骤

• 从表格中提取信息

	Size(feet2)	Number of bedrooms	Number of floors	Age of house(years)	Price(*1000)
x0	x1	x2	x3	x4	y
1	2104	5	1	45	460
1	1416	3	2	40	232
1	1534	3	2	30	315
1	852	2	1	36	178

• 化成矩阵形式

• 代入正规方程

比较梯度下降和正规方程优劣势

梯度下降	正规方程
需要选择α	不需要选择α
需要许多迭代	不需要迭代
O(KN2)	O(N3)，需要计算逆矩阵XTX
当N较大时工作正常	如果N非常大会很慢

当n<10,000时,适合用正规方程
矩阵不可逆没关系，octave会算出伪逆，结果是一样的