Algorithm: 负环暴论 - 0
题解 P3385 负环
转载: https://www.luogu.me/article/0betmrit
\(\rightarrow\)题目传送门
我来写篇总结附带求出具体负环的吧。
题解:判断负环
既然判断负环的几种方法其他题解都已经提到过,那我就姑且只大概做个总结吧。
- Floyd 算法求负环,时间复杂度 \(\mathcal O (n^3)\):
可以考虑建立原图的反向图记录 \(1\) 向每个点的最短路径的更新来源再从点 \(1\) 开始 dfs 看是否能进入环中。
此外因为 Floyd 的结果中负环上的点到自身距离小于 \(0\),所以可以同时传下闭包(Floyd 一遍以后再从 \(1\) 开始 dfs 一遍判断可达点到自身的距离是否有小于 \(0\) 的也可)。
本题中由于时间复杂度太高而不能通过。
代码(自身距离+闭包):
int dis[MAXN][MAXN];
bool vis[MAXN][MAXN];
bool Floyd(int s)
{
vis[s][s]=1;
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
vis[i][j]|=vis[i][k]&&vis[k][j];
if(dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=dis[i][k]+dis[k][j];
}
for(int i=1;i<=n;i++)
if(vis[s][i]&&dis[i][i]<0)
return 1;//存在负环
return 0;
}
//读入&初始化
memset(dis,0x3f,sizeof(dis));//不能0x7f
memset(vis,0,sizeof(vis));
cin>>n>>m;
for(int i=1;i<=n;i++)
dis[i][i]=0,
vis[i][i]=0;
for(int i=0,u,v,w;i<m;i++)
{
cin>>u>>v>>w;
dis[u][v]=min(dis[u][v],w);
vis[u][v]=1;
if(w>=0)
vis[v][u]=1,
dis[v][u]=min(dis[v][u],w);
}
- SPFA 算法求负环,时间复杂度 \(\mathcal O (kn)\):
没有负环的图中一个最多被其他 \(n-1\) 个点松弛 \(n-1\) 次,如果一个点被从 \(1\) 出发的 SPFA 松弛了 \(n\) 次及以上,则存在由 \(1\) 可达的负环。
需要注意的一点是(如果有人之前学的 SPFA 像我学的一样),不同于求最短路时,这里如果在松弛完点 \(u\) 的可松弛边后才标记 \(u\) 出队,就会忽略掉由自环形成的负环。
代码:
int cnt[MAXN],dis[MAXN];
queue<int>q;
bool vis[MAXN];
int spfa(int s)
{
memset(vis,0,sizeof(vis));
memset(dis,0x7f,sizeof(dis));
memset(cnt,0,sizeof(cnt));
while(!q.empty())
q.pop();
vis[s]=1;
dis[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();
vis[u]=0;
q.pop();
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
if(!vis[v])
{
if(++cnt[v]>n)
return 1;
q.push(v);
vis[v]=1;
}
}
}
}
return 0;
}
- DFS-SPFA 求负环,时间复杂度 \(\mathcal O (n^2)\):
据说只是判断负环的话很快,但要求解的话很慢。
可以搜索实现,松弛到还未退出的点即存在负环。
也可以像这样把普通 SPFA 里的队列改为栈,模拟深搜,但要注意这时 vis[] 表示的是否正在搜索经过而非是否在栈内。
作为“SPFA”一如既往地容易被卡(此题中被 #9 卡)。
代码(其实这个模拟但没完全模拟,反而显得麻烦了):
int dis[MAXN];
int stk[MAXN],sp;
int pre[MAXN],cnt[MAXN];//从哪个点搜过来的 / 从一个点出发的搜索分支数
bool vis[MAXN],instk[MAXN];
int dfs_spfa(int s)
{
memset(vis,0,sizeof(vis));
memset(dis,0x7f,sizeof(dis));
memset(cnt,0,sizeof(cnt));
memset(instk,0,sizeof(instk));
sp=0;
stk[++sp]=s;
dis[s]=0;
instk[s]=1;
while(sp)
{
int u=stk[sp--];instk[u]=0;
vis[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].v;
if(dis[v]>dis[u]+e[i].w)
{
dis[v]=dis[u]+e[i].w;
if(vis[v])
return 1;
if(!instk[v])
stk[++sp]=v,
cnt[u]++,
pre[v]=u,
instk[v]=1;
}
}
while(u&&cnt[u]==0)
{
vis[u]=0;
u=pre[u];
cnt[u]--;
}
}
return 0;
}
- Bellman-Ford 算法求负环,时间复杂度 \(\mathcal O (mn)\):
即 SPFA 算法的本质。
Bellman-Ford 算法在没有负环时,最坏情况(一条链)下也只需 \(n-1\) 次即可完成所有松弛操作找到最短路,如果第 \(n\) 次仍有可松弛的边,则图中有负环。
但是它并不能直接判断是否由 \(1\) 可达,可以考虑第 \(n\) 次循环来一次万能的 dfs 或者在松弛时顺带传下闭包。
代码:
int dis[MAXN],vis[MAXN];
int bellman_ford(int s)
{
memset(dis,0x7f,sizeof(dis));
memset(vis,0,sizeof(vis));
dis[s]=0;
vis[s]=1;
for(int i=1;i<n;i++)
{
bool flag=1;
for(int j=1;j<=tot;j++)//tot:边数
if(dis[e[j].v]>dis[e[j].u]+e[j].w)
{
dis[e[j].v]=dis[e[j].u]+e[j].w;
vis[e[j].v]|=vis[e[j].u];
flag=0;
}
if(flag)
return 0;
}
for(int j=1;j<=tot;j++)
if(dis[e[j].v]>dis[e[j].u]+e[j].w)
{
dis[e[j].v]=dis[e[j].u]+e[j].w;
if(vis[e[j].u])
return 1;
}
return 0;
}
此外,本题中还有一点值得注意的就是,本题是一道个测试点有多组数据点的图论题,因此要重置链式向前星的 head[] 数组和加边计数(之前自己居然犯了这种错误……)。
说起来缩点暴力把边权变点权求负环似乎可能因正环加负环构成的 \(8\) 形图而不通用?类似下图:(有其他方法欢迎评论指出)
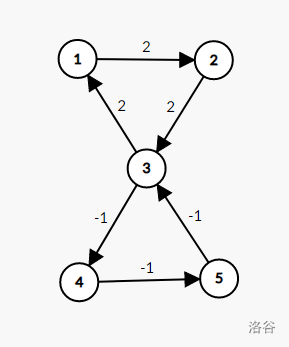
扩展:求出负环
虽然好像使用价值不是很大(总不能用负环缩点吧)。
- Floyd 算法:
上面求负环的前一种方案显然可以直接求出。
或者由上面提到的结论,哪些点在负环上一目了然。如果要分出每个点所在的负环,考虑 dfs。
- SPFA(Bellman-Ford)算法:
这里不再分开介绍。
在松弛时记录最短路径来源(SPFA 的话也可 DFS-SPFA 实现),回溯到环上 dfs。
值得注意的是 SPFA 中 cnt[v]>n 的点 \(v\) 和 Bellman-Ford 算法中第 \(n\) 次可松弛的边 \(i\) 不一定在负环上(如下图),因此需向前回溯 \(n\) 次。
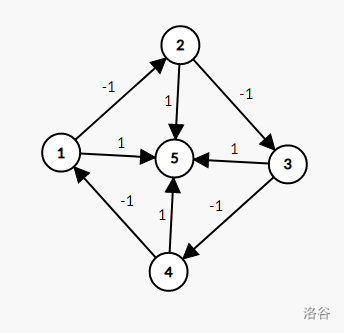
不过上面提到的几种方法,多半可能在两个负环构成的 \(8\) 形图中漏解,这个问题个人暂时无解 emmmm。
此外还在网上看到另一种建立“最短路径树”判环的方法,想了解的可以参考链接。
其他
关于上文提到的“Floyd 算法结果中负环上的点到自身距离小于 \(0\)”这个结论,个人的理解是:Floyd 最外层经过 \(k\) 次插点循环的结果是,最多经过 \(1 \cdots k\) 的点下的最短路径,如果存在负环,即便以及不满足动态规划的最优化原理,但自己到自己的距离会被一条经过负环至少一圈(一部分)的路径取代,因此负环上的点到自身距离小于 \(0\)。
如有不对或有其他更严谨/更好理解的想法欢迎指出,其他地方也是。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号