梯度下降

1.梯度下降(单，多元)

2.特征缩放

3.选择合适的α（学习率）

4.特征和多项式

 

梯度下降是很常用的算法，不仅用于线性回归，还广泛应用于机器学习的众多领域，可以最小化其他函数（任意函数）

 

 

不同的起始点有可能得到不同的局部最优解

 

 

 

 

 

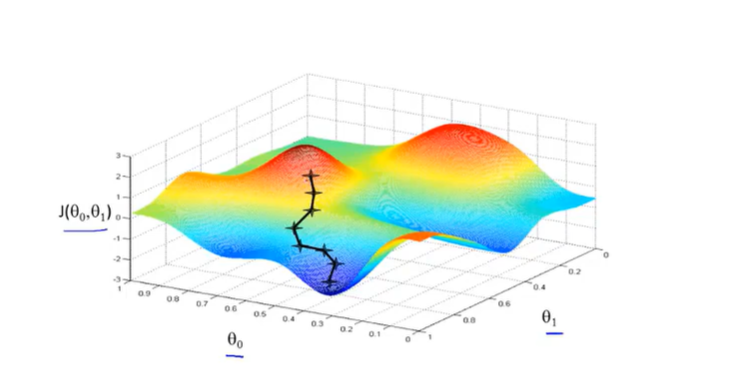
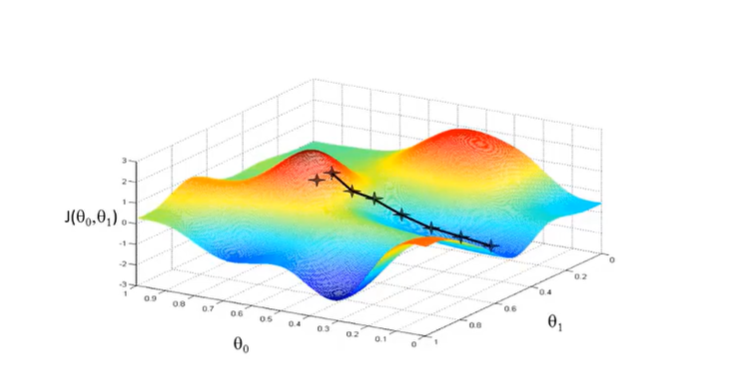
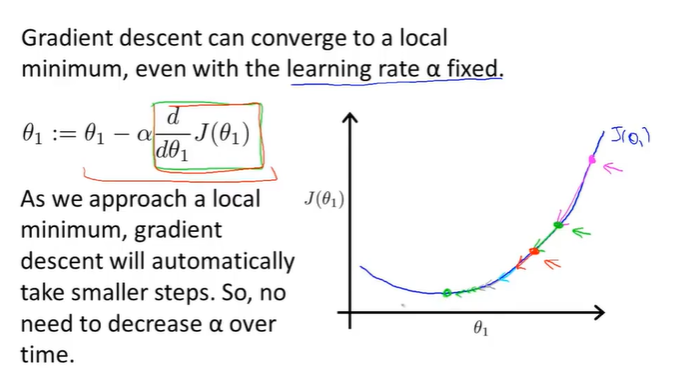
下图Θ逐渐减小，直到最佳状态

 

 

 

 

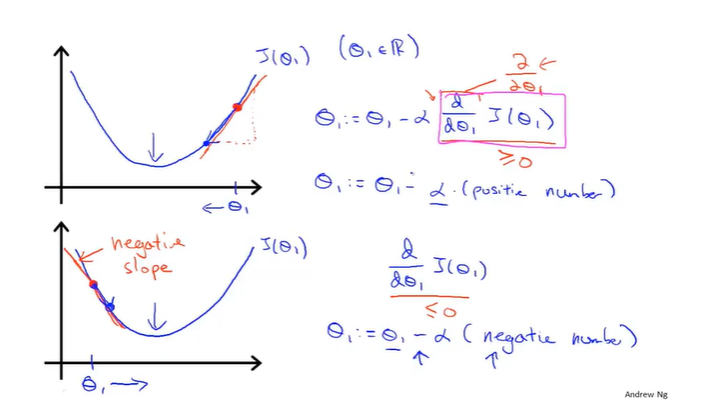
 可能会出现的问题

 

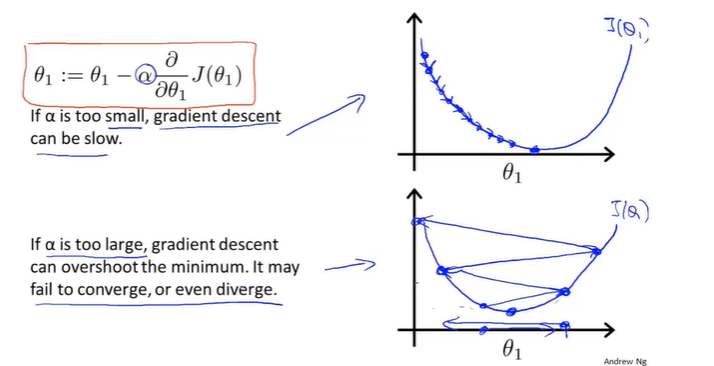
 随着导数斜率越来越小，下降的越来越慢

 

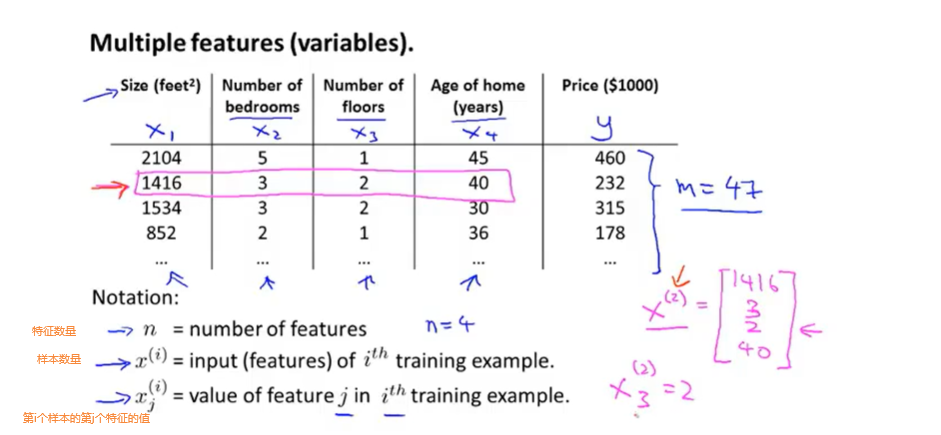
 多特征的时候

 

 

 

 

 

 

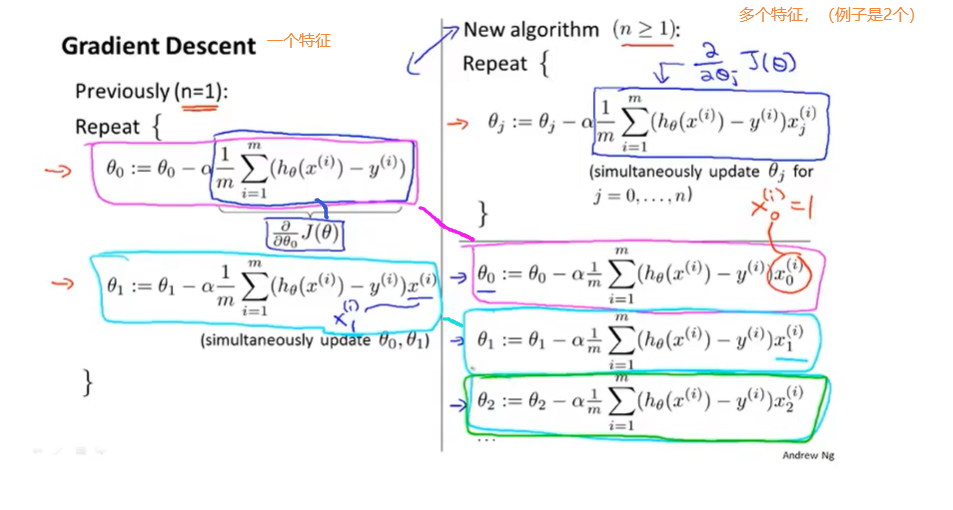
 单个特征对比多个特征（多元线性回归）

 

 

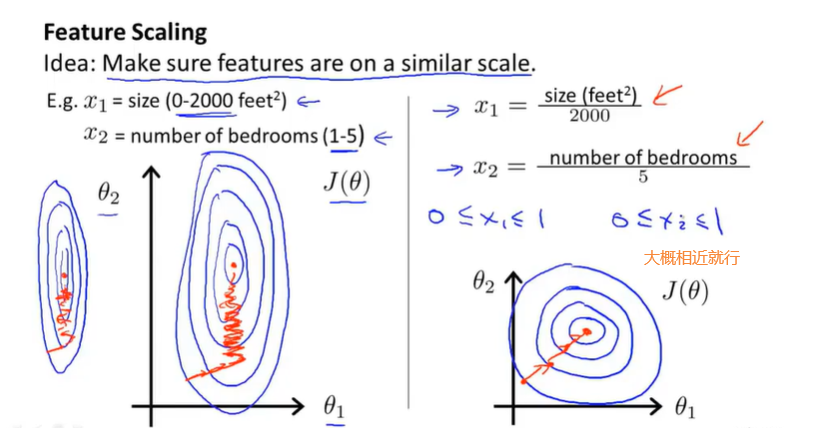
 特征缩放（将特征的值转换为相近似的范围）

 

 

 

 

也可以运用均值归一化

 如何选择合适的α（学习率）

不同问题的梯度下降达到收敛的迭代次数不同（最好可以通过看对应图来观察是否收敛）

 

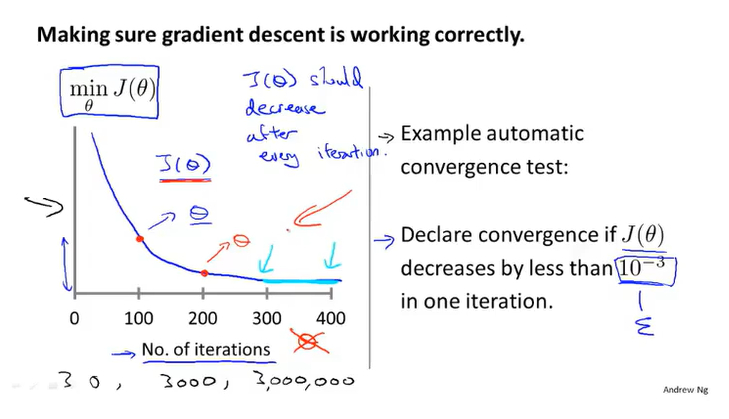
 α过大的话可能会出现J（α）异常上升或者波动的情况，解决办法就是减小α，但是α不能太小（不然下降会特别慢）

try     0.001,  0.01 , 0.1 等等  0.003 ，0.03 ， 0.3....等等都行

 特征和多项式

多次项拟合程度不好的话，可以试一试选择不同的特征，有时可以得到更好的模型