马尔科夫模型

   马尔可夫过程（Markov process）是一类随机过程。由俄国数学家A.A.马尔可夫于1907年提出。该过程具有如下特性：在已知目前状态（现在）的条件下，它未来的演变（将来）不依赖于它以往的演变 (过去 )。

一个马尔科夫过程就是指过程中的每个状态的转移只依赖于之前的 n个状态，这个过程被称为 n阶马尔科夫模型，其中 n是影响转移状态的数目。最简单的马尔科夫过程就是一阶过程，每一个状态的转移只依赖于其之前的那一个状态，这也是后面很多模型的讨论基础，很多时候马尔科夫链、隐马尔可夫模型都是只讨论一阶模型，甚至很多文章就将一阶模型称之为马尔科夫模型，现在我们知道一阶只是一种特例而已了。

对于一阶马尔科夫模型，则有：

如果第 i 时刻上的取值依赖于且仅依赖于第 i−1 时刻的取值，即

 

 

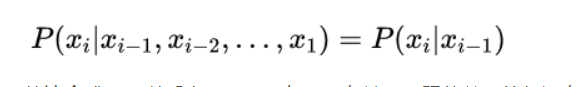
​ 从这个式子可以看出，xi 仅仅与 xi-1有关，二跟他前面的都没有关系了，这就是一阶过程。

总结：马尔科夫过程指的是一个状态不断演变的过程，对其进行建模后称之为马尔科夫模型，在一定程度上，马尔科夫过程和马尔科夫链可以打等号的。

 

1.2 马尔科夫性（无后效型）

在马尔科夫过程中，在给定当前知识或信息的情况下，过去（即当前以前的历史状态）对于预测将来（即当前以后的未来状态）是无关的。这种性质叫做无后效性。简单地说就是将来与过去无关，只与现在有关，不断向前形成这样一个过程。

————————————————
版权声明：本文为CSDN博主「LoveMIss-Y」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_27825451/article/details/100117715