Classification of time series by shapelet transformation[论文阅读1]

1 摘要

　“如何测量序列间的相似度”是时间序列分类(TSC)问题的挑战。Shapelet是时间序列的子序列，它是基于局部，无关相位的形状相似性进行TSC。基于Shapelet的分类是利用Shapelet和序列之间的相似性作为区分特征。Shapelet的优势之一：可解释性。原始的基于Shapelet的分类器将Shapelet发现算法嵌入到决策树中，并使用信息增益获取评估候选质量，并通过枚举搜索找到树的每个节点的Shapelet。随后的研究主要集中于技术的高效性。本文研究如何最好的使用Shapelet原型去构造分类器。本文提出一种single-scan（单扫描）Shapelet的算法寻找最佳的k个Shapelets，该算法用于生成数据转换后的数据集，其中k个特征中的每一个特征代表着一个时间序列到一个Shapelet的距离。与嵌入式方法相比，主要优势是：可以将转换后的数据与任何分类器结合使用，并且无需对Shapelet进行递归搜索。本文证实，转换后的数据可连接更复杂的分类器，在精度上比基于Shapelet的决策树更高。本文还对比了三种相似性度量，其可以在更短的时间内产生与信息增益相同的结果。实验结果表明，通过对Shapelet进行转换后聚类，可以增强转换后数据的可解释性。

2 背景介绍

2.1 时间序列分类(TSC)

　　假设有一时间序列集合T={T₁,T₂,...,T_n}，其中任一时间序列T_i有m个有序实值(T_i=<t_i,1,t_i,2,...,t_i,m>)和一个类标签C_i，假设所有时间序列T长度为m。时间序列分类问题就是找到了一个将时间序列空间映射到类值空间的函数。典型的有分辨相似性的特征有三种，分别为correlation-based（基于相关性）、autocorrelation-based（基于互相关性）和shape-based（基于形状）。本文主要关注于基于形状捕获相似性。

　　加入函数fc表示类别C的形状，那么一个时间序列可以表示为t_i,j=f_ci(j,s_i)+aj，其中s_i是序列i的偏移量，aj是噪声。基于形状的相似性又可以划分为全局相似和局部相似两种。全局相似定义为f_ci(j,s_i)=sin(j+s/ci*pi)。局部相似定义为f_ci(j,s_i)=sin(j/ci*pi),当s≤j＜s+l，其中l代表形状的长度，否则f_ci(j,s_i)=0。

2.2 Shapelet

　　shapelet是一个时间序列的子序列并且作为一个候选片段。Shapelet定是通过详尽的搜索任意长度的候选集而得到。我们感兴趣探索局部相似性，所以Shapelet的大小和偏移必须是不变的。其发现过程如算法1所示。

 

算法1 选择Shapelet(时间序列T，最小值，最大值)

 

　　1-2.最优值和最优shapelet初始化

　　3.for  在[min,max]范围内  do

　　4.生成候选集
　　5.for  所有候选集 do

　　6.计算时间序列和候选集内片段距离

　　7.评估质量

　　8-10.更新最优值和最优shapelet

　　11.返回最优shapelet

2.2.1 产生候选集

　　一个长度为m的时间序列包含了(m-l)+1个长度为l的候选片段。本文定义对于长度为l的时间序列Ti为W_i,L，所以可知W_l={W_1,l∪W_2,l∪...∪W_n,l}，由此可知W={W_min∪W_min+1∪...∪_Wmax}，当min≥3且max≤m。

2.2.2 Shapelet距离计算

设S和R的长度均为l，则S和R这两个子序列间的欧氏距离平方定义如下：

 

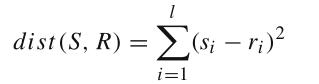
时间序列T_i与长度为l的子序列S之间的距离是S与T_i的所有归一化长度为l的子序列之间的最小距离：

 

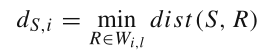
所以一个候选集合S和整个时间序列T之间的关系如下所示：

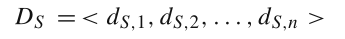
未完待续...