统计学习方法-第2章-感知机(1)

2.1 感知机模型

**定义: **输入特征空间为\(\chi\subseteq R^n\), 输出空间为\(\mathcal{Y}=\{+1, -1\}\). 则由输入空间到输出空间的如下函数:

\[f(x) = sign(w\cdot x+b) \]

其中$$sign(x)=\left{\begin{array}{cc}
+1, & x\geq 0\
-1, & x<0
\end{array}\right.$$
称为感知机. 是一种线性分类模型, 属于判别模型.
**几何解释: **线性方程\(w\cdot x+b=0\)对应特征空间\(R^n\)中一个超平面\(S\), 其中\(w\)为其法向量, \(b\)为其截距. 超平面\(S\)将特征空间划分为两部分, 位于两部分的特征向量被分为正负两类.

2.2 感知机学习策略

在介绍感知机的学习方法之前, 需要知道感知机学习的前提假设是数据集是线性可分的, 即存在某个超平面\(S\)能够将数据集的正负例点完全正确地划分开, 对于所有\(y_i = +1\)的实例\(i\)有\(w\cdot x_i + b>0\), 对于所有\(y_i = -1\)的实例\(i\)有\(w\cdot x_i + b<0\).


假设训练数据集是线性可分的, 感知机学习的目标是确定\(w\), \(b\)从而得到一个可以正确划分训练集正负样本的分离超平面, 需要定义损失函数并将其极小化. 感知机所采用的损失函数是误分类点到超平面\(S\)的总距离.
首先, 特征空间\(R^n\)中任意一点\(x_0\)到超平面\(S\)的距离:

\[d = \frac{1}{||w||} |w\cdot x_0 + b| \]

而对于误分类的点, 有\(-y_i(w\cdot x_i + b) > 0\), 所以, 误分类点\(x_i\)到超平面\(S\)的距离之和为:

\[-\frac{1}{||w||}\sum_{x_i\in M}{y_i(w\cdot x_i + b)} \]

其中\(M\)为超平面\(S\)误分类点集合. 忽略常数因子,得到感知机学习的损失函数为:

\[L(w,b)=-\sum_{x_i\in M}{y_i(w\cdot x_i + b)} \]

该损失函数就是感知机学习的经验风险函数, 显然\(L(w,b)\)是非负的, 若没有误分类点, 则损失函数为\(0\). 而且对于一个特定样本点的损失函数, 其在错误分类时是参数\(w\), \(b\)的线性函数, 在正确分类时为\(0\). 故损函数\(L(w,b)\)是\(w\), \(b\)的连续可导函数.

2.3 感知机学习算法

感知机学习问题转化为了求解损函数\(L(w,b)\)的最优化问题, 使用随机梯度下降法.

2.3.1 感知机学习算法的原始形式

**问题: **给定训练数据集\(T=\{(x_1, y_1), (x_2, y_2),...,(x_N, y_N)\}\), 其中\(x_i \in \chi = R^n,y_i\in \mathcal{Y}=\{+1, -1\},i=1,2,...,N\), 求参数\(w\), \(b\), 使其为以下故损失函数极小化问题的解

\[\min_{w,b}{L(w,b)=-\sum_{x_i\in M}{y_i(w\cdot x_i + b)}} \]

其中\(M\)为错误分类点的集合.
初始时, 任意选择一个超平面\(w_0\), \(b_0\), 然后每次随机选取一个误分类点使其梯度下降. 损失函数的梯度为

\[\begin{align*} \nabla_w L(w,b) &=-\sum_{x_i\in M}{y_i x_i}\\ \nabla_b L(w,b)&=-\sum_{x_i\in M}{y_i} \end{align*} \]

随机选择一个误分类点\((x_i, y_i)\), 对\(w\), \(b\)更新:

\[\begin{align*} w &\leftarrow w+\eta y_i x_i \\ b &\leftarrow b+\eta y_i \end{align*} \]

其中\(\eta(0<\eta \leq 1)\)是步长, 即学习率. 迭代算法如下:
**算法: **
输入: 训练数据集\(T=\{(x_1, y_1), (x_2, y_2),...,(x_N, y_N)\}\), 其中\(x_i \in \chi = R^n,y_i\in \mathcal{Y}=\{+1, -1\},i=1,2,...,N\), 学习率\(\eta(0<\eta \leq 1)\);
输出: \(w\), \(b\); 感知机模型\(f(x) = sign(w\cdot x+b)\).

1. 选取初值\(w_0\), \(b_0\)
2. 在训练数据中选取\((x_i, y_i)\)
3. 如果\(y_i(w \cdot x_i +b) \leq 0\)

\[\begin{align*} w &\leftarrow w+\eta y_i x_i \\ b &\leftarrow b+\eta y_i \end{align*} \]

4. 转到2, 直到训练集中没有误分类点.

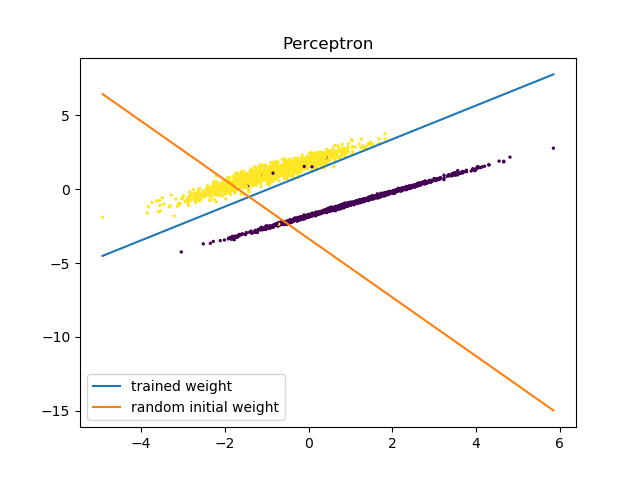
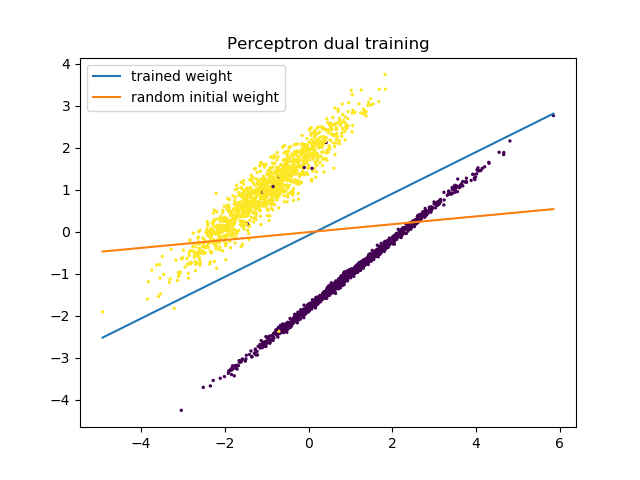
2.4 实现

python实现: eguilg/bluebook/perceptron