Qoj14432 Cyclic Topsort

我们注意到如果是对于 \(i\in[1,l]\) 都满足要求，那么这个东西就是一个拓扑序。

于是题目的要求说人话就是，在可以随便删掉一个点的情况下，我们可以得到的最长拓扑序是什么。

于是我们先把可以直接删掉的点处理掉，然后再在剩下的图里面跑。

如果 \(x\) 删除之后可以多删除 \(y\)，那么我们称 \(x\) 是可以到达 \(y\)。

有一个结论，如果 \(x\) 和 \(y\) 都可以到达 \(z\)，那么 \(x\) 一定是可以到 \(y\) 或者 \(y\) 一定是可以到 \(x\) 的。

我们可以使用反证法，假设上面的条件不成立，那么一定呈现一个下面的情况：

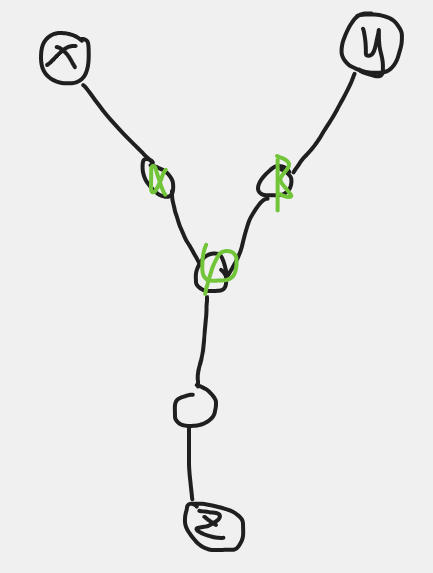
我们发现，如果 \(x\) 或者 \(y\) 不同时删除，\(z\) 是一定无法被删除的。

于是，我们注意到这个图现在形成了一个类似于树形结构的东西，于是有一种神器的算法。

我们每一次随机从一个点开始，向下走直到全部拓扑完。

如果开始的点是已经走过的点，那么我们就直接放弃，因为肯定没有遍历这个点的时候优。

这个东西的复杂度是 \(O(n\log n)\)，因为一个点只可能在包含树上由祖先访问，这相当于一个前缀 \(\max\) 的个数。