浅谈矩阵树定理的证明

注意：矩阵树定理支持重边，但不可以存在自环！！！

一些概念

主子式

定义一个有 \(k\) 个元素的集合 \(S\) 且所有元素都是 \([1,n]\) 中的整数，那么对于任意 \(i,j\in S\) 中将行列式 \(A_{n\times n}\) 中的 \(A_{i,j}\) 取出按 \((i,j)\) 的位置放入新的行列式。

最后得到的行列式中，将空缺的区域挤压掉得到的最后的有 \(k\times k\) 个元素的行列式就称其为矩阵 \(A\) 的 \(k\) 阶主子式。

举个例子，对于下面的矩阵，如果 \(S=\{1,3\}\) 那么变化就是这样的：

\[\begin{bmatrix} 1 & 2& 3& 4\\ 5 &6 & 7& 8\\ 9 & 10 & 11 & 12\\ 13 & 14 & 15 &16 \end{bmatrix}\Rightarrow \begin{bmatrix} 1 & & 3& \\ & & & \\ 9 & & 11 & \\ & & \end{bmatrix}\Rightarrow \begin{bmatrix} 1 &3 \\ 9 &11 \end{bmatrix}\]

余子式

定义一个数 \(k\in[1,n]\)，那么将行列式的 \(A_{n\times n}\) 的第 \(k\) 行和第 \(k\) 列删除之后剩余的 \((n-1)\times (n-1)\) 的行列式就是 \(A\) 的余子式。

举个例子，对于下面的矩阵，如果 \(k=2\) 那么变化就是这样的：

\[\begin{bmatrix} 1 & 2 &3 \\ 4 & 5 & 6\\ 7 & 8 &9 \end{bmatrix}\Rightarrow \begin{bmatrix} 1 & &3 \\ & & \\ 7 & &9 \end{bmatrix}\Rightarrow \begin{bmatrix} 1 & 3\\ 7 &9 \end{bmatrix}\]

转置矩阵

如果有 \(i\in[1,n],j\in[1,m]\)，对于矩阵 \(A_{n\times m}\) 和矩阵 \(B_{m\times n}\) 满足 \(A_{i,j}=B_{j,i}\)，那么定义 \(A=B^T\)。

无向图情况

假设有一个 \(n\) 个点的无向图 \(G\)，那么定义一下一些矩阵：

  • 定义度数矩阵 \(D_{n\times n}\)，其意义如下：

    \[D_{i,j}=\left\{\begin{matrix} \operatorname{deg}(i) &i=j \\ 0 & \operatorname{otherwise} \end{matrix}\right.\]

  • 定义 \(\#e(i,j)\) 便是 \((i,j)\) 之间的边的数量。

  • 定义边数矩阵 \(A_{n\times n}\)，其定义如下：

    \[A_{i,j}=\left\{\begin{matrix} \#e(i,j) & i\ne j \\ 0 & \operatorname{otherwise} \end{matrix}\right.\]

  • 定义基尔霍夫矩阵 \(L_{n\times n}\)，其定义为 \(L_{n\times n}=D_{n\times n}-A_{n\times n}\)。

  • 定义 \(t(G)\) 表示无向图 \(G\) 的生成树个数。

定理

对于无向图，对于 \(L\) 的任意 \(n-1\) 阶主子式的值都是相等的，且所有的值都是 \(t(G)\)。

证明

引理

引理 1

定义有 \(m\) 条边的无向图 \(G\) 的 \(M_{n\times m}\) 矩阵其意义如下：

\[M_{i,j}=\left\{\begin{matrix} -1 &\text{i is the end of the edge}_j \\ 1 &\text{i is the start of the edge}_j \\ 0 &\text{otherwise} \end{matrix}\right.\]

举个例子，对于下图：

.PNG

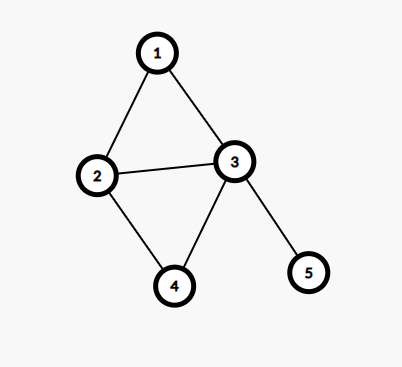
我们将所有的边随意指定一个方向得到：

.PNG

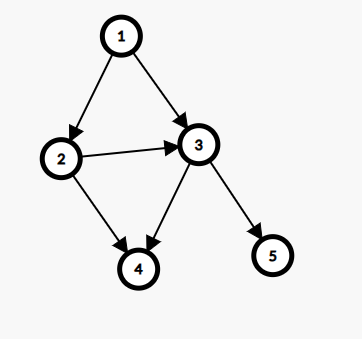
那么 \(M\) 矩阵就是下面的样子：

\[\begin{bmatrix} 1 & 1 & 0 & 0 & -1 &0 \\ -1 & 0 &1 &1 & 0 & 0\\ 0 & -1 & -1 & 0 & 1 &1 \\ 0 & 0 & 0 & -1 & 0 &0 \\ 0 & 0 & 0 & 0 & 0&-1 \end{bmatrix}\]

在一共有的 \(m\) 条边中选择出 \(n-1\) 条边，如果这个图联通那么这就是一个生成树。将这个操作对应到原来的矩阵 \(M\) 就相当于在 \(m\) 列中选出 \(n-1\) 列构成的 \(n\times (n-1)\) 的矩阵，我们称之为 \(M_0\)。

继续举上面的例子，在这个图中随便选择了 \(n-1\) 条边之后，就得到了下面的这个图：

1.PNG

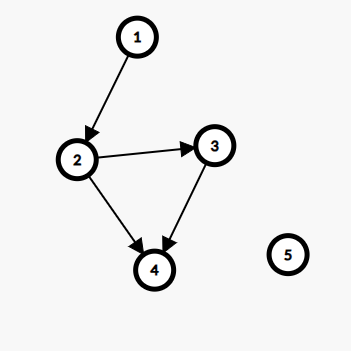
这个图的矩阵 \(M_0\) 就是下面：

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ -1 &1 &1 & 0 \\ 0 & -1 & 0 & 1 \\ 0 & 0 & -1 & -1 \\ 0 & 0 & 0 & 0 \end{bmatrix}\]

因为这个矩阵 \(M_0\) 是 \(n\times (n-1)\) 的不可以使用行列式求解，所以我们可以将 \(M_0\) 矩阵删掉一行得到矩阵 \(M_0^{'}\)。对于所有的选择 \(n-1\)条边的方法一共有两个可能性：构成一棵树和不构成一棵树。

对于不构成一棵树的情况必定至少有一个点是与任一点都不连通的，不妨设这个点的编号是 \(n\)。那么因为对于每一列的 \(1\) 和 \(-1\) 都对应这一条边，所以他们出现的数量应该是一样的，所以对于任意的 \(i\in[1,n-1]\) 一定有 \(\sum_{j=1}^{n-1}M_{i,j}=0\)。所以将上面的 \(n-1\) 行全部相加之后就得到了一个全 \(0\) 的一行，所以我们就得到了这个矩阵中的行是线性相关的，那么随意删除一条边是不会影响整个矩阵的。

举个例子，下面的不构成树的矩阵在将前 \(n-1\) 行加起来之后就得到了最后一行。

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ -1 &1 &1 & 0 \\ 0 & -1 & 0 & 1 \\ 0 & 0 & -1 & -1 \\ 0 & 0 & 0 & 0 \end{bmatrix}\]

对于构成一棵树的情况也同理。将这个矩阵所有的行全部相加，因为所有的 \(1\) 和 \(-1\) 都对应了原图中的一条边也就是他们都是成对出现的。形式化的，对于任意的 \(i\in[1,n-1]\) 一定有 \(\sum_{j=1}^{n}M_{i,j}=0\)。将前 \(n-1\) 行看作一个整体，因为其中的所有元素与第 \(n\) 行相加之后都得到了 \(0\)，那么所有的元素均互为相反数。所以我们也得到了这个矩阵中的行是线性相关的，那么随意删除一条边必然是不会影响整个矩阵的。

举个例子，将下面的矩阵的前 \(n-1\) 行相加就得到了最后一行的每个数都是相反数的一行。

\[\begin{bmatrix} 1 & 1 & 0 & 0 \\ -1 &0 &0 & 0 \\ 0 & -1& 1 & 1 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}\]

综上所述，将 \(M_0\) 转化为 \(M^{'}\) 是不会让元素丢失的。

引理 2

矩阵 \(M^{'}\) 有一个性质：\(\operatorname{det}(M^{'})\) 的值在 \(M^{'}\) 不构成树的情况下为 \(0\)，反之为 \(\pm 1\) 。

对于不构成树的情况 \(M^{'}\) 中必然存在一个简单环，那么将所有的构成环的行全部相加。如果刚好被删除了也没有关系，因为这是线性相关的，可以构造出来。那么因为在环上的所有点出现的次数都是一样的，所以在将环所包含的所有的点所在的行全部相加会得到两种情况。

如果所有的点都被包含在环中，那么在所有行相加之后一定所有的元素都是 \(0\)，所以将前 \(n-1\) 行看作一个整体，因为其中的所有元素与第 \(n\) 行相加之后都得到了 \(0\)，那么所有的元素均互为相反数。所以我们也得到了这个矩阵中的行是线性相关的，所以在高斯消元之后它的对角线会出现一个自由元也就是系数为 \(0\) 的情况，那么 \(\operatorname{det}(M^{'})\) 显然为 \(0\)。

如果不包含所有点的情况，将环中所有包含的点的那些行全部相加。因为这是一个简单环，所以就可以将环所包含的边的那几列全部消成 \(0\)，所以容易得到这个矩阵其实也是有自由元的整个矩阵的值为 \(0\)。

对于构成树的情况，叶子节点必然满足一行对应行只有一个非零元素。使对应行消去其他行，然后该非零元素对应的行列都只有其一个非零元素。在将全部为 \(0\) 的一行与一列删除之后又得到了新的一样的矩阵，在使用归纳法继续递归就可以最终得到只有一个元素且值为 \(\pm 1\) 的矩阵，所以 \(\operatorname{det}(M^{'})\) 必然等于 \(\pm 1\)。

引理 3

矩阵 \(M\) 还有一个性质：

\[M\times M^T=L \]

根据定义容易得到：

\[M_{i,j}\times {M^T}_{i,j}=\sum_{k=1}^{m}M_{i,k}\times {M^T}_{k,j} \]

根据 \(M^T\) 的定义得以推得：

\[M_{i,j}\times {M^{T}}_{i,j}=\sum_{k=1}^{m}M_{i,k}\times M_{j,k} \]

观察上面的式子容易得到只有 \(i,j\) 都是 \(k\) 这条边的端点时，\(M_{i,k}\times M_{j,k}\) 才不是 \(0\)。

  • 对于 \(i=j\) 的情况，\(M_{i,k}=M_{j,k}\) 所以可以写作 \({M_{i,k}}^2\) 显然无论 \(M_{i,k}\) 的正负答案都是 \(1\)，这对应着 \(\operatorname{deg}_{in}i\)。
  • 对于 \(i\ne j\) 的情况，\(M_{i,k}=-M_{j,k}\) 因为一条边的两点符号相反，所以 \(M_{i,k}\times M_{j,k}=-1\)，所以贡献肯定为 \(-1\)，这对应了 \(A_{i,j}\)。

引理 4（Binet-Cauchy）

定义大小分别为 \(n \times m, m \times n(n \le m)\) 的矩阵 \(A, B\) 则有：

\[\det(AB) = \sum\limits_{S \subseteq \{1, 2, \cdots m\}, |S| = n} \det(A[S]) \times \det(B[S]) \]

其中 \(A[S], B[S]\) 分别表示 \(A\) 取 \(S\) 集合内的列，\(B\) 取 \(S\) 集合内的行所构成的矩阵。

首先我们展开等式右侧：

\[\begin{aligned} & \sum\limits_{S \subseteq \{1, 2, \cdots m\}, |S| = n} \det(A[S]) \times \det(B[S]) \\ &= \sum\limits_{S \subseteq \{1, 2, \cdots m\}, |S| = n} \left(\sum\limits_{P} (-1) ^ {\lambda(P)} \prod\limits_{i = 1} ^ n A_{i, S_{P_i}}\right) \times \left(\sum\limits_{Q} (-1) ^ {\lambda(Q)} \prod\limits_{i = 1} ^ n B_{S_i, Q_i}\right) \\ &= \sum\limits_{S} \sum\limits_{P} \sum\limits_{Q} (-1) ^ {\lambda(P) + \lambda(Q)} \prod\limits_{i = 1} ^ n A_{i, S_{P_i}} \times B_{S_i, Q_i} \\ \end{aligned} \]

再展开等式左侧：

\[\begin{aligned} & \det(AB) \\ &= \sum\limits_{P} (-1) ^ {\lambda(P)} \prod\limits_{i = 1} ^ n \left(\sum\limits_{j = 1} ^ m A_{i, j} \times B_{j, P_i}\right) \\ &= \sum\limits_{P} (-1) ^ {\lambda(P)} \sum\limits_{R} \left(\prod\limits_{i = 1} ^ n A_{i, R_i} \times B_{R_i, P_i}\right) (|R| = n, \forall i, R_i \in \{1, 2, \cdots m\}) \\ &= \sum\limits_{R} \sum\limits_{P} (-1) ^ {\lambda(P)} \left(\prod\limits_{i = 1} ^ n A_{i, R_i}\right) \times \left(\prod\limits_{i = 1} ^ n B_{R_i, P_i}\right) \end{aligned} \]

仔细观察可知，对于可重排列 \(R\)，若存在 \(i < j, R_i = R_j\) 那么交换 \(P_i, P_j\) 后后面的积式不变，但逆序对奇偶性改变，因此两者贡献互为相反数可抵消。 因此我们只需钦定每个存在 \(i < j, R_i = R_j\) 的可重排列 \(R\)，让其和交换满足条件的最小 \(P_i, P_j\) 交换后的排列 \(P\) 的贡献相抵即可。 因为交换最小的 \(i, j\) 后依然满足 \(i, j\) 为最小的满足条件的点对，因此可以两两唯一配对。 故我们只需枚举不重的序列即可，为此我们首先枚举 \(\{1, 2, \cdots m\}\) 的子集，然后枚举一个长度为 \(n\) 的排列 \(Q\)：

\[\begin{aligned} & \det(AB) \\ &= \sum\limits_{S} \sum\limits_{Q} \sum\limits_{P} (-1) ^ {\lambda(P)} \prod\limits_{i = 1} ^ n A_{i, S_{Q_i}} \times B_{S_{Q_i}, P_i} \\ &= \sum\limits_{S} \sum\limits_{Q} \sum\limits_{P_{Q'}} (-1) ^ {\lambda(P_{Q'})} \left(\prod\limits_{i = 1} ^ n A_{i, S_{Q_i}}\right) \times \left(\prod\limits_{i = 1} ^ n B_{S_i, P_{Q'_i}}\right) \\ &= \sum\limits_{S} \sum\limits_{Q} \sum\limits_{P_{Q'}} (-1) ^ {\lambda(P) + \lambda(Q)} \left(\prod\limits_{i = 1} ^ n A_{i, S_{Q_i}}\right) \times \left(\prod\limits_{i = 1} ^ n B_{S_i, P_{Q'_i}}\right) \end{aligned} \]

整理即可得到从右侧推导得到的式子。

定理证明

记 \(L\) 的 \(n-1\) 阶主子式为 \(L_0\)，那么根据引理3可以得到：

\[\det(L_0)=\det(M^{'}\times {M^{'}}^T) \]

根据引理4可以得到：

\[\det(L_0)=\sum_{S\subseteq \{1,2,\cdots,m\wedge|S|=n-1\}}\det M^{'}\times \det {M^{'}}^T \]

化简可以得到：

\[\det(L_0)=\sum_{S\subseteq \{1,2,\cdots,m\wedge|S|=n-1\}}(\det M^{'})^2 \]

容易发现其中的 \(S\) 就是选边的方案，如果合法那么 \(\det^2\) 就是 \(1\) 反之即为 \(0\)。

显而易见的，这就是生成树的个数。

叶向生成树情况

假设有一个 \(n\) 个点的有向图 \(G\)，那么定义一下一些矩阵：

  • 定义度数矩阵 \(D_{n\times n}\)，其意义如下：

    \[D_{i,j}=\left\{\begin{matrix} \operatorname{deg_{in}}(i) &i=j \\ 0 & \operatorname{otherwise} \end{matrix}\right.\]

  • 定义 \(\#e(i,j)\) 是 \((i\to j)\) 边的数量。

  • 定义边数矩阵 \(A_{n\times n}\)，其定义如下：

    \[A_{i,j}=\left\{\begin{matrix} \#e(i,j) & i\ne j \\ 0 & \operatorname{otherwise} \end{matrix}\right.\]

  • 定义基尔霍夫矩阵 \(L_{n\times n}\)，其定义为 \(L_{n\times n}=D_{n\times n}-A_{n\times n}\)。

  • 定义 \(t(G)\) 表示有向图 \(G\) 的叶的生成树个数。

定理

对于无向图，对于 \(L\) 的任意 \(n-1\) 阶主子式的值都是相等的，且所有的值都是 \(t(G)\)。

证明

定义有 \(m\) 条边的有向图 \(G\) 的 \(M_{n\times m}\) 矩阵其意义如下：

\[M_{i,j}=\left\{\begin{matrix} -1 &\text{i is the end of the edge}_j \\ 1 &\text{i is the start of the edge}_j \\ 0 &\text{otherwise} \end{matrix}\right.\]

定义矩阵 \(D_{n\times m}\) 的意义如下：

\[D_{i,j}=\left\{\begin{matrix} 1 &e_j\text{是}v_i\text{的入边} \\ 0 &\text{otherwise} \end{matrix}\right.\]

经过观察容易得到 \(L=M\times D^T\)。

根据定义可以得到：

\[M_{i,j}\times {D^T}_{i,j}=\sum_{k=1}^m M_{i,k}\times {D^T}_{k,j} \]

根据 \(D^T\) 的定义可以得到：

\[M_{i,j}\times {D^T}_{i,j}=\sum_{k=1}^m M_{i,k}\times D_{j,k} \]

经过观察可以得到，对于一个 \(k\) 这条边只有满足 \(i,j\) 都是它的端点才有贡献。

  • 对于 \(i=j\) 的情况，\(M_{i,k}=D_{j,k}\)，所以可以写作 \({M_{i,k}}^2\) 答案显然是 \(1\)，这对应着 \(\operatorname{deg}_{in}i\)。

  • 对于 \(i\ne j\) 的情况，\(M_{i,k}=-D_{j,k}\)，所以贡献肯定为 \(-1\)，这对应了 \(A_{i,j}\)。

参考资料：

posted @ 2025-09-26 14:34  未抑郁的刘大狗  阅读(5)  评论(0)    收藏  举报