省选测试39
总结
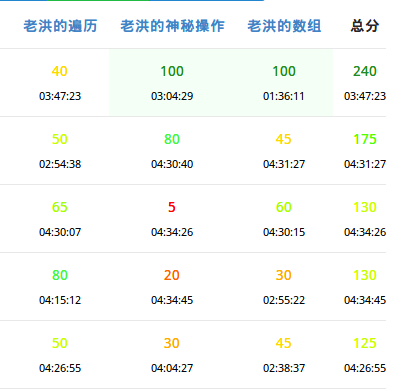

时间都花到 \(T1\) 上了,不过也拿到了该拿的分。
A. 老洪的遍历
分析
暴力的做法是按照 \(B\) 的值排序后,去枚举起点和终点,选出一个贡献最大的子序列和一个贡献最小的子序列,答案就是两者之差。
发现直接强制以 \(1\) 为起点和以 \(n\) 为终点一定是最优的,因为可以同一条边正反走两次把它们的贡献抵消成 \(0\)。
对于 \(|A_i|=1\) 的部分分,建出凸包后直接二分斜率找最大最小值。
满分的做法把贡献的式子拆成了 \(\frac{1}{2}(\frac{B_j}{A_j}B_i-B_j\frac{B_i}{A_i})\),
如果把 \(B_i\) 看成横坐标,\(\frac{B_i}{A_i}\)看成横坐标,那么就是一个叉积的形式。
找到凸包之后求面积即可。
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#define rg register
template<typename T>void read(rg T& x){
x=0;rg int fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
x*=fh;
}
const int maxn=1e5+5;
const double eps=1e-12;
struct Node{
double x,y;
Node(){}
Node(rg double aa,rg double bb){
x=aa,y=bb;
}
friend Node operator -(const Node& A,const Node& B){
return Node(A.x-B.x,A.y-B.y);
}
friend double operator ^(const Node& A,const Node& B){
return A.x*B.y-B.x*A.y;
}
}p[maxn],sta[maxn];
int n,tp,a[maxn],b[maxn];
double getdis(rg Node aa,rg Node bb){
return sqrt((aa.x-bb.x)*(aa.x-bb.x)+(aa.y-bb.y)*(aa.y-bb.y));
}
bool cmp(rg Node aa,rg Node bb){
rg double nans=(aa-p[1])^(bb-p[1]);
if(nans>eps) return 1;
else if(std::fabs(nans)<=eps) return getdis(aa,p[1])<getdis(bb,p[1]);
else return 0;
}
int main(){
read(n);
for(rg int i=1;i<=n;i++) read(a[i]);
for(rg int i=1;i<=n;i++) b[i]=b[i-1]+a[i];
for(rg int i=1;i<=n;i++){
p[i].x=1.0*b[i],p[i].y=1.0*b[i]/a[i];
if(p[i].y<p[1].y || (p[i].y==p[1].y && p[i].x<p[1].x)) std::swap(p[1],p[i]);
}
sta[tp=1]=p[1];
std::sort(p+2,p+1+n,cmp);
for(rg int i=2;i<=n;i++){
while(tp>1 && ((p[i]-sta[tp])^(sta[tp]-sta[tp-1]))>-eps) tp--;
sta[++tp]=p[i];
}
sta[tp+1]=sta[1];
rg double nans=0;
for(rg int i=1;i<=tp;i++){
nans+=(sta[i]^sta[i+1]);
}
printf("%.5f\n",nans/2);
return 0;
}
B. 老洪的神秘操作
分析
一个套路的做法就是转一下差分。
问题就变成了在一个位置加上一个数,在另一个位置减去一个数,最少多少次序列都变成 \(0\)。
发现 \(1\) 和 \(6\) ,\(2\) 和 \(5\),\(3\) 和 \(4\) 去配对一定是最优的,那么最终匹配完成后只会剩下 \(3\) 种。
大力 \(dp\) 求出剩下的值能够凑成多少组。
代码
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<iostream>
#define rg register
template<typename T>void read(rg T& x){
x=0;rg int fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
x*=fh;
}
const int maxn=505;
int n,a[maxn],cf[maxn],ans,num[maxn],f[maxn][maxn][maxn],rk[maxn],cnt;
int dfs(rg int now1,rg int now2,rg int now3){
if(!now1 && !now2 && !now3) return 0;
if(f[now1][now2][now3]) return f[now1][now2][now3];
rg int nans=0;
for(rg int i=now1;i>=std::max(0,now1-7);i--){
for(rg int j=now2;j>=std::max(0,now2-7);j--){
for(rg int k=now3;k>=std::max(0,now3-7);k--){
if(i==now1 && j==now2 && k==now3) continue;
if(((now1-i)*rk[1]+(now2-j)*rk[2]+(now3-k)*rk[3])%7==0) nans=std::max(nans,dfs(i,j,k)+1);
}
}
}
return f[now1][now2][now3]=nans;
}
int main(){
read(n);
for(rg int i=1;i<=n;i++) read(a[i]);
for(rg int i=1;i<=n;i++) cf[i]=a[i]-a[i-1];
for(rg int i=1;i<=n;i++) if(cf[i]<0) cf[i]+=7;
for(rg int i=1;i<=n;i++) num[cf[i]]++;
rg int tmp=std::min(num[1],num[6]);
num[1]-=tmp,num[6]-=tmp;
ans+=tmp;
tmp=std::min(num[2],num[5]);
num[2]-=tmp,num[5]-=tmp;
ans+=tmp;
tmp=std::min(num[3],num[4]);
num[3]-=tmp,num[4]-=tmp;
ans+=tmp;
for(rg int i=1;i<=6;i++){
if(num[i]) rk[++cnt]=i;
}
printf("%d\n",ans+num[rk[1]]+num[rk[2]]+num[rk[3]]-dfs(num[rk[1]],num[rk[2]],num[rk[3]]));
return 0;
}
C. 老洪的数组
分析
不难发现对于 \(f(x,y)\) ,\(C_j\) 对其系数的贡献是从 \((1,j)\) 走到 \((x,y)\) 的方案数。
对于询问分块,当修改的数量大于等于块长对于整体更新答案,否则就暂时存一下。
代码
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<iostream>
#define rg register
template<typename T>void read(rg T& x){
x=0;rg int fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
x*=fh;
}
const int maxn=2e5+5,mod=1e9+7;
inline int addmod(rg int now1,rg int now2){
return now1+=now2,now1>=mod?now1-mod:now1;
}
inline int delmod(rg int now1,rg int now2){
return now1-=now2,now1<0?now1+mod:now1;
}
inline int mulmod(rg long long now1,rg int now2){
return now1*=now2,now1>=mod?now1%mod:now1;
}
struct jie{
int x,y;
jie(){}
jie(rg int aa,rg int bb){
x=aa,y=bb;
}
}q[maxn];
int f[25][maxn],a[maxn],n,m,blo,jc[maxn],jcc[maxn],ny[maxn],tot,lst;
int getC(rg int nn,rg int mm){
return mulmod(jc[nn],mulmod(jcc[mm],jcc[nn-mm]));
}
void pre(){
ny[1]=1;
for(rg int i=2;i<=n+20;i++) ny[i]=mulmod(mod-mod/i,ny[mod%i]);
jc[0]=jcc[0]=1;
for(rg int i=1;i<=n+20;i++){
jc[i]=mulmod(jc[i-1],i);
jcc[i]=mulmod(jcc[i-1],ny[i]);
}
}
void build(){
for(rg int i=1;i<=n;i++) f[0][i]=a[i];
for(rg int i=1;i<=20;i++){
for(rg int j=1;j<=n;j++){
f[i][j]=addmod(f[i-1][j],f[i][j-1]);
}
}
}
int main(){
read(n),read(m);
for(rg int i=1;i<=n;i++) read(a[i]);
blo=sqrt(20*n);
pre(),build();
rg int aa,bb,cc,tmp;
for(rg int now=1;now<=m;now++){
read(aa),read(bb),read(cc);
if(aa==1){
q[++tot]=jie(bb,cc);
if(tot%blo==0){
for(rg int i=lst+1;i<=tot;i++) a[q[i].x]=q[i].y;
lst=tot;
build();
}
} else {
tmp=f[bb][cc];
for(rg int i=lst+1;i<=tot;i++){
if(q[i].x<=cc && q[i].x>=1) tmp=delmod(tmp,mulmod(a[q[i].x],getC(bb+cc-1-q[i].x,bb-1)));
std::swap(a[q[i].x],q[i].y);
if(q[i].x<=cc && q[i].x>=1) tmp=addmod(tmp,mulmod(a[q[i].x],getC(bb+cc-1-q[i].x,bb-1)));
}
for(rg int i=tot;i>=lst+1;i--) std::swap(a[q[i].x],q[i].y);
printf("%d\n",tmp);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号