省选测试8
总结

\(T1\) 送分题
\(T2\) 对偶图之前了解得不多,考场上也没有什么思路,不过 \(25\) 分暴力还是不应该丟的
\(T3\) 不会,\(5\) 分也没有打出来,没向 \(dp\) 方面去思考
A. GCD和LCM
分析
挺套路的,和数表那道题基本一样
离线下来用数状数组去维护就可以了
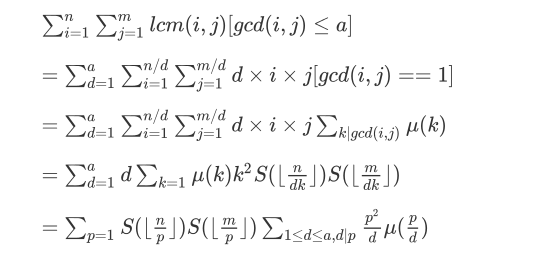
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int mod=1e9+7,maxn=1e5+5;
inline int addmod(rg int now1,rg int now2){
return now1+=now2,now1>=mod?now1-mod:now1;
}
inline int delmod(rg int now1,rg int now2){
return now1-=now2,now1<0?now1+mod:now1;
}
inline int mulmod(rg long long now1,rg int now2){
return now1*=now2,now1>=mod?now1%mod:now1;
}
int pri[maxn],mu[maxn],mmax,ny[maxn],sum[maxn];
bool not_pri[maxn];
int getsum(rg int now){
return mulmod(now,mulmod(now+1,ny[2]));
}
void xxs(){
not_pri[0]=not_pri[1]=1;
mu[1]=1;
for(rg int i=2;i<=mmax;i++){
if(!not_pri[i]){
pri[++pri[0]]=i;
mu[i]=mod-1;
}
for(rg int j=1;j<=pri[0] && i*pri[j]<=mmax;j++){
not_pri[i*pri[j]]=1;
if(i%pri[j]==0) break;
mu[i*pri[j]]=mod-mu[i];
}
}
ny[1]=1;
for(rg int i=2;i<=mmax;i++){
ny[i]=mulmod(mod-mod/i,ny[mod%i]);
}
for(rg int i=1;i<=mmax;i++) sum[i]=getsum(i);
}
int t,n,m,ans,nowans[maxn],a,tr[maxn];
int lb(rg int xx){
return xx&-xx;
}
void ad(rg int wz,rg int val){
for(rg int i=wz;i<=mmax;i+=lb(i)){
tr[i]=addmod(tr[i],val);
}
}
int cx(rg int wz){
rg int nans=0;
for(rg int i=wz;i>0;i-=lb(i)){
nans=addmod(nans,tr[i]);
}
return nans;
}
struct jie{
int nown,nowm,nowa,id;
}b[maxn];
bool cmp(rg jie aa,rg jie bb){
return aa.nowa<bb.nowa;
}
int main(){
mmax=1e5;
xxs();
t=read();
for(rg int i=1;i<=t;i++){
b[i].nown=read(),b[i].nowm=read(),b[i].nowa=read(),b[i].id=i;
}
std::sort(b+1,b+1+t,cmp);
rg int head=1;
for(rg int i=1;i<=t;i++){
n=b[i].nown,m=b[i].nowm,a=b[i].nowa;
if(n>m) std::swap(n,m);
while(head<=a){
for(rg int j=head;j<=mmax;j+=head){
ad(j,mulmod(j,mulmod(j,mulmod(ny[head],mu[j/head]))));
}
head++;
}
ans=0;
for(rg int l=1,r;l<=n;l=r+1){
r=std::min(n/(n/l),m/(m/l));
ans=addmod(ans,mulmod(mulmod(sum[n/l],sum[m/l]),delmod(cx(r),cx(l-1))));
}
nowans[b[i].id]=ans;
}
for(rg int i=1;i<=t;i++){
printf("%d\n",nowans[i]);
}
return 0;
}
B. 平面图
分析
平面图转对偶图
如果在对偶图中一条边两侧的点是自环
那么就会造成生成新的连通块
直接用并查集维护连通性即可
查询连通性操作用启发式分裂
当生成新的联通块时分开扫两个集合
扫到较小的那个就停止
然后给较小的那一块整体染上颜色
如果知道平面图上每个点所连的边的顺序
一个平面图转对偶图的方式是
考虑给每条边开两个对偶图上的节点
分别表示这条边左右对应的对偶图节点
对于一个点伸出的两条相邻的边
合并两个对偶图上节点
表示这两个节点实际上是一个节点
具体实现看代码就行了
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<unordered_map>
#include<vector>
#include<unordered_set>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=1e6+5;
int h[maxn],tot=2;
struct asd{
int to,nxt;
}b[maxn];
void ad(rg int aa,rg int bb){
b[tot].to=bb;
b[tot].nxt=h[aa];
h[aa]=tot++;
}
int fa[maxn],n,q,cnt,num[maxn],latans,scc,shuyu[maxn];
int zhao(rg int xx){
if(xx==fa[xx]) return xx;
return fa[xx]=zhao(fa[xx]);
}
long long getid(rg int i,rg int j){
return 1LL*i*n+j;
}
void bing(rg int aa,rg int bb){
aa=zhao(aa),bb=zhao(bb);
if(aa==bb) return;
fa[aa]=bb;
}
std::unordered_map<long long,int> mp;
std::vector<int> g[maxn];
std::unordered_set<int> s[maxn];
#define sit std::unordered_set<int>::iterator
void dfs(rg int now){
shuyu[now]=scc;
for(rg int i=h[now];i!=-1;i=b[i].nxt){
rg int u=b[i].to;
if(!shuyu[u]) dfs(u);
}
}
int q1[maxn],q2[maxn],h1,t1,h2,t2,tag,inq[maxn];
int main(){
memset(h,-1,sizeof(h));
n=read(),q=read();
rg int aa,bb;
for(rg int i=1;i<=n;i++){
num[i]=read();
for(rg int j=1;j<=num[i];j++){
aa=read();
mp[getid(i,aa)]=++cnt;
g[i].push_back(aa);
s[i].insert(aa);
if(i<aa) ad(i,aa),ad(aa,i);
}
}
for(rg int i=1;i<=cnt;i++) fa[i]=i;
for(rg int i=1;i<=n;i++){
for(rg int j=0;j<num[i];j++){
bing(mp[getid(i,g[i][j])],mp[getid(g[i][(j+1)%num[i]],i)]);
}
}
rg char ch;
for(rg int i=1;i<=n;i++){
if(!shuyu[i]){
scc++;
dfs(i);
}
}
rg sit it1,it2;
for(rg int i=1;i<=q;i++){
scanf(" %c",&ch);
aa=read(),bb=read();
aa^=latans,bb^=latans;
if(ch=='-'){
s[aa].erase(bb);
s[bb].erase(aa);
if(zhao(mp[getid(aa,bb)])==zhao(mp[getid(bb,aa)])){
scc++;
h1=t1=h2=t2=1;
q1[1]=aa,q2[1]=bb;
inq[aa]=inq[bb]=++tag;
it1=s[aa].begin(),it2=s[bb].begin();
while(h1<=t1 && h2<=t2){
while(h1<=t1){
if(it1==s[q1[h1]].end()) it1=s[q1[++h1]].begin();
else if(inq[*it1]==tag){
++it1;
continue;
} else {
inq[q1[++t1]=*it1]=tag;
++it1;
break;
}
}
while(h2<=t2){
if(it2==s[q2[h2]].end()) it2=s[q2[++h2]].begin();
else if(inq[*it2]==tag){
++it2;
continue;
} else {
inq[q2[++t2]=*it2]=tag;
++it2;
break;
}
}
}
if(h1>t1) for(rg int i=1;i<=t1;i++) shuyu[q1[i]]=scc;
else for(rg int i=1;i<=t2;i++) shuyu[q2[i]]=scc;
} else {
bing(mp[getid(aa,bb)],mp[getid(bb,aa)]);
}
printf("%d\n",latans=scc);
} else {
printf("%d\n",latans=(shuyu[aa]==shuyu[bb]));
}
}
return 0;
}
C. 路径
分析
题解的方法挺麻烦的
其实后面的部分可以直接用扩展卢卡斯的方法去处理
打表可以发现答案是一个式子
\(ans=\frac{f(n+m)}{f(n)f(m)}\)
其中 \(f(n)=\prod_{i=1}^n (q^i-1)\)
对于这个式子我们是不能直接去算逆元的
因为下面的部分在 \(\%p\) 意义下有可能为 \(0\)
所以我们应该把所有含 \(p\) 的项提出来
就像扩展卢卡斯那样
然后对于剩下的部分去求逆元
如果上面 \(p\) 的项多于下面 \(p\) 的项,那么答案就是 \(0\)
开始化简式子
\(f(n)=\prod\limits_{i=1}^{\frac{n}{k}} (q^{ik} -1)\prod\limits_{i=1,i \nmid k}^{n}(q^i-1)\)
右边那一部分直接记一个前缀和找循环节就行了
考虑化简左边
\(\prod\limits_{i=1}^{\frac{n}{k}}(q^{ik} -1)=(q^k -1)^{\frac{n}{k}} \prod\limits_{i=1}^{\frac{n}{k}} \sum\limits_{j=0}^{i-1} q^{kj}\)
把右边的那等比数列求和公式搞一下就能得到左边的
其中 \(\sum\limits_{j=0}^{i-1} q^{kj}=i\)
因为它的每一项都是一
其实就可以写成 \((q^k -1)^{\frac{n}{k}}\frac{n}{k}!\)
对于阶乘的那一部分,我们可以很容易地提出所有 \(p\) ,并且算出剩下的数是多少
对于左半部分,我们直接把它看成 \(p^{\frac{n}{k}}\) 即可
也就是说,令它的指数为 \(\frac{n}{k}\),系数为 \(1\)
简单地证明一下
这个式子对最终的分子答案的贡献是 \((xp^a)^{\frac{n+m}{k}}\)
对分母答案的贡献是 \((xp^a)^{\frac{n}{k}+\frac{m}{k}}\)
显然 \(\frac{n}{k}+\frac{m}{k} \leq \frac{n+m}{k}\)
如果 \(\frac{n}{k}+\frac{m}{k} = \frac{n+m}{k}\)
那么上下就会恰好抵消,那么我们把它看成多少都是无所谓的
因为分子分母总会消掉
如果 \(\frac{n}{k}+\frac{m}{k} < \frac{n+m}{k}\)
那么我们按 \(1\) 算答案就可能是错的
不过此时分子中含有的 \(p\) 的次数一定大于分母中含有 \(p\) 的次数
也就是说最终的答案和我们得到的答案都会是 \(0\)
所以把这个数看成多少都是无所谓的
注意特判 \(p=q\) 的情况
直接输出 \(1\) 就行了
因为此时只有 \(0\) 次幂会做贡献
代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define rg register
inline int read(){
rg int x=0,fh=1;
rg char ch=getchar();
while(ch<'0' || ch>'9'){
if(ch=='-') fh=-1;
ch=getchar();
}
while(ch>='0' && ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*fh;
}
const int maxn=2e5+5;
int mod,q,n,m,t,k=1,xs,jc[maxn],pre[maxn],ans;
inline int addmod(rg int now1,rg int now2){
return now1+=now2,now1>=mod?now1-mod:now1;
}
inline int delmod(rg int now1,rg int now2){
return now1-=now2,now1<0?now1+mod:now1;
}
inline int mulmod(rg long long now1,rg int now2){
return now1*=now2,now1>=mod?now1%mod:now1;
}
int ksm(rg int ds,rg int zs){
rg int nans=1;
while(zs){
if(zs&1) nans=mulmod(nans,ds);
ds=mulmod(ds,ds);
zs>>=1;
}
return nans;
}
int dfs(rg int now,rg int op){
xs+=op*now/mod;
if(now==0) return 1;
rg int tmp=mulmod(mulmod(ksm(jc[mod-1],now/mod),jc[now%mod]),dfs(now/mod,op));
return tmp;
}
int getf(rg int now,rg int op){
xs+=op*now/k;
rg int tmp=mulmod(mulmod(ksm(pre[k-1],now/k),pre[now%k]),dfs(now/k,op));
if(op==-1) tmp=ksm(tmp,mod-2);
return tmp;
}
int main(){
t=read(),q=read(),mod=read();
jc[0]=pre[0]=1;
if(q==mod){
while(t--){
n=read(),m=read();
printf("1\n");
}
return 0;
}
for(rg int r=q;r!=1;k++,r=mulmod(r,q));
for(rg int i=1;i<mod;++i) jc[i]=mulmod(jc[i-1],i);
for(rg int i=1,x=q;i<k;++i,x=mulmod(x,q)) pre[i]=mulmod(pre[i-1],x-1);
while(t--){
n=read(),m=read();
xs=0,ans=mulmod(mulmod(getf(n+m,1),getf(n,-1)),getf(m,-1));
if(xs) ans=0;
printf("%d\n",ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号