洛谷 AT2344 题解

题目传送门

---

题意：

给出两个长、宽分别为 $1$ 和 $w$ 的矩形，它们到原点的距离分别为 $a$ 和 $b$，将这两个矩形水平移动，合成一个长方形，求移动的最小距离。

---

思路：

根据题目所给出的图得知：

• 这两个矩阵的水平最短距离为：$b-(a+W)$。
  

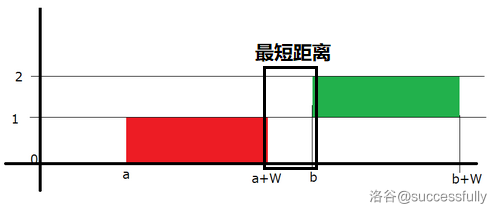
• 化简后得：$b-a-W$。

• 题目中并没有给定 $b$ 是大于 $a$ 的，而我们默认的是 $b>a$，所以在一开始就要判断 $a$ 和 $b$ 的大小关系。

• 最后要考虑特判，如果两个矩阵已经连接，答案就是 $0$。

---

code：

#include <bits/stdc++.h>
using namespace std;

long long w,a,b; 

int main(){
	cin>>w>>a>>b;
	if(a>b){
		swap(a,b);
	}
	int sum=b-a-w;
	if(sum<0)	sum=0;
	cout<<sum<<endl;
	return 0;
}