Solution Set 1

\(\text{「ABC222H」Beautiful Binary Tree}\)

\(\text{Link}\)

\(\text{Describe}\)

对于一个正整数 \(n\)，我们称满足以下条件的有根二叉树是一棵美丽的 \(n\) 阶二叉树。

• 每个节点有一个数字 \(0\) 或 \(1\)，节点 \(i\) 的数字记为 \(a_i\)。
• 每个叶子节点的数字定是 \(1\)。
• 可以通过进行如下的操作至多 \(n - 1\) 次，使得最终根节点上的数字为 \(n\)，其余节点的数字是 \(0\)。
  • 选择两个节点 \(u, v\)，其中 \(u\) 需要是 \(v\) 的父节点或父节点的父节点。作赋值 \(a_u\leftarrow a_u + a_v, a_v\leftarrow 0\)。

给定 \(n\)，请计算美丽的 \(n\) 阶二叉树的数量。答案对 \(998244353\) 取模。

\(\text{Solution}\)

容易发现美丽的 \(n\) 阶二叉树的等价限制为

• 每个叶子节点的数字是 \(1\)；

• 根的数字为 \(1\)；

• \(\forall (u,v)\in E,a_u=1\vee a_v=1\)；

考虑定义根的数字为 \(0/1\) 的 \(\text{GF}\) 记为 \(G/F\)，容易构造出 \(F,G\) 的关系

\[\begin{aligned} &F(x)=x(F(x)+G(x))^2+1\\ &G(x)=F^2(x)-1 \end{aligned} \]

转化为

\[F(x)=x(F^2(x)+F(x)-1)^2+1 \]

考虑用拉格朗日反演提取系数，因为右边的常数项无法与 \(x^k\) 消掉，考虑换元 \(H(x)=F(x)-1\)，有

\[\dfrac{H(x)}{(H^2(x)+3H(x)+1)^2}=x \]

其复合逆为 \(R(x)=\dfrac{x}{x^2+3x+1}\).

运用拉格朗日反演容易有

\[[x^n]H(x)=\dfrac{1}{n}[x^{n-1}](x^2+3x+1)^n \]

容易 \(\mathcal O(n)\) 直接计算。

\(\text{「CF566C」Logistical Questions}\)

\(\text{Link}\)

\(\text{Describe}\)

一棵 \(n\) 个节点的树，点有点权，边有边权。

两点间的距离定义为两点间边权和带权的 \(\frac 32\) 次方。

求这棵树的带权重心。

\(\text{Solution}\)

可以发现对于任何一个点计算带权距离和是 \(\mathcal O(n)\) 的，而且这个形式也不存在换根的可能性。考虑带权距离和的性质，下面记录 \(d(u,v)\) 为 \(u\) 到 \(v\) 路径的边权和。

\[F(u)=\sum_{v=1}^nw_vd^{\frac 32}(u,v) \]

考虑放在一条链 \((u,v)\) 上，考虑在靠近 \(u\) 的 \(\dfrac 1\lambda\) 分点

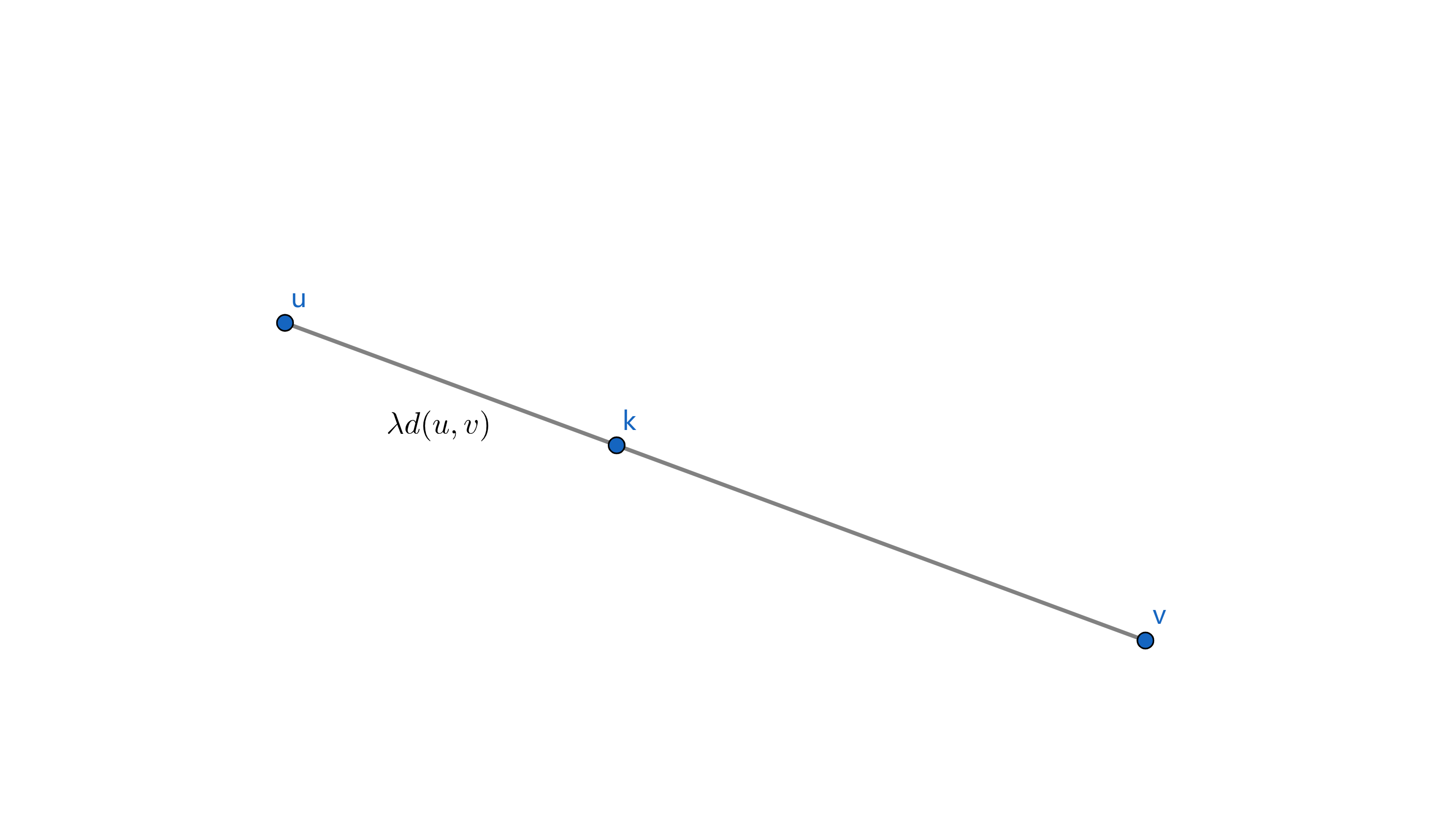
我们可以将 \(F(k)\) 看成随 \(\lambda\) 连续变化的函数 \(g(\lambda)\)，由于 \(x^{\frac 32}\) 为下凸函数，所以 \(g(\lambda)\) 也为下凸函数，下凸函数具有唯一最值点，如果最值点在点 \(u\) 上，\(u\) 就是带权重心，而最值点在边 \((u,v)\)，\(u/v\) 是带权重心，只需要 \(\mathcal O(n)\) 比较即可。

\(\text{「ABC318Ex」Count Strong Test Cases}\)