张宇基础三十讲补充知识点

张宇基础三十讲补充知识点

张宇三十讲中有些很基础的知识点缺少系统说明（也有可能是笔者自己听课看书不认真），很多问题不甚了了，自己上手就不知道某个公式到底能不能用。本文记录了笔者在学习过程中的一些疑惑，持续更新~

1. 什么时候可以替换等价无穷小

详细说明见这篇文章《彻底讲清楚等价无穷小使用规则》,简单总结一下：

1. 等价无穷小只是一种逼近而不相等；
2. 等价无穷小替换适用于乘除；
3. 某些情况下等价无穷小替换适用于加减是因为应用了极限运算的性质，例如：\(\lim \limits_{x\to0}\frac{\sin x-2x}{\tan x}=\lim \limits_{x\to0}\frac{x-2x}{x}=-1\)，其实际上是利用极限运算减法的性质分别计算了\(\frac{\sin x}{\tan x}\)和\(\frac{2x}{\tan x}\)的极限；
4. 泰勒展开是相等，可以直接替换；
5. 先通分再等价无穷小替换。

更新1：

今天在做极限时碰到了非常典型的一道题：求极限\(\lim\limits_{x\to0}(\frac{e^x+xe^x}{e^x-1}-\frac1x)\)，注意到\(e^x-1\)在分母的位置，我就直接将其代换为\(x\)，求得答案为2，但实际答案为3/2。这里的问题在于没有先通分再替换。

为什么要先通分才能替换呢，详细说明可以看这篇文章《“等价无穷小量的替换”的详析》,简单来说每次替换等价无穷小可以理解为给整个式子乘了一个值为1的极限，例如\(\lim\limits_{x\to0}\frac{(x+1)\sin x}{x}=\lim\limits_{x\to0}\frac{(x+1)\sin x}{x}\times\lim\limits_{x\to0}\frac{x}{\sin x}\)然后进行约分。回到上式。如果对\(e^x -1\)进行代换，实际上已经把这个极限拆成了两个极限之差，或者另一项\(1/x\)要同乘\(\frac{e^x -1}{x}\)。

2. 复合函数的极限的定义

武忠祥11月14日每日一题有一道考查复合函数极限定义的题目：

已知\(\lim_{x\to x_0}\varphi(x)=0\)，则下列结论正确的个数为：

A. \(\lim_{x\to x_0}\frac{\sin\varphi (x)}{\varphi(x)}=1\)

B. \(\lim_{x\to x_0}[1+\varphi(x)]^{\frac {1}{\varphi(x)}}=e\)

C. 当\(x\to x_0\)时，\(\sin(\varphi(x))\sim \varphi(x)\)

D. 若\(\lim_{u\to0}f(u)=A\)，则\(\lim_{x\to x_0}f[\varphi(x)]=A\)

乍一看似乎结论都是对的，但事实上上述四个结论全错。仔细分析这道题，会发现命题A和命题C二者等价，而命题ABC是命题D的加强命题，增加了“\(f(x)\)在\(u\)处连续这一个条件”。

解决这个问题，需要用到两个关于复合函数极限的定义和求解的定理：

定理一：

定理二：

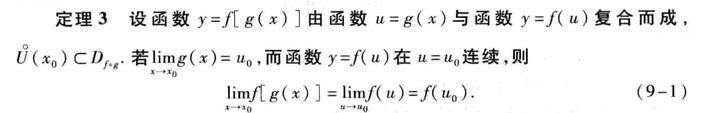
应用定理一，显然命题D不成立；应用定理二，则命题ABC不成立。严格来说，上述两个定理都是复合函数极限存在的充分条件，那为什么我们会说通过这两个定理就可以得到四个命题均不成立的结论呢。接下来我们聊聊这两个定理。

首先是定理一，其规定了复合函数的极限运算法则，注意这里的\(f(x)\)和\(g(x)\)是任意函数，定理里其它部分都很显然，唯独\(g(x)\neq u_0\)这个条件很突兀，为什么需要存在一个去心邻域\(\mathring{U}(x_0, \delta_0)\)使得\(g(x) \neq u_0\)。考虑如下一个反例：\(g(x)\)是常函数\(g(x)=C\)，而\(f(x)\)在\(C\)处有一个可去间断点，即\(f(x)\)在\(x=C\)处的极限值存在但不等于\(f(C)\)。在这种情况下，当求\(\lim_{x\to x_0}f[g(x)]\)时，\(x\)从两侧趋向\(x_0\)，\(u=g(x)=C\)为常数，从而\(\lim_{x\to x_0}f[g(x)]=f(C)\)，但是\(\lim_{x\to C}f(x)\neq f(C)\)，即若缺失“存在一个去心邻域\(\mathring{U}(x_0, \delta_0)\)使得\(g(x) \neq u_0\)”这一条件，无法推出复合函数的极限值等于\(\lim_{x\to x_0}f[g(x)]=\lim_{u\to u_0}f(u)=A\)。故而命题D错误。

审视上一过程，问题的关键在于\(f(x)\)在\(C\)处存在可去间断点。那如果其不存在间断点，也就是\(f(x)\)是连续函数呢？对于连续函数有函数值处处等于极限值，也就是\(\lim_{x\to x_0}f[g(x)]=\lim_{u\to u_0}f(u)=A\)。但别忘了还要保证这个极限在定义上存在，就是说\(f[g(x)]\)在\(x_0\)的去心邻域上有定义。原命题ABC中，都出现了\(1/\varphi(x)\)的形式，但并一定能保证找到一个领域使得\(\varphi(x) \neq 0\)，例如\(\varphi(x)=x\sin(x)\)在\(0\)附近找不到任何一个邻域使得\(x\sin(x) \neq 0\)恒成立，故而ABC错误。

本文参考了知乎上@马同学的文章，原文中使用动图说明，数形结合深入浅出，讲得很好！