中缀表达式转后缀表达式

中缀表达式转后缀表达式

一、中缀表达式和后缀表达式的区别

中缀表达式就是我们通常认知中的表达式，比如

\[1+((2+3)*4)-5 \]

这样的表达式虽然容易被人所理解，但是不容易被机器所识别，为此推出了 后缀表达式。

后缀表达式又被叫做 逆波兰表达式，逆波兰表达式 不需要被括号所识别 ，且容易被机器识别。

二、中缀表达式转后缀表达式的过程

我们随意的拟定一个中缀表达式，比如：

\[1+5*(3+2)-4*5 \]

我们对中缀表达式进行一步一步转换，转换方式如下：

1. 遇到操作数时直接加入集合

2. 遇到操作符，与栈顶操作符比较优先级:

   • 如果栈为空，或者 , 栈顶元素为’ \((\) ’，入栈
   • 如果优先级 \(>\) 栈顶操作符优先级，入栈
   • 如果优先级 \(<=\) 栈顶操作符优先级，弹出栈顶元素入集合，再次进行对比

3. 遇到括号时：

   • 如果为左括号，直接加入栈
   • 如果为右括号，依次弹出栈顶元素入集合，并且,再次对比，直到遇到左括号，弹出栈顶元素不入集合。

4、最后将栈顶元素依次弹出入集合

做从左向右扫描，转化过程如下：

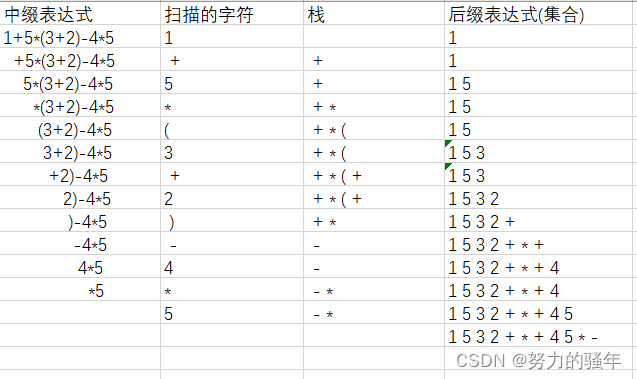
三、实现代码

#include <bits/stdc++.h>
using namespace std;

// 中缀表达式转后缀表达式
/*
测试用例1:
a+b*c+(d*e+f)*g

答案：
abc*+de*f+g*+


测试用例2：
(6+3*(7-4))-8/2

答案：
6 3 7 4 - * + 8 2 / -

测试用例3：
(24*(9+6/3-5)+4)
答案：
24 9 6 3 / + 5 - * 4 +

测试用例4:
2*3*2+5/3

*/

unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; // 操作符优化级
string t;                                                           // 结果串
stack<char> stk;                                                    // 栈
// 中缀转后缀
string infixToPostfix(string s) {
    for (int i = 0; i < s.size(); i++) {
        // ①数字
        if (isdigit(s[i])) {
            int x = 0;
            while (i < s.size() && isdigit(s[i])) {
                x = x * 10 + s[i] - '0';
                i++;
            }
            i--;
            t += to_string(x), t += ' ';
        } else if (isalpha(s[i])) // ②字符,比如a,b,c
            t += s[i], t += ' ';
        else if (s[i] == '(')          // ③左括号
            stk.push(s[i]);            // 左括号入栈
        else if (s[i] == ')') {        // ④右括号
            while (stk.top() != '(') { // 让栈中元素(也就是+-*/和左括号)一直出栈，直到匹配的左括号出栈
                t += stk.top(), t += ' ';
                stk.pop();
            }
            stk.pop(); // 左括号也需要出栈
        } else {
            // ⑤操作符 +-*/
            while (stk.size() && h[s[i]] <= h[stk.top()]) {
                t += stk.top(), t += ' ';
                stk.pop();
            }
            stk.push(s[i]); // 将自己入栈
        }
    }
    // 当栈不为空时，全部输出
    while (stk.size()) {
        t += stk.top(), t += ' ';
        stk.pop();
    }
    return t;
}

int main() {
    string infix = "(24*(9+6/3-5)+4)";
    string postfix = infixToPostfix(infix);
    cout << "中缀表达式: " << infix << endl;
    cout << "后缀表达式: " << postfix << endl;
    return 0;
}