【数据结构】二维树状数组
【数据结构】二维树状数组
一、二维树状数组
二维树状数组,其实就是一维的树状数组上的节点再套个树状数组,就变成了二维树状数组了。
const int N = 1e3 + 10;
int tr[N][N], n, m;
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
int query(int x, int y) {
int ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
二、单点修改,区间查询
给出一个 \(n × m\) 的零矩阵 \(A\) ,你需要完成如下操作:
- \(1\) \(x\) \(y\) \(k\) :表示元素 \(A\)_{\(x\) , \(y\)} 自增 \(k\)
- \(2\) \(a\) \(b\) \(c\) \(d\): 表示询问左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵内所有数的和

单点增加,因此可以直接加上就可以了
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5000; // 2^(12)=4096
int n, m;
LL tr[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int opt;
while (cin >> opt) {
if (opt == 1) {
int x, y, d;
cin >> x >> y >> d;
add(x, y, d);
} else {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
}
}
return 0;
}
三、区间修改,单点查询
给出一个 \(n × m\) 的零矩阵 \(A\) ,你需要完成如下操作:
- \(1 \, a \, b \, c \, d \, k\):表示左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵内所有数都自增加 \(k\);
- \(2 \, x \, y\) :表示询问元素 \(A_{x,y}\) 的值。
只需要利用一个二维树状数组,维护一个二维差分数组,单点查询即可。
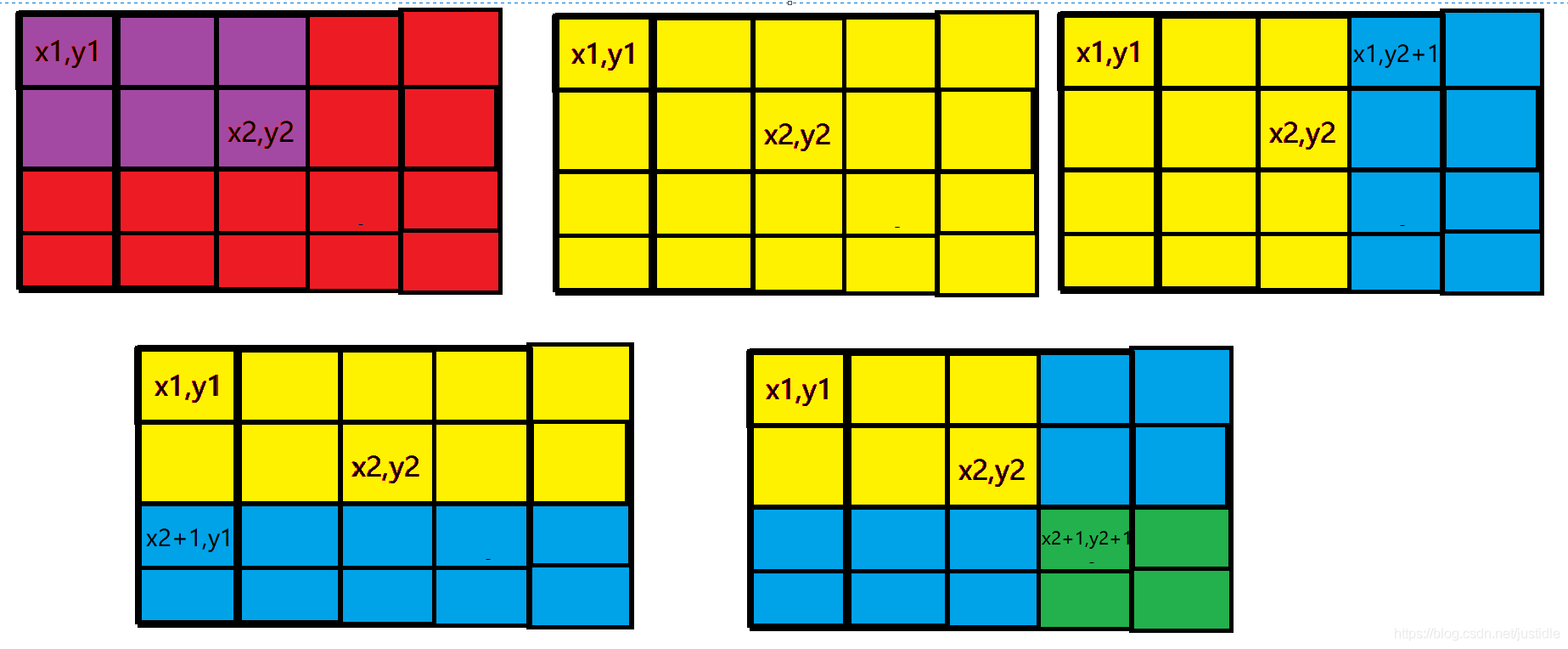
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5000;
int bit[N][N];
int n, m;
LL tr[N][N];
#define lowbit(x) (x & -x)
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j))
tr[i][j] += d;
}
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i; i -= lowbit(i))
for (int j = y; j; j -= lowbit(j))
ret += tr[i][j];
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int op;
while (cin >> op) {
if (op == 1) {
int x1, y1, x2, y2, d;
cin >> x1 >> y1 >> x2 >> y2 >> d;
//二维差分
add(x1, y1, d);
add(x1, y2 + 1, -d);
add(x2 + 1, y1, -d);
add(x2 + 1, y2 + 1, d);
} else {
int x, y;
cin >> x >> y;
cout << query(x, y) << '\n';
}
}
return 0;
}
四、区间修改,区间查询
给定一个大小为 \(N × M\) 的零矩阵,直到输入文件结束,你需要进行若干个操作,操作有两类:
-
\(1 \, a\, b\, c\, d\, x\),表示将左上角为 \((a,b)\) ,右下角为 \((c,d)\) 的子矩阵全部加上 \(x\);
-
\(2\, a\, b\, c\, d\,\) , 表示询问左上角为 \((a,b)\) ,右下角为 \((c,d)\) 为顶点的子矩阵的所有数字之和。
考虑前缀和 \(sum[i][j]\) 和 原数组 \(a\) , 差分数组 \(d\) 之间的关系。
首先\(\displaystyle sum[i][j]=\sum_{x=1}^i\sum_{y=1}^ja[x][y]\) (二维前缀和)
双由于\(\displaystyle a[x][y]=\sum_{u=1}^x\sum_{v=1}^yd[u][v]\) (差分数组与原数组关系)
所以:
可以说是非常复杂了......
统计\(d[u][v]\)出现次数
-
从\(a[1][1]\)到\(a[i][j],d[1][1]\)全都要出现一次,所以有\(i×j\)个\(d[1][1]\),即\(d[1][1]×i×j\)
-
从\(a[1][1]\)到\(a[i][j]\),\(d[1][2]\)出现了多少次呢?头脑中出现一个二维差分转原数组(本质就是一个原数组转二维前缀和)的图像:
- \(i=1,j=1\)时, \(d[1][2]\)就没有出现
- \(i=1,j=2\)时, \(d[1][2]\)出现\(1\)次
- ...
- \(i=2,j=1\)时, \(d[1][2]\)就没有出现
- \(i=2,j=2\)时, \(d[1][2]\)出现\(1\)次
- ...
总结一下:
- \(d[1][2]×i×(j−1)\)
- \(d[2][1]×(i−1)×j\)
- \(d[2][2]×(i−1)×(j−1)\)
等等……
所以我们不难把式子变成:
展开得到:
也就相当于把这个式子拆成了四个部分:
\(\displaystyle ① (i+1)(j+1)×\sum_{x=1}^i\sum_{y=1}^jd[x][y] \\
② −(j+1)×\sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅x) \\
③ −(i+1)×\sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅y) \\
④ \sum_{x=1}^i\sum_{y=1}^j(d[x][y]⋅xy)\)
所以我们需要在原来 \(C_1[i][j]\) 记录 \(d[i][j]\) 的基础上,再添加三个树状数组:
\(C_2[i][j]\) 记录 \(d[i][j]⋅i\)
\(C_3[i][j]\) 记录 \(d[i][j]⋅j\)
\(C_4[i][j\)] 记录 \(d[i][j]⋅ij\)
这样一来,就能通过数组\(a[i][j]\)的差分数组\(d[i][j]\)来得到\(a[i][j]\)的前缀和数组\(sum[i][j]\)。
最后,易知\((x_1,y_1)\)到\((x_2,y_2)\)的矩阵和就是一个标准的二维前缀和公式,等于$$\large sum[x_2][y_2]−sum[x_2][y_1−1]−sum[x_1−1][y_2]+sum[x_1−1][y_1−1]$$
代码模板
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2050;
int n, m;
LL C1[N][N], C2[N][N], C3[N][N], C4[N][N];
#define lowbit(x) (x & -x)
//维护四个树状数组
void add(int x, int y, int d) {
for (int i = x; i <= n; i += lowbit(i))
for (int j = y; j <= m; j += lowbit(j)) {
C1[i][j] += d;
C2[i][j] += d * x;
C3[i][j] += d * y;
C4[i][j] += d * x * y;
}
}
//查询左上角为(1,1)右下角为(x,y)的矩阵和
LL query(int x, int y) {
LL ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
for (int j = y; j > 0; j -= lowbit(j)) {
ret += (x + 1) * (y + 1) * C1[i][j];
ret -= (y + 1) * C2[i][j];
ret -= (x + 1) * C3[i][j];
ret += C4[i][j];
}
}
return ret;
}
int main() {
//加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
int op;
while (cin >> op) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
if (op == 1) {
int d;
cin >> d;
//维护四个数组
add(x1, y1, d);
add(x1, y2 + 1, -d);
add(x2 + 1, y1, -d);
add(x2 + 1, y2 + 1, d);
} else
cout << query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1) << '\n';
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号