AcWing 98. 分形之城

\(AcWing\) \(98\). 分形之城

参考题解

一、题目描述

城市的规划在城市建设中是个大问题。

不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。

而这座名为 \(Fractal\) 的城市设想了这样的一个规划方案，如下图所示：

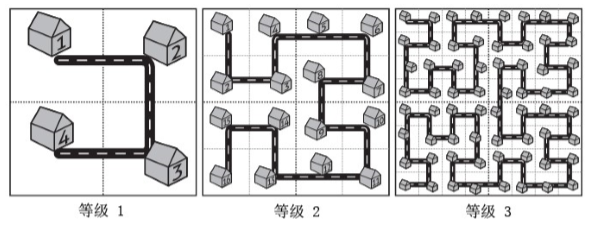
当城区规模扩大之后，\(Fractal\) 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。

对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。

虽然这个方案很烂，\(Fractal\) 规划部门的人员还是想知道，如果城市发展到了等级 \(N\)，编号为 \(A\) 和 \(B\) 的两个街区的 直线距离 是多少。

街区的距离指的是街区的 中心点之间的距离，每个街区都是边长为 \(10\) 米的正方形。

输入格式
第一行输入正整数 \(n\)，表示测试数据的数目。

以下 \(n\) 行，输入 \(n\) 组测试数据，每组一行。

每组数据包括三个整数 \(N,A,B\)，表示城市等级以及两个街区的编号，整数之间用空格隔开。

输出格式
一共输出 \(n\) 行数据，每行对应一组测试数据的输出结果，结果四舍五入到整数。

数据范围
\(1≤N≤31,1≤A,B≤2^{2N},1≤n≤1000\)

输入样例：

3 
1 1 2 
2 16 1 
3 4 33 

输出样例：

10 
30 

二、理解题意

本题看懂题目花费了大量的时间，后面理解题意如下：
等级一：\(4\)个点,等级二: \(16\)个点,等级三:\(64\)个点... 至于贯穿这些点的线，是城市编号增长的顺序。

分析从等级一如何到等级二,原来的城区设为\(A\):

• \(A\)顺时针旋转\(90\)度,再关于中间线翻转一下得到等级二的左上角城区
• \(A\)向右平移得到右上角的城区
• \(A\)向右平移再向下平移得到右下角的城区
• 至于左下角城区，一会再说。

三、数学知识

我们知道，两点之间距离的平方是对应横纵坐标距离之差的平方和。

欧几里得距离

坐标旋转公式：比如第一象限的点(\(1,2\))，顺时针旋转\(90\)度得到的点在第四象限，也就是(\(2，-1\))，逆时针旋转\(90\)度得到的点在第二象限，也就是(\(-2,1\))。更一般的，(\(x，y\))顺时针旋转\(90\)度得到(\(y，-x\))，逆时针得到 (\(-y，x\))。

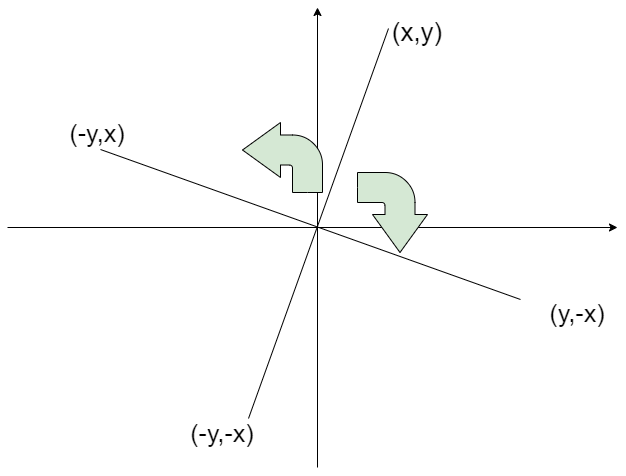
原坐标	顺时针90度	逆时针90度	180度
\((x,y)\)	\((y,-x)\)	\((-y,x)\)	\((-y,-x)\)

最重要的是确定坐标原点以及坐标系，大多数人都是按照二维数组的思想，把左上角第一个点作为原点，往下的方向作为\(x\)轴正方向，往右的方向作为\(y\)轴正方向，然后旋转都是绕左上角第一个点旋转，这样造成的问题就是左下角的城区在计算坐标时，逆时针旋转会转偏了，不容易计算。

个人浅见是按照各个等级城区中心为坐标原点:

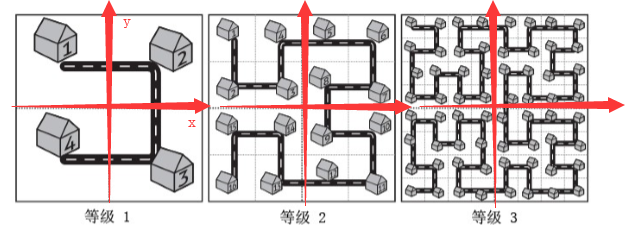
刚开始一直是以城区一的中心为原点，然后图一的四个点坐标分别为：\((-1,1),(1,1),(1,-1),(-1,-1)\)

• 左上角：\((x,y)\)关于原点顺时针\(90\)度旋转得到\((y,-x)\)再关于\(y\)轴轴对称变换得到\((-y,-x)\)；
• 右上角：\((x,y)\)向右平移\(2*len\)个单位得到\((x+2*len,y)\)，注意这里的\(len\)在代码中有定义；
• 右下角：\((x,y)\)向右平移\(2*len\)个单位得到\((x+2*len，y)\)再向下平移\(2*len\)个单位得到\((x+2*len，y-2*len)\)；
• 左下角：\((x,y)\)逆时针旋转\(90\)度得到 \((-y,x)\)，再关于\(y\)轴轴对称变换得到\((y,x)\)，注意这里四个点的中心是旋转中心，所以只是换了方向，本质四个点还在原地，最后再 向下 平移\(2*len\)得到\((y，x-2*len)\).

以上是以第一行第一列的点为坐标原点(旋转中心)经坐标变换得到其他城区的点的，但是并不能\(ac\)，因为图一这样旋转变换得到图二没问题，但是图二绕原来的旋转中心再转就会转歪，后面坐标便不对了。解决办法就是一轮坐标变换后便改变坐标原点(旋转中心)，比如等级一经坐标变换后得到等级二的四个坐标后，立刻调整坐标原点(旋转中心)为等级二的中心，再推出等级三坐标，继续调整坐标原点，以此类推。

上面的调整坐标原点是向右下角移动，具体操作为调整原来的坐标，横坐标减小\(len\)，纵坐标增加\(len\)，也就是在上面推出的坐标后面对横纵坐标再次变换，注意必须先坐标转换再移动坐标原点，即得到:

• 左上角：\((-y，-x)\)改变坐标得到\((-y-len，-x+len)\)；
• 右上角：\((x+2*len，y)\)变成\((x+len，y+len)\)；
• 右下角：\((x+2*len，y-2*len)\)变成 \((x+len，y-len)\)；
• 左下角：\((y，x-2*len)\)变成\((y-len，x-len)\).

注意点：
1.代码中坐标公式是两步得到，第一步旋转平移，第二步移动原点。
2.虽然主体代码和\(yxc\)大佬一样，但是输出时是乘以\(5\)，看上面我写的关于等级一的四个坐标便可理解，原点不同。

\(Q\):有点不理解为啥需要\(10/2=5\)啊？
答：你认真看一下上面的第\(2\)张图，原来\(1\)，\(2\)小房子中间的距离是\(len=10\),现在，我们硬生生在它俩中间放上了原点，就相当于把原来的图给 细化了一倍 ,原来的坐标(指以左上角为坐标原点时)\((0,0)\),\((0,1)\)给变成了\((-1,1)\),\((1,1)\),那么边长变可以理解为缩短了一半\(len=10/2=5\)

四、实现代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
struct Node {
    LL x, y;
};

// 功能：获取等级为n,编号为m的街区坐标,比如13号街区，就是小房子的编号
Node dfs(LL n, LL m) {
    if (n == 0) return {0, 0}; // 递归出口
    LL len = 1LL << (n - 1);   // 当前等级的移动的距离

    LL cnt = 1LL << 2 * n; // 等级为n时，共多少个街区
    cnt /= 4;              // 前一等级的街区数量，同时也是四分之一街区数量

    // m % cnt,m街区在上一个等级中的街区编号
    Node pos = dfs(n - 1, m % cnt); // 递归获取到上一个等级的坐标

    LL x = pos.x, y = pos.y;
    LL z = m / cnt;                          // 城区的哪个角:左上，右上，右下，左下
    if (z == 0) return {-y - len, -x + len}; // 左上角，从上一个等级的坐标变换到当前等级的坐标
    if (z == 1) return {x + len, y + len};   // 右上角
    if (z == 2) return {x + len, y - len};   // 右下角
    return {y - len, x - len};               // 左下角
}

void solve() {
    LL n, a, b; // 在一个等级为n的城市中，计算街区a,b的欧几里得距离
    cin >> n >> a >> b;

    Node p1 = dfs(n, a - 1); // 计算街区a的坐标
    Node p2 = dfs(n, b - 1); // 计算街区b的坐标
    // Q:为什么要减1?
    // A:因为街区编号是从1开始的，我们在dfs计算过程中用到了取模，希望街区编号从0开始，这里做了一下减1变换

    double x = p1.x - p2.x;
    double y = p1.y - p2.y;
    printf("%.0lf\n", sqrt(x * x + y * y) * 5);
    // Q:为什么是5，而不是10？
    // A:这是因为坐标变换的原因，我们生生的在两个相邻的坐标间插入了一个中间值，相当于把坐标放大了一倍，最后乘系数时就需要减少1半
}

int main() {
    int T;
    cin >> T;
    while (T--) solve();
    return 0;
}