AcWing 217. 绿豆蛙的归宿

\(AcWing\) \(217\). 绿豆蛙的归宿

一、题目描述

给出一个有向无环的连通图，起点为 \(1\) ，终点为 \(N\)，每条边都有一个长度。

数据保证从起点出发能够到达图中所有的点，图中所有的点也都能够到达终点。

绿豆蛙从起点出发，走向终点。

到达每一个顶点时，如果有 \(K\) 条离开该点的道路，绿豆蛙可以选择任意一条道路离开该点，并且走向每条路的概率为 \(1/K\)。

现在绿豆蛙想知道，从起点走到终点所经过的路径总长度的 期望 是多少？

输入格式
第一行: 两个整数 \(N，M\)，代表图中有 \(N\) 个点、\(M\) 条边。

第二行到第 \(1+M\) 行: 每行 \(3\) 个整数 \(a,b,c\)，代表从 \(a\) 到 \(b\) 有一条长度为 \(c\) 的有向边。

输出格式
输出从起点到终点路径总长度的 期望值，结果四舍五入保留两位小数。

数据范围
\(1≤N≤10^5,1≤M≤2N\)

输入样例：

4 4
1 2 1
1 3 2
2 3 3
3 4 4

输出样例：

7.00

二、数学期望

视频讲解　数学期望及性质

参考题解

首先明白一点：到达某个结果的期望值 = 这个结果 * 从起始状态到这个状态的概率

\(Q:\)什么意思呢？

如图：

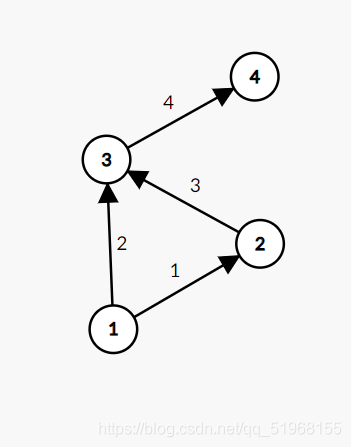
我们计算从\(1\)号点到\(3\)号点的期望距离

路径\(1\). \(\displaystyle 1−>3:E_1=2×\frac{1}{2}=1\)

路径\(2\). \(\displaystyle 1−>2−>3:E_2=1×\frac{1}{2}+3×\frac{1}{2}×1=2\)

这里路径\(2\)中从\(1\)到\(2\)概率为\(\displaystyle \frac{1}{2}\),但单看从\(2\)到\(3\)概率就是\(1\)，但是从\(1\)到\(3\)那就是从(\(1\)到\(2\)的概率)\(\displaystyle \frac{1}{2}\)×\(1\)(\(2\)到\(3\)的概率)=\(\displaystyle \frac{1}{2}\)。

所以从 点\(1\) 到 点\(3\) 的数学期望值=\(1+2=3\)

总结：概率是叠乘的

本题有 正推 和 倒推 两种写法:

二、正推法

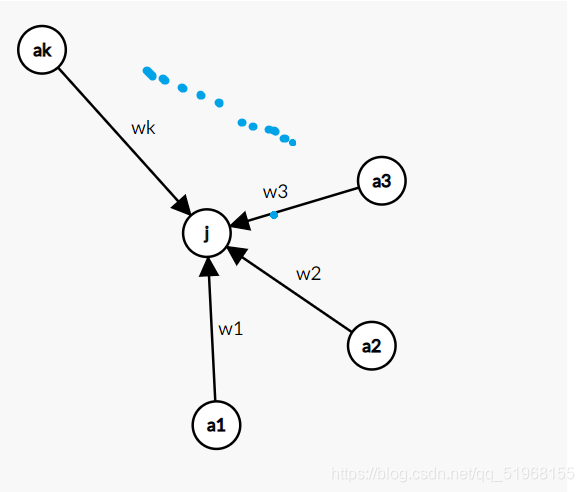
设：

• \(a_1, a_2, a_3 … a_k\) 到 \(j\) 的权值为 \(w_1, w_2, w_3 … w_k\),
• 从起点到这\(k\)个点的概率为：\(p_1, p_2, p_3 … p_k\)
• 每个点的出度为：\(out_1, out_2, out_3, … , out_k\)

这里的\(1\sim k\)个点的从起点的到该点的概率一定是确定的,也就是说这个点的概率是被更新完的，即此时这个点的入度为\(0\)！

那么就有：

\[f(i):表示从起点到i点的期望距离 \]

\[f(j)=\frac{f(1)+w_1\times p_1}{out_1}+\frac{f(2)+w_2\times p_2}{out_2}+\frac{f(3)+w_3\times p_3}{out_3}+...+\frac{f(k)+w_k\times p_k}{out_k} \]

正推代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;

//邻接表
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int n, m; // n个顶点，m条边

int out[N], in[N]; //出度,入度
double f[N], g[N]; // f:数学期望结果 g:概率

void topsort() {
    queue<int> q;
    //起点为1,起点的概率为100%
    q.push(1);
    g[1] = 1.0;
    f[1] = 0.0;

    // DAG，执行拓扑序,以保证计算的顺序正确，确保递归过程中，前序数据都已处理完毕
    while (q.size()) {
        auto u = q.front();
        q.pop();

        for (int i = h[u]; ~i; i = ne[i]) { //枚举的是每边相邻边
            int j = e[i];                   //此边，一端是t，另一端是j
            //此边边条w[i]
            f[j] += (f[u] + w[i] * g[u]) / out[u];
            g[j] += g[u] / out[u]; // p[j]也需要概率累加
            //拓扑序的标准套路
            in[j]--;
            if (!in[j]) q.push(j);
        }
    }
}

int main() {
    //初始化邻接表
    memset(h, -1, sizeof h);
    cin >> n >> m;

    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        //维护出度，入度
        out[a]++, in[b]++;
    }
    //拓扑序
    topsort();

    //正向递推，输出结果，保留两位小数
    printf("%.2lf", f[n]);

    return 0;
}

三、倒推法

现在学会了正推，来看看 逆推，即 从终点找到起点

设 \(f[x]\) 表示结点 \(x\) 走到终点所经过的路径的期望长度。显然 \(f[n]=0\) ，最后要求 \(f[1]\) 。

一般来说，初始状态确定时可用顺推，终止状态确定时可用逆推。

设 \(x\) 出发有 \(k\) 条边，分别到达 \(y_1,y_2...y_k\) ，边长分别为 \(z_1,z_2...z_k\) ，根据数学期望的定义和性质，有：

\[f[x]=\frac 1 k\times (f[y_1]+z_1)+\frac 1 k\times (f[y_2]+z_2)+...+\frac 1 k\times (f[y_k]+z_k)=\frac 1 k \times \sum_{i=1}^k(f[y_i]+z_i) \]

根据设定已经确定是能够到达 \(n\) 点了，概率为 \(1\) 。

\(f[n]\) 已知，需要求解 \(f[1]\) ，建立 反向图，按照 拓扑序 求解。

倒推代码

#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = N << 1;
int n, m;
int in[N], g[N]; //入度，入度的备份数组，原因：in在topsort中会不断变小受破坏

double f[N];

//链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

void topsort() {
    queue<int> q;
    q.push(n);
    f[n] = 0; // n到n的距离期望是0
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = h[u]; ~i; i = ne[i]) { //枚举每条入边(因为是反向图)
            int j = e[i];
            f[j] += (f[u] + w[i]) / g[j];
            in[j]--;
            if (in[j] == 0) q.push(j);
        }
    }
}
int main() {
    memset(h, -1, sizeof(h));
    cin >> n >> m;

    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(b, a, c); //反向图,计算从n到1
        in[a]++;      //入度
        g[a] = in[a]; //入度数量
    }
    topsort();
    printf("%.2lf\n", f[1]);
    return 0;
}