AcWing 255. 第K小数-------主席树(可持久化线段树) 模板题
\(AcWing\) \(255\). 第\(K\)小数
一、题目大意
给定长度为 \(N\) 的整数序列 \(A\),下标为 \(1\)∼\(N\)
现在要执行 \(M\) 次操作,其中第 \(i\) 次操作为给出三个整数 \(l_i,r_i,k_i\),求 \(A[l_i],A[l_{i+1}],…,A[r_i]\) (即 \(A\) 的下标区间 \([l_i,r_i]\))中第\(k_i\) 小的数是多少
输入格式
第一行包含两个整数 \(N\) 和 \(M\)
第二行包含 \(N\) 个整数,表示整数序列\(A\)
接下来 \(M\) 行,每行包含三个整数 \(l_i,r_i,k_i\),描述第 \(i\) 次操作
输出格式
对于每次操作输出一个结果,表示在该次操作中,第 \(k\) 小的数的数值
每个结果占一行
数据范围
\(N≤10^5,M≤10^4,|A[i]|≤10^9\)
输入样例:
7 3
1 5 2 6 3 7 4
2 5 3
4 4 1
1 7 3
输出样例:
5
6
3
二、解题思路
主席树
据说主席树是一个叫 黄嘉泰 的人发明的,与我朝某位胡主席拼音简写同名,简写\(hjt\),所以叫主席树。
一列数,可以对于每个点\(i\)都建一棵权值线段树,维护\(1\sim i\)这些数,每个不同的数出现的个数(权值线段树以值域作为区间)
现在,\(n\)棵线段树就建出来了,第\(i\)棵线段树代表\(1\sim i\)这个区间
例如,一列数,\(n\)为\(6\),数分别为1 3 2 3 6 1
首先,每棵树都是这样的:

以第\(4\)棵线段树为例,\(1\sim 4\)的数分别为1 3 2 3

因为是同一个问题,\(n\)棵权值线段树的形状是一模一样的,只有节点的权值不一样
所以这样的两棵线段树之间是可以相加减的(两颗线段树相减就是每个节点对应相减)
想想,第\(x\)棵线段树减去第\(y\)棵线段树会发生什么?
第\(x\)棵线段树代表的区间是\([1,x]\)
第\(y\)棵线段树代表的区间是\([1,y]\)
两棵线段树一减
设\(x>y,[1,x]−[1,y] = [y+1,x]\)
所以这两棵线段树相减可以产生一个新的区间对应的线段树!
等等,这不是 前缀和的思想 吗?
这样一来,任意一个区间的线段树,都可以由我这\(n\)个基础区间表示出来了!
因为每个区间都有一个线段树
然后询问对应区间,在区间对应的线段树中查找\(kth\)就行了
这就是主席树的一个核心思想:前缀和思想
具体做法待会儿再讲,现在还有一个严峻的问题,就是\(n\)棵线段树空间太大了!
如何优化空间,就是主席树另一个核心思想
我们发现这\(n\)棵线段树中,有很多重复的点,这些重复的点浪费了大部分的空间,所以考虑如何去掉这些冗余点
在建树中优化
假设现在有一棵线段树,序列往右移一位,建一棵新的线段树
对于一个儿子的值域区间,如果权值有变化,那么新建一个节点,否则,连到原来的那个节点上
- 下面用加入一段序列来进行举例:序列\(4\) \(3\) \(2\) \(3\) \(6\) \(1\)
区间\([1,1]\)的线段树(蓝色节点为新节点)

当我们插入一个元素的时候,我们其实只需要修改其中一条链的数据,对于其他剩余的节点我们就直接复制,同时复制旧版本的节点到新的树上,复制完后新版本的节点加上新的版本号。
下面的执行步骤同理
区间\([1,2]\)的线段树(橙色节点为新节点)
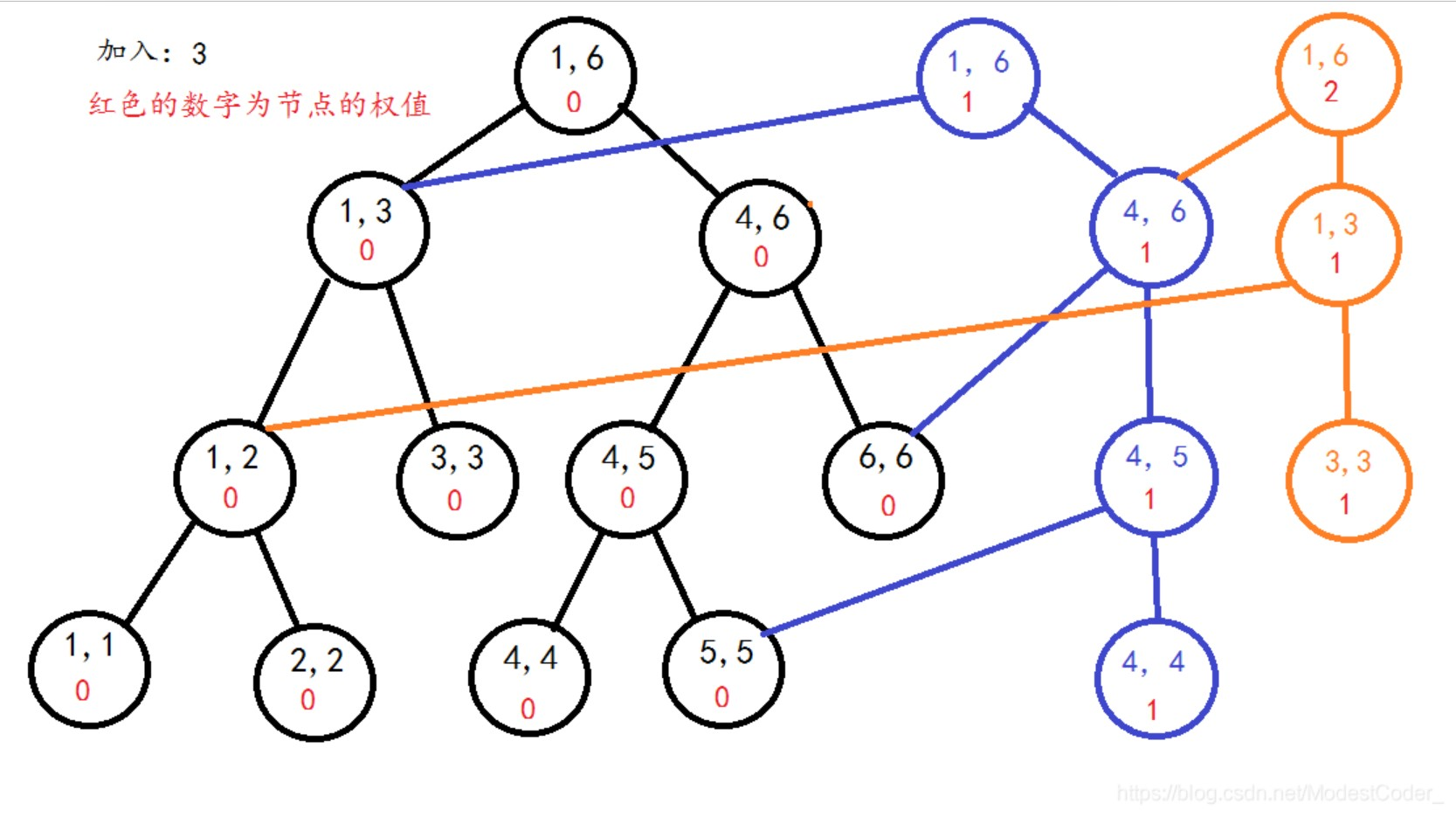
区间\([1,3]\)的线段树(紫色节点为新节点)
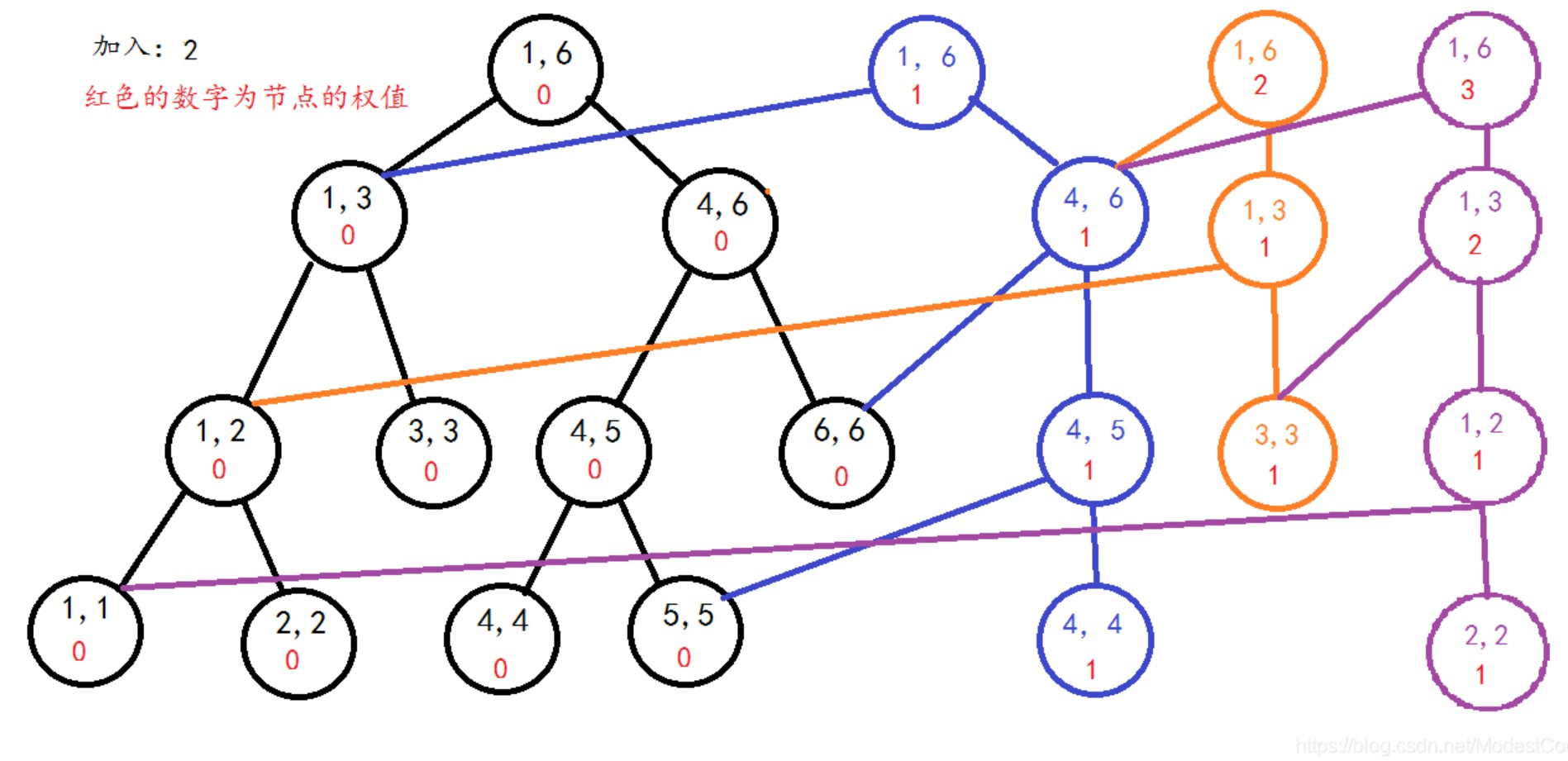
这样是不是非常优秀啊?
主席树的思想就讲到这里,接下来具体的代码来实现它
由于主席树需要不停地开新节点,所以用完全二叉树的方式来存就没有必要了,因为除了一开始建的树以外,之后的版本里节点的左右孩子的下标都是不固定的。所以我们采用存指针的方式(即存两个孩子在数组中的下标),而对于当前节点维护的区间范围,可以作为参数在调用函数的时候传进来。
三、本题思路
首先要查找的是 某个下标区间里 的第\(k\)小数。回想一下平衡树里查找第\(k\)小数的过程,如果每个节点维护子树节点数,并且维护当前区间内数字出现次数,那么就可以通过类似折半查找的做法把第\(k\)小的数求出来。
本题也类似,可以建立一个线段树,每个节点维护的是\(A\)在该范围内的数的个数。例如线段树里维护\([0,2]\)的区间的节点,记录的就是\(A\)中取值在\([0,2]\)有多少个数。一开始版本\(0\)的线段树相当于在维护空数组,接着将\(A[i]\)逐次插入,形成\(n\)个版本。第\(i\)个版本维护的就是\(A[1∼i]\)在各个区间里取值的数的个数。如果要查询在\(A[1]:A[r]\)内的第\(k\)小的数,就可以查看第\(r\)个版本的线段树,然后每次看一下左孩子维护的区间里有多少个数,如果有\(cnt\)个,并且\(k ≤ cnt\),那么就说明第\(k\)小的数在左半区间,则去左半区间找第\(k\)小的数;否则说明第\(k\)小的数在右半区间,则去右半区间找第\(k − cnt\)小的数。这和平衡树里求第\(k\)小的数的过程完全一样,也是在二分答案。
但是现在是要查询\(A[l:r]\)内第\(k\)小。这可以利用前缀和思想,我们考虑第\(r\)个版本和第\(l − 1\)个版本,两个版本的线段树的差,比如说比较两个版本维护区间\([a,b]\)的节点里记录的\(c\)值,分别叫\(c_r\) 和\(c_{l-1}\),那么\(c_r-c_{l-1}\)其实就是\(A[1:r]\)相比于\(A[1:l−1]\)而言,在\([a,b]\)里的数字个数多了多少个,那其实就是\(A[l:r]\)里有多少个数在\([a,b]\)里。有了这个信息,就可以二分答案来解决了。本题由于\(A[i]\)的取值范围过大,按照这个取值范围建线段树太费空间,需要做 离散化,即将\(A\)映射到\(0 ∼ n − 1\),然后用线段树维护\(0 ∼ n− 1\)这个区间即可。求完之后再映射回来即可。
四、主席树关键代码讲解
- 1、插入。这里的插入等价于普通线段树的单点修改,例如说插入\(x\),对应的就是被维护数组的下标\(x\)的地方增加\(1\)(这里的\(x\)是离散化后的),只不过主席树会在每次插入的时候新开一个版本。
代码如下:
//经典的主席树插入
void insert(int &u, int l, int r, int x) {
tr[++idx] = tr[u]; //新开一个节点idx++,将新节点指向旧的tr[u]
tr[idx].cnt++; //新节点的cnt,因为多插入了一个数字,所以个数+1,这样处理的话,省去了pushup
u = idx; //因为是地址引用,需要回写u等于idx
if (l == r) return; //如果已经到了叶子节点,上面的操作就足够了,可以直接返回,否则需要继续向下递归
int mid = l + r >> 1;
if (x <= mid)
insert(tr[u].l, l, mid, x); //因为tr[u]进入本函数时,最先把旧的复制过来,所以tr[u].l也是上一个版本的左儿子节点
else
insert(tr[u].r, mid + 1, r, x);
}
- 2、在\(A[l:r]\)里查询第\(k\)小。这需要在第\(l − 1\)版本和第\(r\)版本同时向下折半查找,每次都计算左半区间的元素个数\(c\),然后和\(k\)比较,如果左半区间元素个数大于等于\(k\) ,则说明答案在左半区间,去左半区间找第\(k\)小;否则说明在右半区间。去右半区间找第\(k − c\)小。
代码如下:
// p:前面的版本,q:后面的版本,[l,r]:控制的范围
// k:要查找第k小的数字
int query(int p, int q, int l, int r, int k) {
if (l == r) return l;
int mid = l + r >> 1;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
if (k <= cnt)
return query(tr[p].l, tr[q].l, l, mid, k);
else
return query(tr[p].r, tr[q].r, mid + 1, r, k - cnt);
}
五、静态数组离散化代码
#include <cstdio>
#include <algorithm>
using namespace std;
int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
const int N = 2e5 + 10;
int n, m;
int a[N], b[N], bl; // b和bl是一组,用于离散化的数组,bl为b的数组中有用数字的个数,一般下标0不放东西
struct Node {
int l, r, cnt;
} tr[N << 5];
int root[N], idx;
//用于离散化的二分查找
int find(int x) {
return lower_bound(b + 1, b + 1 + bl, x) - b;
}
//经典的主席树插入
void insert(int &u, int l, int r, int x) {
tr[++idx] = tr[u]; //新开一个节点idx++,将新节点指向旧的tr[u]
tr[idx].cnt++; //新节点的cnt,因为多插入了一个数字,所以个数+1,这样处理的话,省去了pushup
u = idx; //因为是地址引用,需要回写u等于idx
if (l == r) return; //如果已经到了叶子节点,上面的操作就足够了,可以直接返回,否则需要继续向下递归
int mid = l + r >> 1;
if (x <= mid)
insert(tr[u].l, l, mid, x); //因为tr[u]进入本函数时,最先把旧的复制过来,所以tr[u].l也是上一个版本的左儿子节点
else
insert(tr[u].r, mid + 1, r, x);
}
// p:前面的版本,q:后面的版本,[l,r]:控制的范围
// k:要查找第k小的数字
int query(int p, int q, int l, int r, int k) {
if (l == r) return l;
int mid = l + r >> 1;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
if (k <= cnt)
return query(tr[p].l, tr[q].l, l, mid, k);
else
return query(tr[p].r, tr[q].r, mid + 1, r, k - cnt);
}
int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
freopen("P3834.in", "r", stdin);
#endif
n = read(), m = read();
for (int i = 1; i <= n; i++)
a[i] = b[i] = read();
//数据范围太大,直接建线段树会MLE,但是比较稀疏,可以离散化后用相对应的序号,数据量就小了
sort(b + 1, b + 1 + n);
bl = unique(b + 1, b + 1 + n) - b - 1; //离散化后共m个数字
// 0号版本没有内容时,主席树是不需要进行build的,强行build时,可能会有部分测试点TLE
// 0号版本有内容时,主席树是需要build的,不build,初始值无法给上
// 主席树的数字增加,每增加一个,就相当于增加了一个版本root[i]记录了版本i的根节点
for (int i = 1; i <= n; i++) {
root[i] = root[i - 1]; //开新版本号i,抄袭上一个版本i-1的根节点
insert(root[i], 1, bl, find(a[i])); //向版本i中增加find(a[i])的值
}
while (m--) {
int l, r, k;
l = read(), r = read(), k = read();
//采用类似于前缀的方法,对位相减,由于是动态开点,需要指明控制范围[1,bl]
//要查询的数字是k
printf("%d\n", b[query(root[l - 1], root[r], 1, bl, k)]);
}
return 0;
}
六、\(vector\)离散化代码
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
//快读
int read() {
int x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
const int N = 2e5 + 10;
int n, m;
int a[N];
vector<int> ys;
struct Node {
int l, r, cnt;
} tr[N << 5];
int root[N], idx;
// 0号版本没有内容时,主席树是不需要进行build的,强行build时,可能会有部分测试点TLE
// 0号版本有内容时,主席树是需要build的,不build,初始值无法给上
int find(int x) {
return lower_bound(ys.begin(), ys.end(), x) - ys.begin();
}
//经典的主席树插入
void insert(int &u, int l, int r, int x) {
tr[++idx] = tr[u]; //新开一个节点idx++,将新节点指向旧的tr[u]
u = idx; //因为是引用,为了回传正确值,需要u=idx-1
tr[u].cnt++; //新节点的cnt,因为多插入了一个数字,所以个数+1,这样处理的话,省去了pushup
if (l == r) return; //如果已经到了叶子节点,上面的操作就足够了,可以直接返回,否则需要继续向下递归
int mid = l + r >> 1;
if (x <= mid)
insert(tr[u].l, l, mid, x); //因为tr[u]进入本函数时,最先把旧的复制过来,所以tr[u].l也是上一个版本的左儿子节点
else
insert(tr[u].r, mid + 1, r, x);
}
int query(int p, int q, int l, int r, int k) {
if (l == r) return l;
int mid = l + r >> 1;
int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;
if (k <= cnt)
return query(tr[p].l, tr[q].l, l, mid, k);
else
return query(tr[p].r, tr[q].r, mid + 1, r, k - cnt);
}
int main() {
//文件输入输出
#ifndef ONLINE_JUDGE
freopen("P3834.in", "r", stdin);
#endif
n = read(), m = read();
for (int i = 1; i <= n; i++) {
a[i] = read();
ys.push_back(a[i]);
}
//数据范围太大,直接建线段树会MLE,但是比较稀疏,可以离散化后用相对应的序号,数据量就小了
sort(ys.begin(), ys.end());
ys.erase(unique(ys.begin(), ys.end()), ys.end());
//主席树的数字增加,每增加一个,就相当于增加了一个版本root[i]记录了版本i的根节点
for (int i = 1; i <= n; i++) {
root[i] = root[i - 1];
insert(root[i], 0, ys.size() - 1, find(a[i]));
}
while (m--) {
int l, r, k;
l = read(), r = read(), k = read();
printf("%d\n", ys[query(root[l - 1], root[r], 0, ys.size() - 1, k)]);
}
return 0;
}
七、时间复杂度
时间复杂度\(O(nlogn+mlogn)\),即每次插入和查询时间复杂度都是\(O(logn)\),空间\(O(n+nlogn)\),每次插入都要新开\(O(logn)\)个节点。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号