K进制试题解析

一、先看一眼题

二、初步理解

很明显这是在将$10$进制数转为$k$进制数。从$0$开始，一直枚举到$n$，不断的向最后一位$+1$,直到末位为$k$，则设置本位为$0$,上位进$1$，当然，其它各位都要进行检查逐个上位~

三、问题逐个处理

判断题
1、 若$k=1$,则输出$ans$时，$len=n$。
作为第一个问题，难度肯定不能太高，一般采用特殊值法代入，尝试找出答案。我们以$k=1,n=3$代入 :

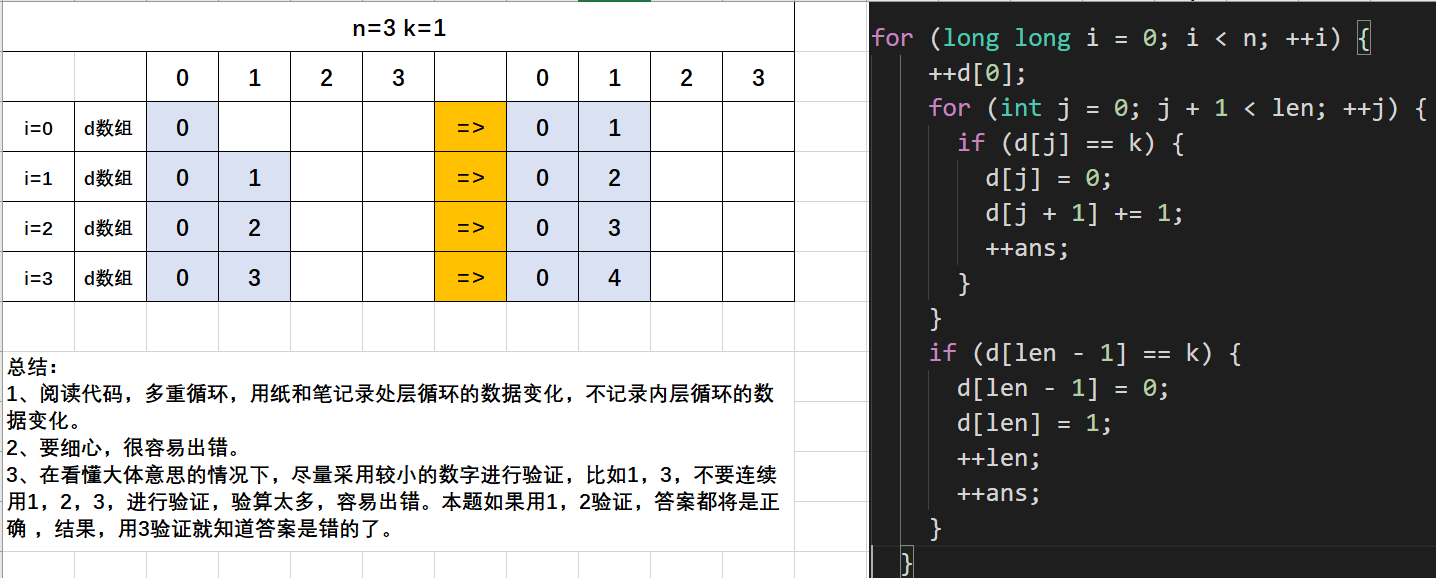
答案：$F$

2、若$k>1$,则输出$ans$时，$len$一定小于$n$。
意思就是说$k$进制的位数是否一定小于$n$。举一个比较常见的二进制例子：$2$的二进制是$10$,它的位数是$2$位，$len$($2$位)并一小于$n(2)$
答案：$F$

3、若$k>1$,则输出$ans$时，$k^{len}$一定大于$n$。
一个$k$进制数，如果有$len$位，每一位有$k$种变化，那么一共能表示$k^{len}$种数值，数值是从$0$到$k^{len}-1$的，所以说$k^{len}$一定大于$n$。
答案：$T$

4、若输入的$n$等于$10^{15}$,输入的$k$为$1$，则输出等于（$D$）
$A. 1$ $B. (10^{30}-10^{15})/2$ $C.(10^{30}+10^{15})/2$ $D.10^{15}$

解析：根据判断题1的举例，可以发现，当$k=1$时，若$i$会发生一次进位，共循环$n$次，因此共发生$n$次进位，即输出$n$。

5、若输入的$n$等于$205,891,132,094,649$,即$3^{30}$,输入的$k$为3，则输出等于（$B$）
$A.3^{30}$ $B.(3^{30}-1)/2$ $C. 3^{30}-1$ $D、(3^{30}+1)/2$
解析：本题是要求一共发生了多少次进位操作，如果十进制数是$100$,共发生了$100/10+100/100$次进位，即$n/10^1+n/10^2$次，同样$k=3$进制时，个位每$3$次都会进一位，因此$n$的个位会有$n/3$次进位。$n=3^{30}$时，共发生$3^{30}/3$+$3^{30}/3^2$+$3^{30}/3^3+...+3^0$,利用等比数列求和公式，所以答案是$B$

**6、若输入的$n$等于$100,010,002,000,090$，输入的$k$为$10$,则输出等于($B$)
$A、11，112，222，444，543$ $B、11，112，222，444，453$
$C、11，122，222，444，543$ $D、11，112，222，444，453$

解析：
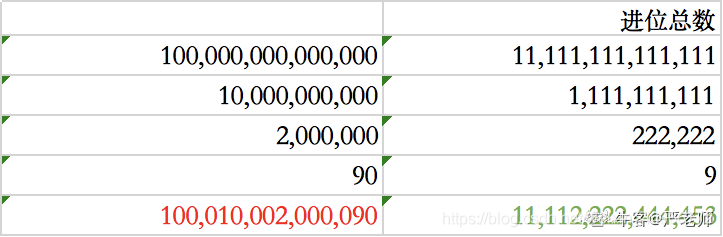
在前面第5题的分析基础上，本题也迎刃而解，$10$进制下，不用转换，$n$本身就是$10$进制展示的，将$100,010,002,000,090$依次拆分为下表格左边所示的$4$个数，参照第5题，求出每个数的进位总数，累加即可得到结果。