MX 练石 2025 NOIP #8

嘟错题了。嘟嘟嘟。

---

2025 --【炼石计划 NOIP】-- 第八套

链接：link
题解：link

时间：4h15min (2025.09.18 08:00~12:15)
题目数：4
难度：

A	B	C	D
\(\color{#FFC116} 黄\)	\(\color{#52C41A} 绿\)
*1300	*1900

估分：100 + 35 + 35 + 0 = 170
得分：100 + 35 + 30 + 0 = 165
Rank：26/151

---

场祭

读题。

A 好像很简单，贪心，证了一下发现对完了，写写写，欸怎么挂了，调了 20120712min 才发现不该偷懒只往 prque 里放一个 \(i\)，应该把 \(i,j\) 都放进去的，改了就过了。

B 好困难，不会，问题在于不会处理两棵子树中出现相同点的情况。不过好像可以拿 45pts 的暴力 + 特殊性质。先放一放去看 C。

C 瞎胡了一个 \(O(nm)\) dp，一写竟然是对的/oh

尝试优化，但是不会了。把 5pts 的全 a 串打了。还有 10pts 的线段树暴力修改的 \(O(\frac {nm} {|\Sigma|})\) 特殊性质，先放一放去写 B 的暴力吧。

B 想了个 \(O(n^2 2^n)\) 的暴力，写写写发现是 \(O(n^3 2^n)\) 的，写写写发现是 \(O(n^3 3^n)\) 的，知道为啥 \(n\) 只开 \(12\) 了，算了算大概 1e9，不过有个 \(\frac 1 2\) 的常数，而且还能剪点枝，问题不大，继续写。

写完发现没过样例，这时候才发现读错题了，\(l,r,k\) 是儿子个数而不是子树大小，不过也没时间去重新想正解了，改了改暴力过样例了。

去研究性质 A，但是这样例没道理啊，一条链不应该是只有一种情况吗？想不明白。

还剩 20min 去打 D 的暴力了。但是没时间了没调出来。

---

补题

补 B，几乎没做过图论计数导致的。令 \(f_{i,j,k}\) 为考虑前 \(i\) 个点，其中有 \(j\) 个点缺少父亲（即当前图是由 \(j\) 棵树构成的森林），缺少 \(k\) 个儿子的方案数。

说一下这个状态是怎么来的。因为限制一可以被拆成 \(0/1/2\) 三种独立情况的和，所以重点在于限制二。于是就有了第一维，这样保证了新加入的点一定大于图中任意一个点。

同时第三维也有了，毕竟需要确定到底需要几个儿子嘛。

但是这样就有一个问题，因为如果只有这两维，那就等价于钦定新加入的点一定会作为当前根的父亲 或者 某个节点的儿子了，但实际上它完全可以成为后面的点的儿子 且 不是当前根的祖先的，例如下面这棵树。所以就有了第二维。

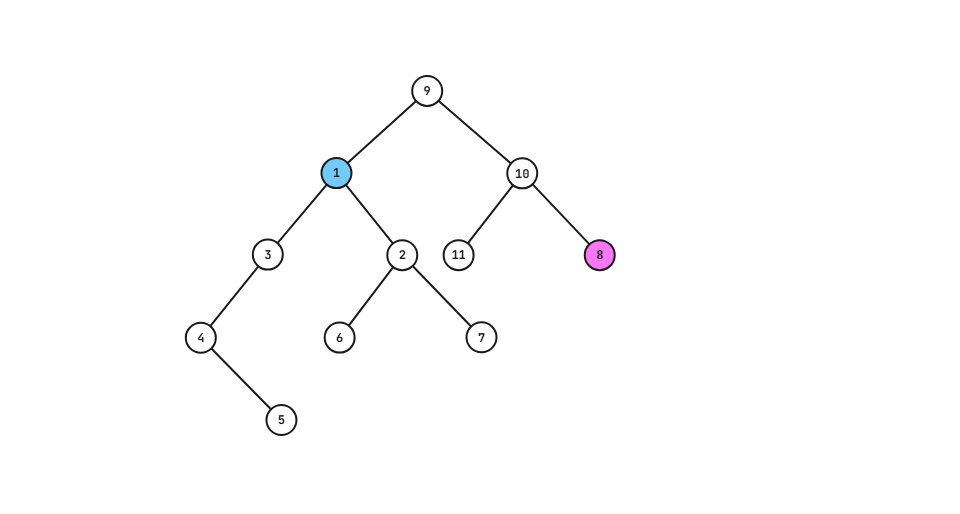
转移比较容易随便推推就有了。需要注意上面图中点 \(10\) 的情况，也就是把新加入的点接到一个缺父亲的点上面，并同时接到另一个缺儿子的点下面。

C 题解后面看不懂了。应该是注意到对于每个字符划分连续的区间，然后区间一块转移来着。

---

天依宝宝可爱！