MX 练石 2025 NOIP #1
啥啊。怎么打这么烂……
2025 --【炼石计划 NOIP】-- 第一套
时间:4.5h (2025.08.29 07:30~12:00)
题目数:4
难度:
| A | B | C | D |
|---|---|---|---|
| \(\color{#FFC116} 黄\) | \(\color{#52C41A} 绿\) | \(\color{#3498DB} 蓝\) | \(\color{#9D3DCF} 紫\) |
| *1300 | *1600 | *2100 | *? |
估分:[60,100] + 52 + 20 + 0 = [132,172]
得分:100 + 52 + 20 + 0 = 172
Rank:54/214
场祭
读题。
A 看上去挺简单的,开 A。但是发现直接二分每个数不可以,好像前缀处理也不怎么行。所以想到整体二分,但是这玩意其实以前根本没写过……
所以调了 20120712min,才两只 log 过去。不过两只 log 倒是跑不满,应该能卡过不少。
好像已经 2h40min+ 了,要寄了。
开 B,先把第一小问的 48pts 写了,然后去想正解,但是想不出来。
没时间了,写了 C 的 20pts 性质 A,摆了。
补题
草,A 脑抽了。
注意到有结论:「每次增加必须选择不同的元素」是没用的。因为限制的扩张速度只有 \(1\),所以「本次对 \(a_i\) 增加 \(2\),下次对 \(a_j\) 增加 \(2\)」与「本次对 \(a_i , a_j\) 分别增加 \(1\),下次分别增加 \(1\)」是等价的,晚一点增加不会导致被限制。
所以就只与需要增加的数量和有关了。
注意不能直接全算,因为本来就很大的元素有可能远远大于最终的 \(x\)。但是当 \(k \gets k+1\) 时,用到的元素一定会增加或不变,所以可以双指针维护,这样就只有一只 log 了(二分 \(x\))。
B 怎么也这么简单,考虑性质 C,即第一小问的答案为 \(0\)。显然贪心是成立的,每次跳到能跳到的最右边的 \(1\) 一定最优,这个显然可以倍增解决。
又发现当一段 \(0\) 必须跳的时候,无论起点在哪,经过 \(0\) 的次数都是一样的,所以可以直接把每一段长度为 \(x\) 的 \(0\) 缩成长度为 \(x \bmod k\) 的 \(0\),这样就可以用性质 C 的做法做了。
补 C,怎么也这么简单!显然是 dp,先考虑性质 B 怎么做,令 \(f_{i,j}\) 为第 \(i\) 步,一只手在 \(y_i\),另一只手在位置 \(j\) 的最小代价。可以发现每一步移动两只手一定不是更优的,所以只需要考虑移动哪只手到 \(y_i\) 即可。
- 移动 \(y_{i-1}\),即 \(y_{i-1} \to y_i , j \to j\)。所以枚举 \(j \in [1,n]\),转移 \(f_{i , j} \xleftarrow{\min} f_{i-1 , j} + d(y_i , y_{i-1})\)。
- 移动另一只手(令为 \(k\)),即 \(k \to y_i , j = y_{i-1}\)。所以枚举 \(k \in [1,n]\),转移 \(f_{i,y_{i-1}} \xleftarrow{\min} f_{i-1,k} + d(k,y_i)\)。
推广是容易的,如果出现了两个手都有要求的情况,直接分开,在转移第二只手的时候不允许第一种转移即可。
不过直接转移显然不可以,考虑数据结构优化。
先整理一下,可以得到:
注意到第二种转移就是区间加,线段树可以解决;第一种操作是单点修改,这个是容易的,但是还要求一个区间 min,而且 \(d(k,y_i)\) 不固定。
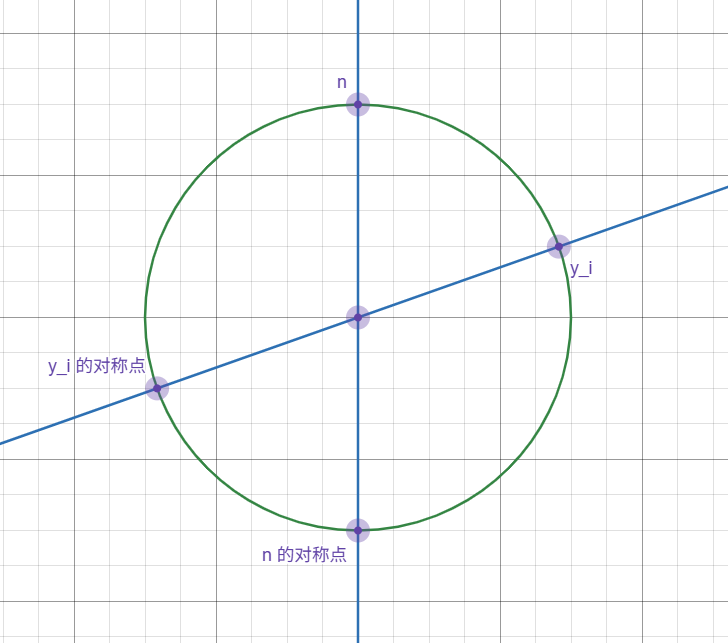
但是稍微注意一下,就可以发现 \(d(k,y_i)\) 一共只有四种可能,如图,考虑在一个圆上,\(y_i\) 和 \(y_i\) 的对称点 \(y_i + \frac n 2\) 是一对分界点,\(n\) 是一个分界点,再分讨 \(y_i\) 在圆的左半边还是右半边,最后只可能有 \(4\) 种取值,分别是 \(y_i-k , k-y_i , n-k+y_i , n-y_i+k\),所以只需要分别维护 \(f_{i,k} + k\) 和 \(f_{i,k} - k\) 的 min 即可,显然线段树可以解决。
D 是数位 dp,但是看上去好困难好困难。感觉这个是一天也补不出来的。
天依宝宝可爱!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号