字符串小记
相关性质
回文
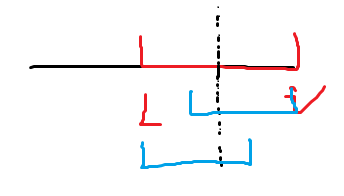
- 一个字符串的本质不同的回文子串只有 \(n\) 个。
- Proof: 考虑对于每个 \(i\),考虑他的最长后缀回文串 \([L, i]\)(红色串),然后一些别的回文后缀串(蓝色右串)。由于红色串是回文的,所以可以对称过去变成左边的串。所以蓝色串已经存在过了。
Border 与 周期
- 若字符串 \(s\) 存在长度为 \(x\) 的 \(\rm Border\),则存在长度为 \(n - x\) 的周期,反之亦然。
-
Proof:
考虑下面这个图
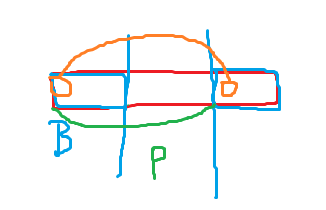
然后不难发现橙色部分都是一样的,于是 \(P\) 部分就是这个串的一个周期。
- 弱周期引理:若 \(p, q(p \neq q, p + q \le n)\) 都是字符串 \(s\) 的周期,则 \(\operatorname{gcd}(p, q)\) 也是周期。
-
Proof:
不妨令 \(p > q\),于是 \(d = p - q > 0\),若我们可以证明 \(d\) 也是周期,那么就可以通过辗转相除法证明 \(\operatorname{gcd}(p, q)\) 也是周期,于是考虑某个位置 \(i\) 与 \(i + d\) 的关系。
-
\(i \ge q:\) \(s_i = s_{i - q} = s_{i - q + p}\)
-
\(i \le n - p:\) \(s_i = s_{i + p} = s_{i + p - q}\)
于是可以证明 \(s_{i + d} = s_i\),即 \(d\) 也是串 \(s\) 的周期。然后由于 \(d \le p\),于是令 \(p' = d, q' = q\),重复做即可。
-
- 长度 \(\ge \lfloor \frac{n}{2} \rfloor\) 的 \(\rm Border\) 构成一个等差数列。
-
Proof: 首先转化成:长度 \(\le \lfloor \frac{n}{2} \rfloor\) 的周期构成一个等差数列。
接下来设最小的周期为 \(p\),然后长度 \(\le \lfloor \frac{n}{2} \rfloor\) 的另一个周期为 \(q\),由于弱周期引理, \(\operatorname{gcd}(p, q)\) 也是周期,于是 \(p | q\)。然后不难发现这显然构成了一个等差数列。
- 长度为 \(n\) 的字符串中的 \(\rm Border\) 的长度构成 \(O(\log n)\) 个等差数列。
- Proof: 每次把 \(\ge \lfloor \frac{n}{2} \rfloor\) 的 \(\rm Border\) 划分出去就划分成了一个子问题,于是递归 \(O(\log n)\) 层就结束了。
Manacher
先写回文相关的的东西。
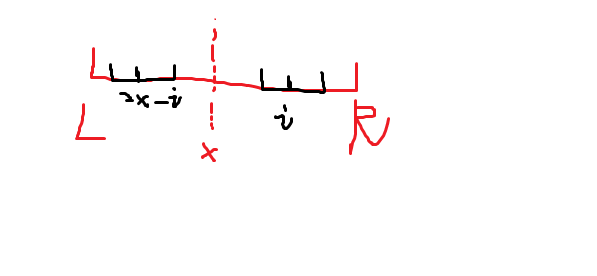
现在我们尝试求对于 \(1 \dots n\) 每个节点的最长回文半径 \(r_i\)。显然可以每次暴力拓展做到 \(O(n^2)\)。但是事实上,只需要一个剪枝就可以做到 \(O(n)\)。考虑最右边的回文串 \([L, R]\),以及回文中心 \(x\)。
-
假设 \(i > R\):直接暴力拓展即可。
-
否则:
我们可以考虑回文的一些性质,即利用之前已经计算过的信息,这是很多字符串算法优化时间复杂度的核心。于是把 \(i\) 对称到 \(i' = 2x - i\) 后,不难发现,左边的回文区间对称过来之后和右边是一样的,即 \([i' - r_{i'} + 1, i' + r_{i'} - 1]\) 区间放到 \(i\) 这个中心之后也是回文的,但是超过 \(R\) 的部分我们不知道,于是还得跟 \(R - i + 1\) 取 \(\min\) 即可。即初始化 \(r_i = \min(R - i + 1, r_{2x - i})\),然后暴力拓展。
每次更新一下 \([L, R]\) 即可。
然后考虑分析一下复杂度,由于 \(R\) 单调不降,于是时间复杂度显然也是 \(O(n)\)。然后假如要求奇回文串,在每一个字符中间加一个字符即可,然后字符为中心的回文串就是奇回文串。
qwq
#include<bits/stdc++.h>
#define ll long long
//#define int long long
#define pir pair<int, int>
#define pb emplace_back
using namespace std;
const int N = 2.2e7 + 10;
int n, m, R[N];
char s[N], t[N];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> (s + 1); n = strlen(s + 1); t[0] = '!'; t[++m] = '$';
for(int i = 1; i <= n; i++) t[++m] = s[i], t[++m] = '$';
t[++m] = '@'; int r = 0, c = 0, ans = 0;
for(int i = 1; i <= m; i++){
R[i] = (i > r) ? 1ll : min(R[2 * c - i], r - i + 1);
while(t[i + R[i]] == t[i - R[i]]) R[i]++;
if(i + R[i] - 1 > r) r = i + R[i] - 1, c = i;
ans = max(ans, R[i] - 1);
} cout << ans;
return 0;
}
PAM
现在我们想要求出对于 \(1 \dots n\),最长的回文后缀。即求出 \(\forall i, \max\{len_i | s[i - len_i + 1 \dots i] 为回文子串\}\)。
考虑构造一个自动机,每个节点代表着一个本质不同的回文串,然后转移边就是一个回文串两边加上两个字符。还有一个重要的元素就是 \(fail\) 指针,\(fail_u\) 表示节点 \(u\) 所代表的串的 最长回文后缀 所代表的节点。下面记节点 \(u\) 的字符 \(c\) 的出边节点为 \(trans_{u, c}\)。
但是这样有一个问题,假如只有一个根节点表示长度为 \(0\) 的节点,那么奇回文串就无法表示了。所以我们在加一个长度为 \(-1\) 的奇根,把长度为 \(0\) 的称作偶根。为了方便(在构造中有体现),令偶根的 \(\rm fail\) 指针为奇根。
接下来考虑使用 增量法 构造 \(\rm PAM\):
由于性质 \(1\),每次只需要加入最长的回文后缀。
设每次加入的字符是 \(s_i\),那么回文后缀要么是直接是 \(s_i\),或者是某个 \(i - 1\) 的回文后缀左边拼上 \(s_i\)。考虑 \(i - 1\) 最长回文后缀的节点 \(lst\),然后它的 \(fail_{lst}, fail_{fail_{lst}}\dots\) 构成的 \(\rm fail\) 链上面的节点构成了 \(i - 1\) 的所有回文后缀,把这个叫做 终止链。于是只要遍历一下终止链上面的节点即可。具体的,找到最长的一个满足左边的字符为 \(s_i\) 的回文后缀的节点 \(p\)。分类讨论一下:
-
\(trans_{u, c} \neq 0\):已经存在这个最长回文后缀,不需要考虑。
-
\(trans_{u, c} = 0\):那么新建一个节点 \(x\),然后更新一下 \(x\) 的信息,\(fail\) 指针直接在终止链上查一下次长的回文后缀即可,最后令 \(trans_{u, c} = x\)。
然后由于性质 \(1\),\(\rm PAM\) 的节点和转移边个数只有 \(O(n)\) 个,构造时相当于蜗牛爬杆,时间复杂度为 \(O(n)\)。
qwq
struct node{
int len, fail, cnt;
int son[26];
}tn[N];
int tot, n, lst;
il void init(){tot = 1; tn[1].len = -1; tn[0].fail = 1;}
il int getfail(int x){
while(s[n - tn[x].len - 1] != s[n]) x = tn[x].fail;
return x;
}
il void add(int sc){
s[++n] = sc; int p = getfail(lst);
if(!tn[p].son[sc]){
tn[++tot].len = tn[p].len + 2;
tn[tot].fail = tn[getfail(tn[p].fail)].son[sc];
tn[tot].cnt = tn[tn[tot].fail].cnt + 1; tn[p].son[sc] = tot;
} lst = tn[p].son[sc];
}
- 最小回文划分
然后考虑这个问题:
对于一个字符串 \(s\),考虑它的一个划分 \(t_1t_2\dots t_m\),其中 \(\forall 1 \le i \le m\),\(t_i\) 为回文串。求出满足条件的划分方案数。
考虑一个 \(O(n^2)\) \(\rm DP\):设 \(f_i\) 为 \(s[1 \dots i]\) 回文的方案数,则:
注意到每次都是找到每个位置的一些后缀回文串,于是考虑在 \(\rm PAM\) 上刻画这个过程同时通过回文的一些性质。注意到每个回文串若有一个回文后缀,那么那个回文后缀就是一个这个回文串的 \(\rm Border\)。于是假设考虑到位置 \(i\),那么以 \(i\) 为结尾的回文后缀可以构成 \(O(\log n)\) 个等差数列。那么假如对于每组回文串都可以快速更新并对 \(f_i\) 进行贡献,就可以每次快速求出 \(f_i\) 了。
令 \(dif_u = len_u - len_{fail_u}\),\(slink_u\) 为在 \(u\) 的 \(fail\) 链上最下面(深度最深)的节点 \(v\) 满足 \(dif_v \neq dif_u\)。
考虑令 \(g_u\) 为在 \(u\) 的 \(fail\) 链上 \(v \in [u \dots slink_u]\) 节点 \(f_{i' - len_v}\) 的和(\(i'\) 为上一次更新 \(g_u\) 时的位置)。那么每次更新完终止链上的 \(g_u\) 后,每次直接跳 \(slink\) 的节点,将这些 \(g\) 求和贡献到 \(f\) 即可。
于是接下来直接考虑如何更新 \(g\) 即可。直接爆算显然不行。考虑一些性质,画画图看看。
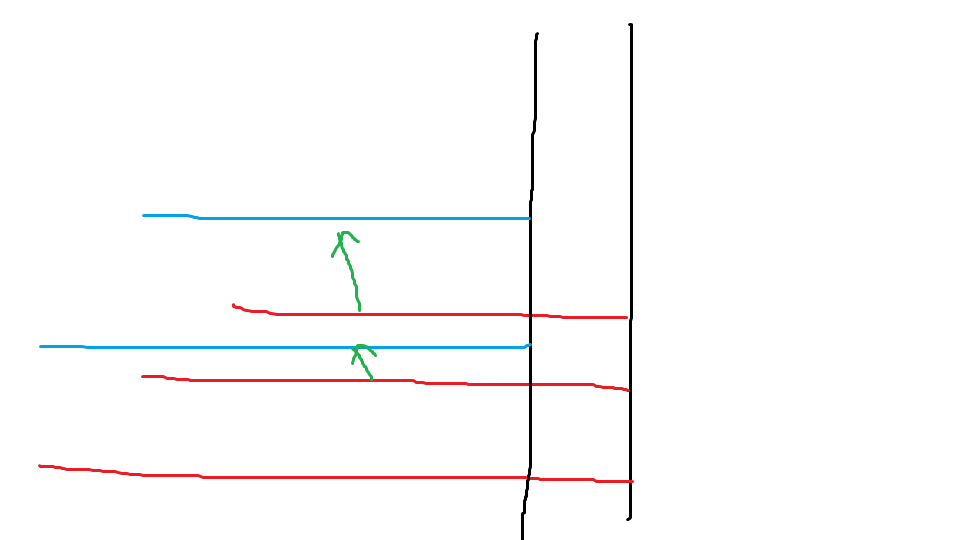
不难发现除了最短的串的贡献,其他已经包含到 \(g_u\) 里面了。然后最短的串长度显然就是 \(len_{slink_u} + dif_u\),这个更新是简单的。然后中间的 \(g\) 不用管就行,下次算的时候不会影响到什么。
Tips: 注意等差数列的定义上,最短的不会选入这个等差数列中,即 \(slink_u\) 虽然可以算入等差数列中,但是在 \(\rm PAM\) 中算作在下一个等差数列的最长的串。
于是时间复杂度就优化到了 \(O(n \log n)\)。
- 例题:CF932G
这个几乎就是板子,令 \(t = s_1s_ns_2s_{n-1}\dots s_{\frac{n}{2}}s_{n - \frac{n}{2} + 1}\),然后就相当于求串 \(t\) 的任意个偶回文划分。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10, S = 26;
const ll mod = 1e9 + 7;
int n;
ll f[N], g[N];
string str, str1;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
namespace PAM{
int n, tot, lst, slink[N], fail[N], len[N], son[N][S], dif[N];
int str[N];
void init(){tot = 1; fail[0] = 1; len[1] = -1; str[0] = -1;}
int getfail(int p){
while(str[n] != str[n - len[p] - 1]) p = fail[p];
return p;
}
void add(int c){
str[++n] = c; int p = getfail(lst);
if(!son[p][c]){
int cur = ++tot; len[cur] = len[p] + 2;
fail[cur] = son[getfail(fail[p])][c];
son[p][c] = cur; dif[cur] = len[cur] - len[fail[cur]];
if(dif[cur] != dif[fail[cur]]) slink[cur] = fail[cur];
else slink[cur] = slink[fail[cur]];
} lst = son[p][c];
}
};
using PAM::slink;
using PAM::lst;
using PAM::len;
using PAM::dif;
using PAM::fail;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
PAM::init();
cin >> str; n = str.size(); str = "*" + str;
str1.resize(n + 2);
for(int i = 1; i <= n / 2; i++) str1[2 * i - 1] = str[i], str1[2 * i] = str[n - i + 1];
//cerr << str1 << "\n";
f[0] = 1;
for(int i = 1; i <= n; i++){
PAM::add(str1[i] - 'a'); //cerr << "\nqwq " << i << "\n";
for(int p = lst; p > 1; p = slink[p]){
// cerr << len[p] << " " << fail[p] << "\n";
g[p] = f[i - len[slink[p]] - dif[p]];
if(slink[p] != fail[p]) ADD(g[p], g[fail[p]]);
if(i % 2 == 0) ADD(f[i], g[p]);
}
} cout << f[n];
return 0;
}
SAM
笔者学艺不精,很多证明都是一笔带过,若想要更严谨的博客可以看 Alex_Wei 老师的博客。
基础知识
接下来讲一下 \(\rm SAM\),这个东西还是非常强劲的。首先考虑一个可以 接受一个字符串 \(S\) 所有后缀 的 自动机。那么假设终止节点拓展到所有节点,根据定义,这个自动机就可以接受 \(S\) 的 所有子串 了!朴素的想,我们可以把他们全部塞进一个 \(\rm Trie\) 里面,但是这样的空间复杂度是 \(O(n^2)\) 的,显然不可接受。接下来考虑压缩一下状态,这个压缩后的自动机就被称作 \(\rm SAM\)。
我们希望 \(\rm SAM\) 是一个 \(\rm DAG\),因此定义他的转移 \(\delta(u, c)\) 为节点 \(u\) 所表示的 所有 串的末尾都加上字符 \(c\) 之后得到的状态,并要求一个 \(\delta(u, c)\) 只能唯一表示一个节点。并且我们希望一个子串 \(T\) 可以 唯一 对应到一个节点,但一个节点 不一定 唯一对应一个字符串。
定义一个 \(S\) 的子串 \(T\) 在 \(S\) 中出现的结尾位置集合为 \(\operatorname{endpos}(T)\),可以发现,若每个节点中表示的串的 \(\operatorname{endpos}\) 都一样的话,那么就可以完美的满足这个我们所需要的性质。即若令 \(\operatorname{substr}(u)\) 为节点 \(u\) 所表示的子串集合,于是 \(\exists G \in \{1, 2, \dots n\}\) 满足 \(\forall s \in \operatorname{substr}(u), \operatorname{endpos}(s) = G\)。然后接下来定义 \(\operatorname{endpos}(u) = G\)。也称这个节点所表示的字符串组成的集合为一个 endpos 等价类。
然后注意到一些性质:
- 对于一个 endpos 等价类,其长度集合构成一个区间,且较短的串是较长的串的后缀。
- 把图画出来理解一下就可以了。感性理解就是假如对于一个子串 \(T\),考虑他的一个后缀 \(\operatorname{suf}(T) = Y\),则 \(Y\) 在 \(S\) 中出现的概率更大,反之变小。
根据这个定理,就可以通过一个长度区间 \([\operatorname{minlen}(u), \operatorname{len}(u)]\) 描述一个节点中的子串。
对于 \(\rm SAM\) 上的两个不同的节点 \(u, v\),满足下面两个条件之间的其中恰好一个:
- \(\operatorname{endpos}(u) \subset \operatorname{endpos}(v)\)(也可能 \(u, v\) 反过来)
- \(\operatorname{endpos}(u) \cap \operatorname{endpos}(v) = \emptyset\)
且满足第一个条件的 \((u, v)\) 需要满足的充要条件为 \(\operatorname{substr}(v)\) 均为 \(\operatorname{substr}(u)\) 的后缀。
- 根据充要条件的话不难证明。
接下来就可以定义 \(fail_u\) 为节点 \(u\) 所表示最短后缀的最长真后缀(长度 -1)的节点所代表的节点。那么容易发现若 \(\forall i\) 连边 \((i, fail_i)\),就可以构成一棵树。我们令这个东西为 \(fail\) 树。
- 考虑一个节点 \(u\),令 \(anc(u)\) 为节点 \(u\) 在 \(fail\) 树上的祖先集合,则 \(\bigcup_{v \in anc(u)} \operatorname{substr(v)}\) 构成了长度为 \(1, 2\dots, \operatorname{len}(u)\) 且为 \(u\) 中最长的串的后缀。即 \(u\) 最长的串的 所有后缀。
- 根据性质 \(1\) 所解释的以及 \(fail\) 的定义,这些节点的 \([\operatorname{minlen}(v), \operatorname{len}(v)]\) 构成了一个连续的区间。这里也有一个结论:\(\operatorname{len}(fail_u) + 1 = \operatorname{minlen}(u)\)。
有了这些性质,就可以考虑如何对一个串构造 \(\rm SAM\) 了。
考虑增量法构造,即考虑构造出 \(S[1\dots n - 1]\) 的 \(\rm SAM\),再插入 \(c = S_n\),并更新相应的 \(\rm SAM\)。
首先类似 \(\rm PAM\) 的构造方法,维护一个可以描述结尾为 \(n - 1\) 的所有后缀的 终止链,其实就是 \(S[1\dots n - 1]\) 的构成的 \(fail\) 链。那么我们肯定要新建一个节点表示字符串 \(S[1\dots n]\),令这个节点为 \(cur\)。那么 \(\operatorname{endpos}(cur) = \{ n\}\)。于是我们还要考虑是否有另一些 在终止链上的 节点满足加上字符 \(c\) 后的 \(\operatorname{endpos}\) 集合只有 \(n\)。换句话说,也就是 \(\delta(p, c)\) 之前不存在,于是我们考虑在终止链上跳,若现在的节点 \(p\) 没有转移 \(\delta(p, c)\),就令 \(\delta(p, c) = p\)。若跳到了根节点,就说明 \(c\) 之前没有出现过,直接令 \(fail_{cur} = 0\) 即可。否则假设当前的 \(p\) 满足存在 \(q = \delta(p, c)\)。那么接下来需要分类讨论 \(len_p + 1\) 是否等于 \(len_q\)。(相当于 \(q\) 中的最长串是不是由 \(p\) 中的加上 \(c\) 而来)
- \(len_p + 1 = len_q\):此时 \(q\) 中的最长串恰好是 \(p\) 加上 \(c\) 得来的,此时 \(q\) 就是 \(S\) 最长的一个后缀满足 \(\operatorname{endpos}(q) \neq \operatorname{endpos}(cur)\)(因为 \(q\) 之前出现过,\(\operatorname{endpos}(cur) \subset \operatorname{endpos}(q)\))。于是恰好符合 \(fail_{cur}\) 的定义,于是令 \(fail_{cur}\) 即可。不理解可以看下面这个图:
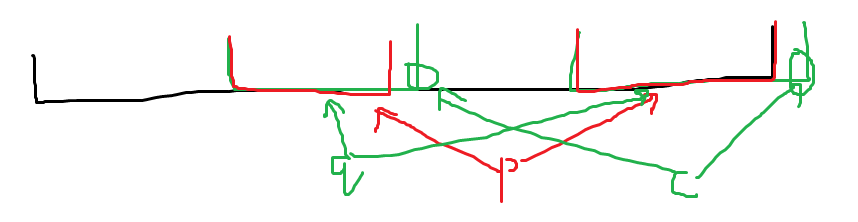
- \(len_p + 1 \ne len_q\),由于 \(len_p + 1 \le len_q\),于是 \(len_p + 1 < len_q\)。那么相当于还有别的状态 \(k\) 满足 \(len_k + 1 = len_p\),也就是 \(q\) 最长串并不是 \(p\) 的最长串加上 \(c\) 得到的。但是由于 \(p + c\) 这个串的 \(\operatorname{endpos}\) 集合增加了 \(n\)。于是需要分裂这两个串集合为两个不同的节点。具体的,我们新建一个状态 \(nq\) 表示 \(q\) 中长度 \(\le len_p + 1\) 的串,即令 \(len_{nq} = len_p + 1\),且原封不动的复制 \(q\) 的转移到 \(nq\),同时令 \(fail_q = nq\)。然后令 \(fail_p = nq\)。并且由于转移到 \(q\) 的节点可能不止一个,而我们的 \(nq\) 表示了 \(len \le len_p + 1\) 的 所有 后缀,我们需要把原来 \(len_o \le len_p\) 且满足 \(\delta(o, c) = q\) 的节点的 \(\delta(o, c)\) 赋值为 \(nq\)。但是注意到这个满足这个条件的串只有可能在 \(q\) 的 \(fail\) 链上的一个区间。于是再次更改即可。
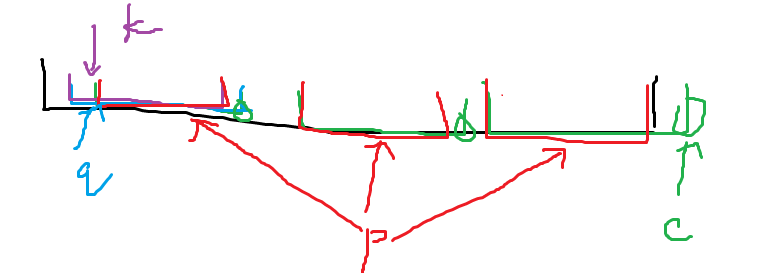
最后令 \(lst = cur\) 就完成了插入字符的过程。事实上代码并不长,具体如下。
qwq
il void init(){newnode(0); lst = 1;}
il void add(int c){
int cur = newnode(len[lst] + 1); int p = lst; lst = cur; ed[cur] = 1;
while(!son[p][c]) son[p][c] = cur, p = fail[p];
if(!p){fail[cur] = 1; return;}
int q = son[p][c];
if(len[p] + 1 == len[q]){fail[cur] = q; return;}
int nq = newnode(len[p] + 1);
cpy(son[nq], son[q], S); fail[nq] = fail[q]; fail[q] = fail[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fail[p];
}
节点个数大概是 \(2n\) 级别的,转移数量大概是 \(3n\) 级别的,时间复杂度是 \(O(n)\) 的,证明是不会的。如果想要了解,可以看魏老师的博客。
然后还有一个问题,如何求 \(\operatorname{endpos}\) 集合呢?注意到 \(fail\) 树上每个节点 \(u\) 的 \(\operatorname{endpos}\) 集合实际上是所有儿子 \(\operatorname{endpos}\) 的并,于是可以离线下来使用线段树合并(\(O(n \log n)\))/ set 启发式合并(\(O(n \log^2 n)\))。但是事实上,如果只需要求 \(\operatorname{endpos}\) 集合的大小,只需要记 \(ed_u = \sum_{fail_v = u} ed_v\) 即可,令叶子节点 \(ed_u = 1\)。
经典例题
也可能是一些经典套路。
P3804 【模板】后缀自动机(SAM)
出现次数就是 \(\operatorname{endpos}\) 集合大小。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
#define cpy(x, y, s) memcpy(x, y, sizeof(x[0]) * (s))
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10, S = 26;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int n;
namespace SAM{
int son[N][S], fail[N], tot, ed[N], len[N], lst, buc[N], id[N];
il int newnode(int lll){int o = ++tot; len[o] = lll; memset(son[o], 0, sizeof son[o]); fail[o] = 0; return o;}
il void init(){newnode(0); lst = 1;}
il void add(int c){
int cur = newnode(len[lst] + 1); int p = lst; lst = cur; ed[cur] = 1;
while(!son[p][c]) son[p][c] = cur, p = fail[p];
if(!p){fail[cur] = 1; return;}
int q = son[p][c];
if(len[p] + 1 == len[q]){fail[cur] = q; return;}
int nq = newnode(len[p] + 1);
cpy(son[nq], son[q], S); fail[nq] = fail[q]; fail[q] = fail[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fail[p];
}
void build(){
for(int i = 1; i <= tot; i++) buc[len[i]]++;
for(int i = 1; i <= n; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = tot; i; i--) ed[fail[id[i]]] += ed[id[i]];
}
} using namespace SAM;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
init();
string str; cin >> str; n = str.size(); str = "*" + str;
for(int i = 1; i <= n; i++) add(str[i] - 'a'); ll ans = 0; build();
for(int i = 1; i <= tot; i++) chkmax(ans, 1ll * (ed[i] > 1) * ed[i] * len[i]);
cout << ans;
return 0;
}
P3975 TJOI2015 弦论
- 题意:给定字符串 \(S\),问它的第 \(k\) 小字符串(当参数 \(t = 0\) 时为本质不同的字符串,否则出现位置不同也算作不同)
令 \(f_u = \sum_{v \in \delta(u)} f_v + 1 / ed_u\),每次通过 \(k\) 与 \(f_v\) 的大小快速跳过某个 \(v\),然后 \(\mathrm {dfs}\) 一遍即可。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
#define int long long
using namespace std;
const int N = 1e6 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
//il void chkmin(int& x, int y){if(y < x) x = y;}
//il void chkmax(int& x, int y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int t, n;
namespace SAM{
int len[N], fail[N], tot, lst, son[N][26], buc[N], id[N], vis[N];
ll f[N], ed[N];
void init(){tot = lst = 1;}
ll getval(int p){return (t ? ed[p] : 1ll);}
void add(int c){
int cur = ++tot, p = lst; len[cur] = len[lst] + 1; lst = cur; ed[cur] = 1;
while(!son[p][c]) son[p][c] = cur, p = fail[p];
if(!p) return fail[cur] = 1, void();
int q = son[p][c];
if(len[p] + 1 == len[q]) return fail[cur] = q, void();
int nq = ++tot; len[nq] = len[p] + 1; memcpy(son[nq], son[q], sizeof son[nq]);
fail[nq] = fail[q]; fail[q] = fail[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fail[p];
}
void dfs(int u){
vis[u] = 1;
for(int i = 0; i < 26; i++){
if(!son[u][i]) continue;
if(!vis[son[u][i]]) dfs(son[u][i]);
f[u] += f[son[u][i]];
}
if(u != 1) f[u] += getval(u);
}
void build(){
for(int i = 1; i <= tot; i++) buc[len[i]]++;
for(int i = 1; i <= n; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = tot; i; i--) ed[fail[id[i]]] += ed[id[i]];
}
void getans(int p, int k){
//cerr << f[p] << " " << k << "\n";
if(f[p] < k){cout << -1; return;}
if(p != 1){
if(k <= getval(p)) return;
k -= getval(p);
}
//cerr << p << " " << k << "\n";
for(int i = 0; i < 26; i++){
//cerr << "\n" << p << " " << i << " " << son[p][i] << "\n";
if(!son[p][i]) continue;
if(f[son[p][i]] < k){k -= f[son[p][i]]; continue;}
cout << (char)(i + 'a'); getans(son[p][i], k); break;
}
}
};
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
string str; cin >> str; n = str.size(); str = "*" + str; SAM::init();
for(int i = 1; i <= n; i++) SAM::add(str[i] - 'a'); SAM::build();
int k; cin >> t >> k;
SAM::dfs(1); SAM::getans(1, k);
return 0;
}
P4482 BJWC2018 Border 的四种求法
由于听说这个题是经典题,遂来做。
首先考虑一个方便 \(\rm SAM\) 上刻画 \(\rm Border\) 的条件:令 \(\operatorname{LCS}(i, j)\) 为串 \(S[1\dots i]\) 与 \(S[1\dots j]\) 的最长公共后缀,那么串 \(S[l\dots i]\) 是 \(S[l \dots r]\) 的 \(\rm Border\) 当且仅当 \(\operatorname{LCS}(l, i) \ge i - l + 1\)。然后注意到 \(\operatorname{LCS}(l, i)\) 相当于 \(edcur_l\) 与 \(edcur_i\) 在 \(\rm parent\ tree\) 上的 \(\rm LCA\) 的 \(len\)(其中 \(edcur_i\) 为 \(S[1\dots i]\) 表示的状态。)于是对于一个询问 \([l, r]\),考虑枚举 \(p = \operatorname{LCS}(i, j)\),那么 \(p\) 一定是 \(edcur_r\) 的某个祖先。
那么考虑 \(p\) 的子树中的所有点的集合 \(S\),接下来 \(i \in S\),相当于找到满足:
- \(l - 1 \ge i - len_p\)
- \(l \le i \le r - 1\)
的最大的 \(i - l + 1\)。(这里其实有可能不满足 \(\operatorname{LCS}(i, r) = p\),即 \(\operatorname{LCS}(i, r)\) 的深度可能更深,但是由于越上面的限制越紧(即 \(len_p\) 越大),于是不影响答案)
接下来把询问离线,遇到一个询问就把他的所有祖先的询问集合加上这个询问。枚举点 \(p\),考虑如何处理他的询问。暴力的想,可以把他的子树所有信息加入一颗线段树中,通过线段树二分每次 \(O(\log n)\) 求出答案。于是这样做的时间复杂度是 \(O(\sum{siz_u}\log n)\) 的。
但是注意到每次往上跳的时间复杂度是很劣的,于是考虑优化这个过程,于是考虑重链剖分。每次只把询问 \([l, r]\) 挂在 \(ed_r\) 向上跳的时候经过 \(O(\log n)\) 条重链 访问到的首个节点,即对 \(ed_r \to T\) 重链剖分后重链的 链底处。于是这些询问相当于要求在这个重链上的某个前缀信息,于是接下来单独 从上到下 处理每条重链所挂的询问。
单独拎出一条重链,那么从上到下遍历每一个重链上的点 \(p\),但是显然不能每次把所有子树的信息全部考虑。观察一下下面树的形态可以发现,对于重链上的点,如果其不是询问 \([l, r]\) 剖分后 链底 的那个点,那么若 \(i\) 在其重子树中,显然不如底端的点优,所以对于非底端的点,只需要考虑 \(i\) 在其轻子树中的情况。而对于所有轻子树,其 \(\sum{siz} = O(n \log n)\)(每次考虑一个点 \(x\) 对轻子树的贡献,显然是 \(x \to T\) 上轻边的数量,而这是 \(O(\log n)\) 的),于是每次暴力加入线段树即可,并依次回答询问即可。
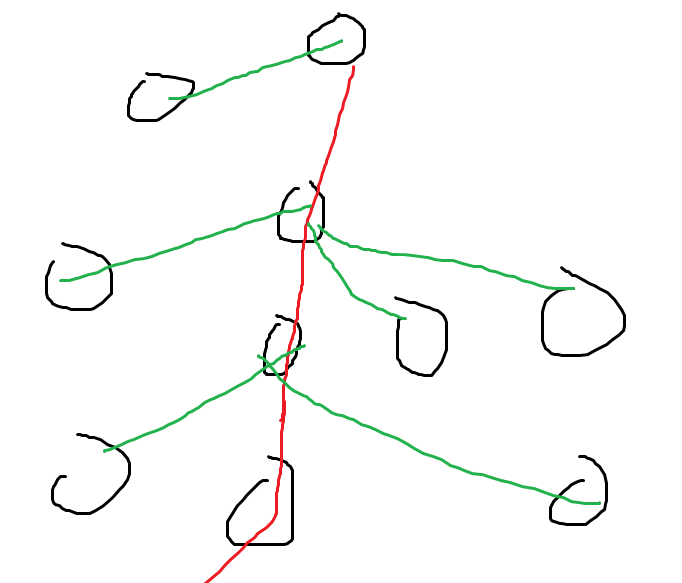
但是对于底端的点怎么办呢?注意到这样的点只有 \(O(q \log n)\) 个,我们需要的是对于询问 \([l, r]\) 以及底端的点 \(p\),查询对于 \(S[1\dots r]\) 的长度为 \([\operatorname{minlen}(p), \operatorname{len}(p)]\) 的后缀中长度最长的 \(\rm Border\),其中这些后缀满足 \(\operatorname{endpos}\) 集合相同。若我们每次可以快速求出答案就可以完成了。但是之前的刻画 \(\rm Border\) 方式不太让我们快速完成单次判定,考虑使用 \(\operatorname{endpos}\) 进行刻画。不难发现对于询问 \([l, r]\) 以及底端的点 \(p\),若 \(\operatorname{endpos}(p) \cap [l, l + len_p - 1] = Q\),则对于 \(i \in Q\),\([l, i]\) 就是一个 \(S[l \dots r]\) 的 \(\rm Border\)。于是使用可持久化线段树合并就可以做到每次 \(O(\log n)\) 查询最长 \(\rm Border\) 的长度。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
using namespace std;
const int N = 4e5 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
struct edge{
int v, next;
}edges[N << 1];
int head[N], idx;
void add_edge(int u, int v){
edges[++idx] = {v, head[u]};
head[u] = idx;
}
int n, q, INF;
int son[N], siz[N], top[N];
vector<int> chain[N];
int ed[N], edcur[N];
int ANS[N];
struct query{
int l, r, id;
};
vector<query> Q[N];
struct Segtree1{
#define mid ((l + r) >> 1)
struct node{
int ls, rs, mx;
}tn[N << 5];
int rt[N], tot;
void pushup(int o){tn[o].mx = max(tn[tn[o].ls].mx, tn[tn[o].rs].mx);}
void add(int& o, int l, int r, int x){
if(!o) o = ++tot;
if(l == r){chkmax(tn[o].mx, x); return;}
if(x <= mid) add(tn[o].ls, l, mid, x);
else add(tn[o].rs, mid + 1, r, x);
pushup(o);
}
int getmx(int o, int l, int r, int s, int t){
if(!o || s > t) return 0;
if(s <= l && r <= t) return tn[o].mx;
int val = 0;
if(s <= mid) chkmax(val, getmx(tn[o].ls, l, mid, s, t));
if(mid < t) chkmax(val, getmx(tn[o].rs, mid + 1, r, s, t));
return val;
}
int merge(int x, int y, int l, int r){
if(!x || !y) return x + y;
int nw = ++tot;
if(l == r) tn[nw].mx = max(tn[x].mx, tn[y].mx);
tn[nw].ls = merge(tn[x].ls, tn[y].ls, l, mid);
tn[nw].rs = merge(tn[x].rs, tn[y].rs, mid + 1, r);
pushup(nw); return nw;
}
void dfs(int o, int l, int r){
if(!o) return;
if(l == r) cerr << o << " " << l << "\n";
dfs(tn[o].ls, l, mid); dfs(tn[o].rs, mid + 1, r);
}
void dbg(int o){dfs(o, 1, n);}
}endpos;
struct Segtree2{
#define ls (o << 1)
#define rs (o << 1 | 1)
#define mid ((l + r) >> 1)
vector<int> rub;
int mn[N << 2];
Segtree2(){memset(mn, 0x3f, sizeof mn); INF = mn[1];}
void pushup(int o){mn[o] = min(mn[ls], mn[rs]);}
void modify(int o, int l, int r, int x, int k){
rub.pb(o);
if(l == r) return chkmin(mn[o], k), void();
if(x <= mid) modify(ls, l, mid, x, k);
else modify(rs, mid + 1, r, x, k);
pushup(o);
}
int getans(int o, int l, int r, int s, int t, int lim){
if(l > t || r < s || mn[o] > lim) return -1;
if(l == r) return l;
if(s <= l && r <= t){
if(mn[rs] <= lim) return getans(rs, mid + 1, r, s, t, lim);
return getans(ls, l, mid, s, t, lim);
}
int ret = getans(rs, mid + 1, r, s, t, lim);
if(ret != -1) return ret;
return getans(ls, l, mid, s, t, lim);
}
}tr;
namespace SAM{
int tot, lst, len[N], fa[N], son[N][26];
void init(){lst = tot = 1;}
void add(int c){
int cur = ++tot, p = lst; len[cur] = len[lst] + 1; lst = cur;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][c];
if(len[q] == len[p] + 1) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; len[nq] = len[p] + 1; memcpy(son[nq], son[q], sizeof son[nq]);
fa[q] = fa[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
};
using SAM::fa;
using SAM::len;
void dfs1(int u){
siz[u] = 1;
for(int i = head[u]; i; i = edges[i].next){
int v = edges[i].v; if(v == fa[u]) continue;
dfs1(v); siz[u] += siz[v];
endpos.rt[u] = endpos.merge(endpos.rt[u], endpos.rt[v], 1, n);
//if(u == 10) cerr << v << "\n";
if(siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int tp){
chain[tp].pb(u); top[u] = tp;
if(son[u]) dfs2(son[u], tp);
else return;
for(int i = head[u]; i; i = edges[i].next) if(edges[i].v != fa[u] && edges[i].v != son[u]) dfs2(edges[i].v, edges[i].v);
}
void upd(int u, int lc){
if(ed[u]) tr.modify(1, 1, n, ed[u], ed[u] - lc);
for(int i = head[u]; i; i = edges[i].next){
int v = edges[i].v; if(v == fa[u]) continue;
upd(v, lc);
}
}
void build(){
for(int i = 2; i <= SAM::tot; i++) add_edge(fa[i], i), add_edge(i, fa[i]);
for(int i = 2; i <= SAM::tot; i++) if(ed[i]) endpos.add(endpos.rt[i], 1, n, ed[i]);//, cerr << i << "\n", endpos.dbg(endpos.rt[i]), cerr << "\n";
dfs1(1); dfs2(1, 1);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
SAM::init();
string str; cin >> str; n = str.size(); str = "*" + str;
for(int i = 1; i <= n; i++) SAM::add(str[i] - 'a'), edcur[i] = SAM::lst, ed[SAM::lst] = i;//, cerr << edcur[i] << " " << fa[edcur[i]] << "\n";
build(); //endpos.dbg(endpos.rt[10]);
cin >> q;
for(int i = 1; i <= q; i++){
int l, r; cin >> l >> r;
if(l == r) continue;
int p = edcur[r];
while(p > 1){
chkmax(ANS[i], endpos.getmx(endpos.rt[p], 1, n, l, min(r - 1, l + len[p] - 1)) - l + 1);
//cerr << ed[p] << " " << endpos.getmx(endpos.rt[p], 1, n, l, min(r - 1, l + len[p] - 1) - l + 1) << "\n";
//cerr << endpos.getmx(endpos.rt[p], 1, n, 1, n) << "\n";
Q[p].pb((query){l, r, i});
p = fa[top[p]];
}
}
for(int i = 1; i <= n; i++){
for(auto u : chain[i]){
if(ed[u]) tr.modify(1, 1, n, ed[u], ed[u] - len[u]);
for(int j = head[u]; j; j = edges[j].next){
int v = edges[j].v;
if(v != son[u] && v != fa[u]) upd(v, len[u]);
}
for(auto qu : Q[u]){
int l = qu.l, r = qu.r, id = qu.id;
chkmax(ANS[id], tr.getans(1, 1, n, l, r - 1, l - 1) - l + 1);
}
}
for(auto u : tr.rub) tr.mn[u] = INF; tr.rub.clear();
}
for(int i = 1; i <= q; i++) cout << ANS[i] << "\n";
return 0;
}
P6640 BJOI2020 封印
终于有一道自己想出来的 \(\rm SAM\) 非板子题了,开心。
首先考虑如何做 \([1, n]\) 的询问。那么可以把 \(T\) 的 \(\rm SAM\) 建出来,然后把 \(S\) 放上去跑,每次匹配出来的状态就是 \(S[1 \dots i]\) 最长的后缀 且 满足这个后缀是 \(T\) 的某个子串。于是一路跑取 \(\max\) 即可。那么令 \(g_i\) 为跑到 \(i\) 时,所得到的状态的长度。那么对于询问 \([l, r]\),答案就是 \(\max_{i = l}^r{\min(i - l + 1, g_i)}\)。
考虑拆 \(\min\),当 \(g_i - i \le -l\) 时,可以取到 \(g_i\)。同时注意到当 \(i \to i + 1\),\(-i\) 一定变小一,但是 \(g_i\) 不一定变大一,于是 \(t_i = g_i - i\) 单调不升。那么可以通过二分找出一个后缀 \([m, i]\) 满足 \(g_i \le i - l + 1\),那么通过 st 表就可以快速回答询问。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
using namespace std;
const int N = 2e5 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int n, m, qwq[N];
namespace SAM{
const int SM = N << 1;
int tot, lst, len[SM], fail[SM], son[SM][2];
void init(){tot = lst = 1;}
void add(int c){
int cur = ++tot, p = lst; len[cur] = len[lst] + 1; lst = cur;
while(!son[p][c]) son[p][c] = cur, p = fail[p];
if(!p) return fail[cur] = 1, void();
int q = son[p][c];
if(len[q] == len[p] + 1) return fail[cur] = q, void();
int nq = ++tot; len[nq] = len[p] + 1; fail[nq] = fail[q]; memcpy(son[nq], son[q], sizeof son[q]);
fail[q] = fail[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fail[p];
}
void getmat(string str){
m = str.size(); str = "*" + str; int p = 1, plen = 0;
for(int i = 1; i <= m; i++){
int c = str[i] -'a';
if(!son[p][c]){
while(p > 1 && !son[p][c]) p = fail[p];
plen = len[p];
}
if(son[p][c]) p = son[p][c], plen++;
qwq[i] = plen; //cerr << qwq[i] << " ";
}
}
};
int mn[N][19], lg2[N];
int qry(int l, int r){
int len = lg2[r - l + 1];
return max(mn[r][len], mn[l + (1ll << len) - 1][len]);
}
void solve(){
int l, r; cin >> l >> r;
int L = l, R = r, res = r + 1; //cerr << res << "\n";
while(L <= R){
int mid = (L + R >> 1);
if(qwq[mid] - mid <= -l) res = mid, R = mid - 1;
else L = mid + 1;
} //cerr << res << "\n";
int ans = 0;
if(res != r + 1) chkmax(ans, qry(res, r));
chkmax(ans, res - l);
cout << ans << "\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
SAM::init();
string s, t; cin >> t >> s; n = s.size(); s = "*" + s;
for(int i = 1; i <= n; i++) SAM::add(s[i] - 'a');
SAM::getmat(t);
for(int i = 2; i <= m; i++) lg2[i] = lg2[i >> 1] + 1;
for(int i = 1; i <= m; i++){
mn[i][0] = qwq[i]; //cerr << qwq[i] - i << "\n";
for(int j = 1; (1ll << j) <= i; j++) mn[i][j] = max(mn[i][j - 1], mn[i - (1ll << (j - 1))][j - 1]);
}
int T; cin >> T; while(T--) solve();
return 0;
}
P5576 [CmdOI2019] 口头禅
首先考虑 \(\rm {LCS2}\) 的做法,选一个串作为匹配串 \(T\),然后对其他文本串都建一个 \(\rm SAM\),每次把 \(T\) 放进去跑,然后跑出来 \(g_{s, i}\) 是 \(T[1\dots i]\) 在第 \(s\) 个文本串中出现的最长后缀,即 \(T[{i - g_i + 1} \dots i]\) 在 \(S_s\) 中出现过,且 \(g_i\) 最大。这个时间复杂度是 \(O(|T|n + \sum{len})\)。如果选择 \(|T|\) 最小的串,那么由于 \(\min\{len\} \times n \le \sum{len}\),于是最后时间复杂度是 \(O(n)\) 的。
然后考虑如何快速回答询问,由于没有修改且可以离线,于是可以考虑猫树分治。每次选择其中一个分界点 \(mid\),考虑跨过 \(mid\) 的询问。然后把 \(S_{mid}\) 作为匹配串 \(T\),往两边跑 \(g\) 前后缀的 \(\min\)。对于每个询问合并即可。然后这里的时间复杂度是 \(O(O(E) \times {dep} + \sum{len})\),其中 \(O(E)\) 是处理一层的时间复杂度。合并一个询问的时间复杂度是 \(O(|T|)\) 的。发现这个东西与 \(|T|\) 的长度很有关,于是可以每次选择区间中的任意一个最短串,然后还要深度较小,于是选择这些串中间的那个,于是一个最小值只会递归 \(O(\log n)\) 次,有至多 \(O(\sqrt {\sum len})\) 个不同的值,这样分治树的高度就是两者相乘。但由于一个 \(x\) 作为区间最小值的区间长度只有 \(\frac{\sum{len}}{x}\),于是 \(O(E) = O(\sum{len})\)。然后考虑合并的时间复杂度。考虑最坏情况,假设现在 \(len\) 降序排序,且询问不重,于是有这个柿子:
假设前 \(\sqrt q\) 个串达到了 \(O(\sum {len})\),但是由于降序排序的原因,这样至多是 \(O(q \sqrt {\sum {len}})\) 的。
那么这样做的时间复杂度是 \(O(\sum{len} \times \sqrt {\sum len} \log n + q \sqrt {\sum {len}})\) 的。这个东西过不去,后面的东西其实够优秀了,但是分治树太高了。注意到我们每次不一定真的要选最小值,而是选择与最小值同阶的别的串。具体的,我们设置一个阈值基数 \(c\) 以及当前阈值指数 \(lim\),当考虑到 \([l, r]\) 时,把长度为 \([c^{lim}, c^{lim + 1})\) 的串都看做 一种最小值 做一遍。如果没有,那么令 \(lim = lim + 1\) 继续做即可。那么这样只会有 \(O(log_c \sum{len})\) 个不同的最小值。每种 最小值只递归 \(O(\log n)\) 层。但是匹配的时间复杂度为 \(O(c |T|)\)。时间复杂度为 \(O(c\sum{len} \times \log n \log_c \sum_{len} + c \times q \sqrt {\sum{len}})\)。
当 \(c = 2\) 时,效率很高,于是被称为 倍增分治。
代码中的阈值为 \(5\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 2e4 + 10, M = 4e5 + 10, QN = 1e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
il void chkmin(vector<int>& ths, vector<int> qwq){
int lll = ths.size();
for(int i = 0; i < lll; i++) chkmin(ths[i], qwq[i]);
}
int n, len[N], Q;
int qrt[QN], qrl[QN], qrr[QN], node[N], ANS[QN], id[QN], pw[25];
string strT[N];
vector<int> sl[N], sr[N];
struct query{
int l, r, id;
}q[QN];
map<pir, int> f;
namespace SAMsp{
const int SN = M << 1;
int tot, len[SN], fa[SN], son[SN][2];
struct SAM{
int lst, rt;
void init(){lst = rt = ++tot;}
void add(int c){
int cur = ++tot, p = lst; len[cur] = len[lst] + 1; lst = cur;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = rt, void();
int q = son[p][c];
if(len[p] == len[q] + 1) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; memcpy(son[nq], son[q], sizeof son[nq]);
len[nq] = len[p] + 1; fa[cur] = fa[q] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
vector<int> getmat(string s){
int p = rt, plen = 0, n = s.size();
vector<int> ans(n);
for(int i = 0; i < n; i++){
int c = s[i] - '0';
if(!son[p][c]){
while(p != rt && !son[p][c]) p = fa[p];
plen = len[p];
}
if(son[p][c]) p = son[p][c], plen++;
ans[i] = plen;
} return ans;
}
}tr[N];
};
using SAMsp::tr;
void clr(){
qrt[0] = qrl[0] = qrr[0] = node[0] = 0;
}
void solve(int l, int r, int ql, int qr, int lim){
//cerr << l << " " << r << " " << ql << " " << qr << " " << lim << "\n";
//for(int i = ql; i <= qr; i++) cerr << id[i] << "\n";
if(l > r || ql > qr) return;
int L, R; clr();
while(1){
L = pw[lim], R = pw[lim + 1] - 1;
for(int i = l; i <= r; i++) if(L <= len[i] && len[i] <= R) node[++node[0]] = i;
assert(lim <= 25);
if(node[0]) break; lim++;
} int mid = node[(1 + node[0]) >> 1];
for(int i = mid; i >= l; i--){
vector<int> ths; ths = tr[i].getmat(strT[mid]);
if(i != mid) sl[i] = sl[i + 1], chkmin(sl[i], ths);
else sl[i] = ths;
}
for(int i = mid; i <= r; i++){
vector<int> ths; ths = tr[i].getmat(strT[mid]);
if(i != mid) sr[i] = sr[i - 1], chkmin(sr[i], ths);
else sr[i] = ths;
}
for(int i = ql; i <= qr; i++){
auto qaq = q[id[i]];
int qwql = qaq.l, qwqr = qaq.r;
//if(id[i] == 5) cerr << (qwqr < mid) << "\n";
if(qwql <= mid && mid <= qwqr) qrt[++qrt[0]] = id[i];
else if(qwqr < mid) qrl[++qrl[0]] = id[i];
else qrr[++qrr[0]] = id[i];
} //cerr << qrt[0] << " " << qrl[0] << " " << qrr[0] << "\n";
for(int i = 1; i <= qrt[0]; i++){
auto qaq = q[qrt[i]];
int qwql = qaq.l, qwqr = qaq.r;
pir ths = mkpir(qwql, qwqr);
if(f.count(ths)){ANS[qaq.id] = f[ths]; continue;}
int ret = 0; vector<int> gg; gg = sl[qwql]; chkmin(gg, sr[qwqr]);
for(auto v : gg) chkmax(ret, v);
ANS[qaq.id] = f[ths] = ret;
} //cerr << qrr[0] << "\n";
for(int i = ql; i < ql + qrl[0]; i++) id[i] = qrl[i - ql + 1];
for(int i = qr; i > qr - qrr[0]; i--) id[i] = qrr[qr - i + 1];
int tmp = qrr[0]; // !
solve(l, mid - 1, ql, ql + qrl[0] - 1, lim); solve(mid + 1, r, qr - tmp + 1, qr, lim);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> Q;
for(int i = 1; i <= n; i++){
cin >> strT[i]; len[i] = strT[i].size();
tr[i].init();
for(int j = 0; j < len[i]; j++) tr[i].add(strT[i][j] - '0');
} //cerr << 1 << "\n";
for(int i = 1; i <= Q; i++){
id[i] = q[i].id = i;
cin >> q[i].l >> q[i].r;
}
pw[0] = 1;
for(int i = 1; i < 25; i++) pw[i] = pw[i - 1] * 5;
solve(1, n, 1, Q, 0);
for(int i = 1; i <= Q; i++) cout << ANS[i] << "\n";
return 0;
}
P4770 NOI2018 你的名字
首先考虑 \(l = 1, r = n\) 怎么做,答案 = \(T\) 本质不同的子串数量 - \(T\) 在 \(S\) 中出现的本质不同子串个数。那么建出 \(T\) 的 \(\rm SAM\),算出 \(\rm T\) 本质不同的子串数量。然后对于 \(T\) 在 \(S\) 中出现的本质不同的子串个数,可以把 \(T\) 丢进 \(S\) 的 \(\rm SAM\) 中跑,得出 \(plen_i\) 为满足 \(T[i - x + 1 \dots i]\) 在 \(S\) 中出现过的最大 \(x\)。然后令 \(lim_u\) 表示节点 \(u\) 所表示的所有子串中,长度 \(\le lim_u\) 在 \(S\) 中出现过。求这个东西只需要 \(\forall i, lim_{edTcur_i} = plen_i\)。其中 \(edTcur_i\) 是 \(T\) 的 \(\rm SAM\) \([1\dots i]\) 的终止状态。然后对于剩下的节点,\(lim_u = \max_{v \in \operatorname{subtree}(u)} {lim_v}\)。
68 分代码
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int n, m, mtlen[N], edTcur[N], lim[N];
struct SAM_S{
#define minlen(u) (len[fa[u]] + 1)
int tot, lst, son[N][26], len[N], fa[N], buc[N], id[N], siz;
void init(){tot = lst = 1;}
void add(int c){
int cur = ++tot, p = lst; lst = cur; len[cur] = len[p] + 1; siz++;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][c];
if(len[p] + 1 == len[q]) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; memcpy(son[nq], son[q], sizeof son[q]);
len[nq] = len[p] + 1; fa[q] = fa[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
void sort(){
for(int i = 1; i <= tot; i++) buc[len[i]]++;
for(int i = 1; i <= siz; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = 1; i <= siz; i++) buc[i] = 0;
}
void getmat(string T){
int p = 1, plen = 0;
for(int i = 1; i < T.size(); i++){
int c = T[i] - 'a';
while(p > 1 && !son[p][c]) p = fa[p], plen = len[p];
if(son[p][c]) p = son[p][c], plen++;
chkmax(lim[edTcur[i]], plen);
//cerr << edTcur[i] << ' ' << plen << "\n";
}
}
}trS;
struct SAM_T{
#define minlen(u) (len[fa[u]] + 1)
int tot, lst, son[N][26], len[N], fa[N], buc[N], id[N], siz;
void init(){for(int i = 1; i <= tot; i++) len[i] = fa[i] = lim[i] = 0, memset(son[i], 0, sizeof son[i]); tot = lst = 1; siz = 0;}
void add(int c){
int cur = ++tot, p = lst; lst = cur; len[cur] = len[p] + 1; siz++;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][c];
if(len[p] + 1 == len[q]) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; memcpy(son[nq], son[q], sizeof son[q]);
len[nq] = len[p] + 1; fa[q] = fa[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
void build(string str){
init();
for(int i = 1; i < str.size(); i++) add(str[i] - 'a'), edTcur[i] = lst;
}
void sort(){
for(int i = 1; i <= tot; i++) buc[len[i]]++;
for(int i = 1; i <= siz; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = 1; i <= siz; i++) buc[i] = 0;
}
ll getans(){
for(int i = tot; i; i--) chkmax(lim[fa[id[i]]], lim[id[i]]);
ll ans = 0;
for(int i = 1; i <= tot; i++) ans -= max(0, min(lim[i], len[i]) - minlen(i) + 1), ans += len[i] - len[fa[i]];
return ans;
}
}trT;
void solve(){
string str;int l, r; cin >> str >> l >> r; m = str.size(); str = "*" + str;
trT.build(str); trT.sort(); trS.getmat(str);
cout << trT.getans() << "\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
string str; cin >> str; n = str.size(); str = "*" + str;
trS.init();
for(int i = 1; i <= n; i++) trS.add(str[i] - 'a');
trS.sort();
int T; cin >> T; while(T--) solve();
return 0;
}
时间复杂度是 \(O(|S| + \sum |T|)\) 的。
注意到对于限制只能取 \(S[l\dots r]\) 的一般情况,只对匹配过程中有影响。进一步的,我们只需要求一个 \(S\) 的 \(\rm SAM\) 的节点 \(u\) 在 \([l, r]\) 中出现的最长长度,那么我们可持久化线段树合并出 \(\operatorname{endpos}(u)\),于是 \(u\) 在 \([l, r]\) 中出现的最右位置即为 \(\operatorname{endpos} (u)\) 中 \([l + \operatorname{minlen}(u) - 1, r]\) 的最大值。这样我们就在时间复杂度 \(O(|S| \log |S| + \sum |T|)\),空间复杂度 \(O(|S| \log |S| + \max |T|)\) 的情况下解决了此题。
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
#define pir pair<int, ll>
#define fi first
#define second se
#define inv(x) qpow(x, mod - 2)
#define il inline
#define mkpir make_pair
using namespace std;
const int N = 2e6 + 10, M = 2e5 + 10;
const ll mod = 998244353;
il ll qpow(ll& x, ll y){
ll ret = 1;
for(; y; y >>= 1, x = x * x % mod) if(y & 1) ret = ret * x % mod;
return ret;
}
il void chkmin(ll& x, ll y){if(y < x) x = y;}
il void chkmin(int& x, int y){if(y < x) x = y;}
il void chkmax(int& x, int y){if(y > x) x = y;}
il void chkmax(ll& x, ll y){if(y > x) x = y;}
il void ADD(ll& x, ll y){x += y; (x >= mod) ? (x -= mod) : 0;}
il void MUL(ll& x, ll y){x = x * y % mod;}
int n, m, mtlen[N], edTcur[N], lim[N];
struct SAM_S{
#define minlen(u) (len[fa[u]] + 1)
int tot, lst, son[N][26], len[N], fa[N], buc[N], id[N], siz, ed[N];
struct Segtree{
#define mid ((l + r) >> 1)
struct node{
int ls, rs, mx;
}tn[N << 5];
int cnt, rt[N];
il void pushup(int o){tn[o].mx = max(tn[tn[o].ls].mx, tn[tn[o].rs].mx);}
il void add(int& o, int l, int r, int x){
tn[o = ++cnt].mx = x;
if(l == r) return;
if(x <= mid) add(tn[o].ls, l, mid, x);
else add(tn[o].rs, mid + 1, r, x);
}
il int merge(int o, int root, int l, int r){
if(!o || !root) return o + root;
int z = ++cnt;
if(l == r){tn[z].mx = max(tn[o].mx, tn[root].mx); return z;}
tn[z].ls = merge(tn[o].ls, tn[root].ls, l, mid);
tn[z].rs = merge(tn[o].rs, tn[root].rs, mid + 1, r);
pushup(z); return z;
}
il int getmax(int o, int l, int r, int s, int t){
if(s > t) return -1;
if(s <= l && r <= t) return tn[o].mx;
if(!o) return -1;
int ret = -1;
if(s <= mid) chkmax(ret, getmax(tn[o].ls, l, mid, s, t));
if(mid < t) chkmax(ret, getmax(tn[o].rs, mid + 1, r, s, t));
return ret;
}
}endp;
il void init(){tot = lst = 1;}
il void add(int c){
int cur = ++tot, p = lst; lst = cur; len[cur] = len[p] + 1; ed[cur] = ++siz;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][c];
if(len[p] + 1 == len[q]) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; memcpy(son[nq], son[q], sizeof son[q]);
len[nq] = len[p] + 1; fa[q] = fa[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
il void sort(){
for(int i = 1; i <= tot; i++){
buc[len[i]]++;
if(ed[i]) endp.add(endp.rt[i], 1, n, ed[i])/*, cerr << endp.getmax(endp.rt[i], 1, n, ed[i], ed[i])*/;
}
for(int i = 1; i <= siz; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = 1; i <= siz; i++) buc[i] = 0;
for(int i = tot; i; i--){
int x = id[i];
endp.rt[fa[x]] = endp.merge(endp.rt[fa[x]], endp.rt[x], 1, n);
}
}
int getpos(int p, int l, int r){return endp.getmax(endp.rt[p], 1, n, l + minlen(p) - 1, r);}
int ex(int p, int l, int r){
if(p == 0) return 0;
int R = getpos(p, l, r);
//cerr << ed[9] << " " << len[p] << " " << R << "\n";
if(R < l) return 0;
return min(len[p], R - l + 1);
}
il void getmat(string T, int l, int r){
int p = 1, plen = 0;
for(int i = 1; i < T.size(); i++){
int c = T[i] - 'a';
while(p > 1 && !ex(son[p][c], l, r)) p = fa[p], plen = ex(p, l, r);
//cerr << p << "\n";
int val = ex(son[p][c], l, r); //cerr << val << "\n";
if(val) p = son[p][c], plen++, chkmin(plen, val);//, cerr << "qwq" << "\n";
chkmax(lim[edTcur[i]], plen);
//cerr << p << ' ' << plen << "\n";
}
}
}trS;
struct SAM_T{
#define minlen(u) (len[fa[u]] + 1)
int tot, lst, son[N][26], len[N], fa[N], buc[N], id[N], siz;
il void init(){for(int i = 1; i <= tot; i++) len[i] = fa[i] = lim[i] = 0, memset(son[i], 0, sizeof son[i]); tot = lst = 1; siz = 0;}
il void add(int c){
int cur = ++tot, p = lst; lst = cur; len[cur] = len[p] + 1; siz++;
while(!son[p][c]) son[p][c] = cur, p = fa[p];
if(!p) return fa[cur] = 1, void();
int q = son[p][c];
if(len[p] + 1 == len[q]) return fa[cur] = q, void();
int nq = ++tot; fa[nq] = fa[q]; memcpy(son[nq], son[q], sizeof son[q]);
len[nq] = len[p] + 1; fa[q] = fa[cur] = nq;
while(son[p][c] == q) son[p][c] = nq, p = fa[p];
}
il void build(string str){
init();
for(int i = 1; i < str.size(); i++) add(str[i] - 'a'), edTcur[i] = lst;
}
il void sort(){
for(int i = 1; i <= tot; i++) buc[len[i]]++;
for(int i = 1; i <= siz; i++) buc[i] += buc[i - 1];
for(int i = tot; i; i--) id[buc[len[i]]--] = i;
for(int i = 1; i <= siz; i++) buc[i] = 0;
}
il ll getans(){
for(int i = tot; i; i--) chkmax(lim[fa[id[i]]], lim[id[i]]);
ll ans = 0;
for(int i = 1; i <= tot; i++) ans -= max(0, min(lim[i], len[i]) - minlen(i) + 1), ans += len[i] - len[fa[i]];
return ans;
}
}trT;
il void solve(){
string str; int l, r; cin >> str >> l >> r; m = str.size(); str = "*" + str;
trT.build(str); trT.sort(); trS.getmat(str, l, r);
cout << trT.getans() << "\n";
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
string str; cin >> str; n = str.size(); str = "*" + str;
trS.init();
for(int i = 1; i <= n; i++) trS.add(str[i] - 'a');
trS.sort();
int T; cin >> T; while(T--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号