P3640 [APIO2013] 出题人 题解
原题链接
题意简述
提交答案题
你是一个出题人,有两个问题:
-
\(\text{SSSP}\):最短路
点数不超过 \(300\),边权的绝对值小于 \(10^6\),总边数不超过 \(5000\),询问不超过 \(10\) 次
-
\(\text{Mystery}\):无向图染色
点数小于 \(1000\) 且大于 \(70\),边数小于 \(10^6\) 且大于 \(1500\)。
对于每个测试点:
给定源程序 \(A\) 和源程序 \(B\),需要造一组数据使得源程序 \(A\) 能跑过而源程序 \(B\) 不行且整数个数小于 \(T\)。
一个程序是否能跑过一个问题不在意其答案是否正确,仅关心是否超时
| 测试点编号 | \(T\) | 问题 | 源程序 \(A\) | 源程序 \(B\) |
|---|---|---|---|---|
| \(1\) | \(107\) | \(\text{SSSP}\) | \(\text{ModifiedDijkstra}\) | \(\text{FloydWarshall}\) |
| \(2\) | \(2222\) | \(\text{SSSP}\) | \(\text{FloydWarshall}\) | \(\text{OptimizedBellmanFord}\) |
| \(3\) | \(105\) | \(\text{SSSP}\) | \(\text{OptimizedBellmanFord}\) | \(\text{FloydWarshall}\) |
| \(4\) | \(157\) | \(\text{SSSP}\) | \(\text{FloydWarshall}\) | \(\text{ModifiedDijkstra}\) |
| \(5\) | \(1016\) | \(\text{SSSP}\) | \(\text{ModifiedDijkstra}\) | \(\text{OptimizedBellmanFord}\) |
| \(6\) | \(143\) | \(\text{SSSP}\) | \(\text{OptimizedBellmanFord}\) | \(\text{ModifiedDijkstra}\) |
| \(7\) | \(3004\) | \(\text{Mystery}\) | \(\text{Gamble1}\) | \(\text{RecursiveBacktracking}\) |
| \(8\) | \(3004\) | \(\text{Mystery}\) | \(\text{RecursiveBacktracking}\) | \(\text{Gamble2}\) |
解法
首先我们明确一下每个代码算法及其时间复杂度:
| 代码名称 | 算法 | 时间复杂度 |
|---|---|---|
| \(\text{FloydWarshall}\) | \(\text{Floyd}\) | \(\Theta(V^3+Q)\) |
| \(\text{OptimizedBellmanFord}\) | \(\text{Bellman-Ford}\) | \(\Theta(VEQ)\) |
| \(\text{ModifiedDijkstra}\) | \(\text{Dijkstra}\) | \(\Theta(QE+Q\log_2 E)\) |
| \(\text{Gamble1}\) | \(\text{never TLE}\) | \(\Theta(1)\) |
| \(\text{Gamble2}\) | \(\text{always TLE}\) | \(\Theta(\infty)\) |
| \(\text{RecursiveBacktracking}\) | \(\text{Backtrack}\) | 懒得算,挺大的 |
注意这里 \(V\) 是点数,\(E\) 是边数,\(Q\) 是询问数
point 1
目的
卡 \(\text{Floyd}\)
做法
构造 \(V=101\)
显然因为要输出 \(101\) 个点,至少就要 \(101\) 个数。所以我们把每一个点的出度都描述为 \(0\)。
最后询问只需要一个,问题随你,这里使用 0 99
共计 \(105\) 个数
code
为了防止抄袭,所有代码均无 print 函数,望周知。
#include<bits/stdc++.h>
using namespace std;
const int maxv=305,maxq=15;
int V,E,Q;
vector<pair<int,int>> G[maxv];
int s[maxq],t[maxq];
int main(){
V=101;
Q=1;
for(int i=1;i<=Q;i++){
s[i]=0;
t[i]=99;
}
print();
return 0;
}
point 2
目的
卡 \(\text{Bellman-Ford}(\Theta(VEQ))\)
且需要让 \(\text{Floyd}(\Theta(V^3))\) 过
做法
这个点其实看着难卡,实际上不难。
就是要让 \(V\) 恰好为 \(100\)(让 \(\text{Floyd}\) 过),便尽量多加,在 \(10\) 次询问就行了(主要是询问上限为 \(10\))
可以去 oi-wiki 上看一下这个算法的原理,就可以发现如果我们在一条链上狂加自环,这个算法就会被卡飞。
最后的询问要按照你建边的方向,否则卡不掉。
最后算一下边能放多少边:\(E_{\max}=\frac{2222(T)-1(V)-100(出度)-1(Q)-2\times10(询问)}{2(点编号及权值)}-99(链)=951\)
code
#include<bits/stdc++.h>
using namespace std;
const int maxv=305,maxq=15;
int V,E,Q;
vector<pair<int,int>> G[maxv];
int s[maxq],t[maxq];
int main(){
V=100;
E=951;
for(int i=0;i<V;i++){
int k=min(E,10);
E-=k;
if(i!=0){
G[i].push_back(make_pair(i-1,rand()%114514+114514));
}
for(int j=1;j<=k;j++){
G[i].push_back(make_pair(i,rand()%114514+114514));
}
}
Q=10;
for(int i=1;i<=Q;i++){//由于我是反着建的链,所以输出99 0
s[i]=99;
t[i]=0;
}
print();
return 0;
}
point 3
同 point 1,这里不加赘述
point 4
目的
卡 \(\text{Dijkstra}(\Theta(QE+Q\log_2 E))\)
且需要让 \(\text{Floyd}(\Theta(V^3))\) 过
做法
不了解 \(\text{Dijkstra}\) 的可以去 oi-wiki 上看看。我们可以看到:
在稀疏图中,\(m=\Theta(n)\),使用二叉堆实现的 Dijkstra 算法较 Bellman-Ford 算法具有较大的效率优势;而在稠密图中,\(m=\Theta(n^2)\),这时候使用暴力做法较二叉堆实现更优。
但是这个题没有给我们建稠密图的机会,我们不能这么卡。
于是,我们只能从 \(\text{Dijkstra}\) 松弛操作的漏洞来卡。
就如 Abzilurtahv 大佬所说的那样,只要构造出如下图的情况, \(\text{Dijkstra}\) 就去世了。
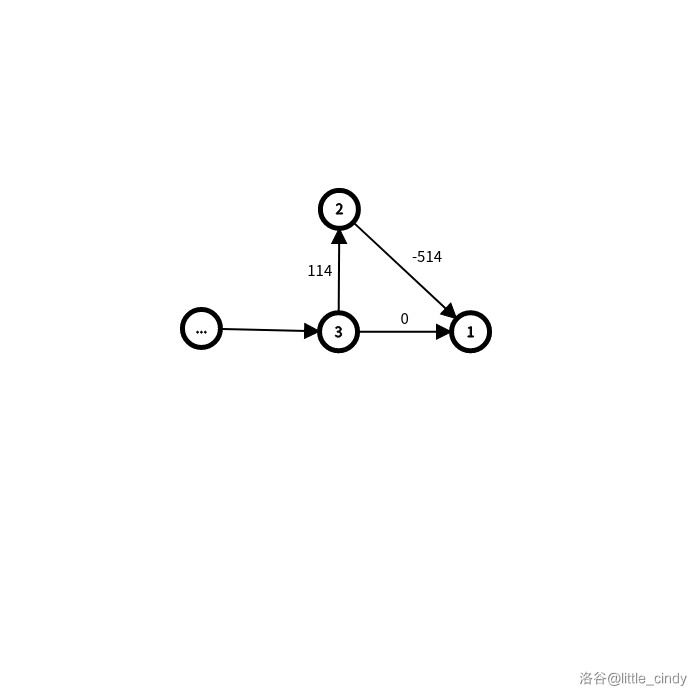
那么为什么?这里是很多题解没有说到的。
我们来简单的证明一下:
我们截取一个片段:
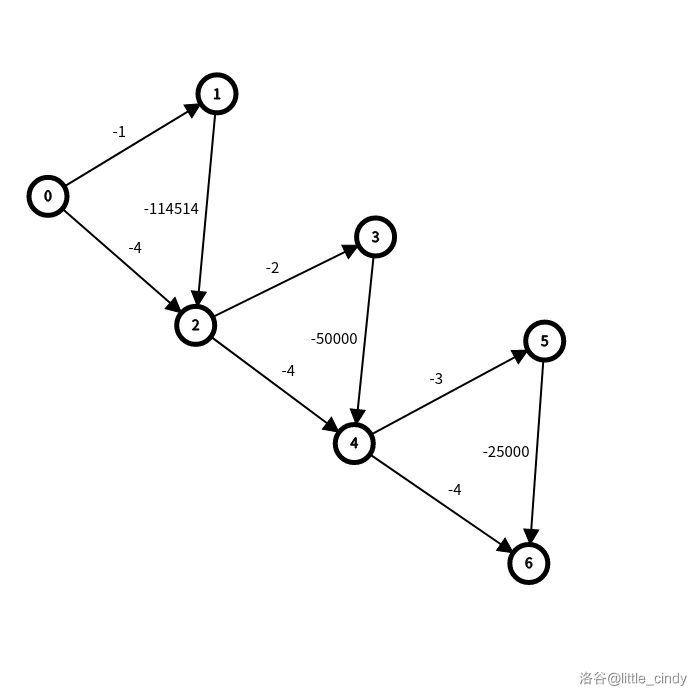
那么整个算法会按如下步骤进行:
| 当前点 | 当前操作 | 当前队列 |
|---|---|---|
| \(0\) | \(pop(0),push(1),push(2)\) | \(\{2,1\}\) |
| \(2\) | \(pop(2),push(3),push(4)\) | \(\{4,3,1\}\) |
| \(4\) | \(pop(4),push(5),push(6)\) | \(\{6,5,3,1\}\) |
| \(6\) | \(pop(6)\) | \(\{5,3,1\}\) |
| \(5\) | \(pop(5),push(6)\) | \(\{6,3,1\}\) |
| \(6\) | \(pop(6)\) | \(\{3,1\}\) |
| \(3\) | \(pop(3),push(4)\) | \(\{4,1\}\) |
| \(4\) | \(pop(4),push(5),push(6)\) | \(\{6,5,1\}\) |
| \(6\) | \(pop(6)\) | \(\{5,1\}\) |
| \(5\) | \(pop(5),push(6)\) | \(\{6,1\}\) |
| \(6\) | \(pop(6)\) | \(\{1\}\) |
| \(1\) | \(pop(1),push(2)\) | \(\{2\}\) |
| \(2\) | \(pop(2),push(3),push(4)\) | \(\{4\}\) |
| \(4\) | \(pop(4),push(5),push(6)\) | \(\{6,5\}\) |
| \(6\) | \(pop(6)\) | \(\{5\}\) |
| \(5\) | \(pop(5),push(6)\) | \(\{6\}\) |
| \(6\) | \(pop(6)\) | \(\text{empty}\) |
而发现节点 \(V\) 外每一个节点都拥有这个性质,所以时间复杂度为 \(\Theta(2^{\frac{V-1}{2}})\),忽略常数相当于 \(\Theta(2^V)\)。
证毕。
所以对于这道题,构造一组 \(V=33,Q=10\) 的数据即可
code
#include<bits/stdc++.h>
using namespace std;
const int maxv=305,maxq=15;
int V,E,Q;
vector<pair<int,int>> G[maxv];
int s[maxq],t[maxq];
int main(){
V=33;
int dis=200000;
for(int i=0;i<V;i++){
if(i==V-1){
continue;
}
if(i&1){
dis/=2;
G[i].push_back(make_pair(i+1,-dis));
}
else{
G[i].push_back(make_pair(i+1,-1));
G[i].push_back(make_pair(i+2,-2));
}
}
Q=10;
for(int i=1;i<=Q;i++){
s[i]=0;
t[i]=32;
}
print();
return 0;
}
point 5
目的
卡掉 \(\text{Bellman-Ford}(\Theta(VEQ))\)
且需要让 \(\text{Dijkstra}(\Theta(QE+Q\log_2 E))\) 过
做法
同 point 2,我们需要在一条链上狂加自环。
另外我们发现其实 \(\text{Dijkstra}\) 的时间复杂度是不会受 \(V\) 的影响的,然后我们就让 \(V\) 尽量大,也就是 \(V=300\),\(Q\) 也设为 \(10\)。
简单计算发现 \(E_{\max}=\frac{1016-1(V)-300(出度)-1(Q)-2\times10(询问)}{2}-299(链)=48\)
code
#include<bits/stdc++.h>
using namespace std;
const int maxv=305,maxq=15;
int V,E,Q;
vector<pair<int,int>> G[maxv];
int s[maxq],t[maxq];
int main(){
V=300;
E=48;
for(int i=0;i<V;i++){
int k=min(E,10);
E-=k;
if(i!=0){
G[i].push_back(make_pair(i-1,rand()%114514+114514));
}
for(int j=1;j<=k;j++){
G[i].push_back(make_pair(i,rand()%114514+114514));
}
}
Q=10;
for(int i=1;i<=Q;i++){
s[i]=299;
t[i]=0;
}
print();
return 0;
}
point 6
同 point 4,只是 \(Q\) 过大导致超出限制,\(Q\) 改为 \(6\) 即可。
point 7
目的
卡掉 \(\text{Backtrack}\),让 \(\text{Gamble1}\) 过。
做法
首先明确一点,这个 \(\text{Gamble1}\) 是个永远不会被卡掉的程序,所以你只需要管 \(\text{Backtrack}\)。
而你其实可以很显然的发现 \(\text{Backtrack}\) 的时间复杂度大无比,所以可以直接随机一组数据。
点数是随意的,而 \(E_{\max}=\frac{3004-1(V)-1(E)}{2}=1501\)。
所以我们让 \(V=999,E=1501\)。
code
#include<bits/stdc++.h>
using namespace std;
const int maxv=1005;
int V,E;
bool G[maxv][maxv];
vector<pair<int,int>> e;
int main(){
V=999;
E=1501;
for(int i=1;i<=E;i++){
int x=rand()%V;
int y=rand()%V;
while(G[x][y]||G[y][x]||x==y){
x=rand()%V;
y=rand()%V;
}
G[x][y]=G[y][x]=1;
e.push_back(make_pair(x,y));
}
reverse(e.begin(),e.end());
print();
return 0;
}
point 8
目的
卡掉 \(\text{Gamble2}\) ,\(\text{Backtrack}\) 让过。
做法
首先明确以下, \(\text{Gamble2}\) 是一个永远都过不去的算法,所以不用管。
而这个 \(\text{Backtrack}\) 是暴力染色,所以我们良心一点,让它能够一遍染完。
所以我们再造数据的时候先提前染好色,这样就能过了。
注意这里 \(V\) 不能过大,否则会把 \(\text{Backtrack}\) 卡掉。
code
#include<bits/stdc++.h>
using namespace std;
const int maxv=1005;
int V,E;
int col[maxv];
bool G[maxv][maxv];
vector<pair<int,int>> e;
int main(){
V=101;
E=1501;
for(int i=1;i<=V;i++){
col[i]=rand()%2;
}
for(int i=1;i<=E;i++){
int x=rand()%V;
int y=rand()%V;
while(col[x]==col[y]||G[x][y]||G[y][x]||x==y){
x=rand()%V;
y=rand()%V;
}
G[x][y]=G[y][x]=1;
e.push_back(make_pair(x,y));
}
reverse(e.begin(),e.end());
print();
return 0;
}
完结撒花!
后记
这篇题解我是边写题边写的
一共提交 \(26\) 次才获得 AC
下面是通过各个测试点的时间:
| 测试点编号 | 时间 | 失败次数 |
|---|---|---|
| \(1\) | \(\texttt{2022-07-27 10:22:54}\) | \(0\) |
| \(2\) | \(\texttt{2022-07-27 11:16:21}\) | \(0\) |
| \(3\) | \(\texttt{2022-07-27 11:14:03}\) | \(0\) |
| \(4\) | \(\texttt{2022-07-27 12:25:53}\) | \(10\) |
| \(5\) | \(\texttt{2022-07-27 14:12:41}\) | \(0\) |
| \(6\) | \(\texttt{2022-07-27 14:18:34}\) | \(3\) |
| \(7\) | \(\texttt{2022-07-27 14:37:29}\) | \(1\) |
| \(8\) | \(\texttt{2022-07-27 14:51:48}\) | \(4\) |
历时共 \(16134\text{s}\),合计 \(268.9\text{min}\),相当于约 \(4.18167\text{h}\)。
全文共 \(11664\) 个字。
码字不易,点个赞再走吧~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号