利用母函数求递推关系的递推通项(解递推关系)
利用母函数求递推关系的递推通项(解递推关系)
一、预备
1.0 阅读书本P43 - P46
1.1 母函数的定义

1.2 递推关系
n层河内塔移动次数 等于 第n-1层河内塔次数两倍+1
例如:移动2层河内塔移动次数是1层河内塔移动次数的两倍+1
1*2+1=3
所以移动2层河内塔的移动次数是3。移动3层河内塔的移动次数3*2+1=7 ……
1.3 递推通项
上面的等式叫做递推关系。我们要求H(n)就必须要知道H(n-1),要求H(n-1)就必须要知道H(n-2)……
我们能不能找到一个式子不用求前面的项就能知道H(n)的值?这就是我们的目标!
二、 河内塔问题
利用母函数求递推关系的递推通项,这个方法如下图所示。

2.1 已知河内塔的递推关系H(n)=2H(n-1)+1, H(1)=1
2.2 构造母函数
当知道一个递推关系时,我们就可以利用递推关系生成一个序列。汉诺塔的递推序列{Hn}为:
{1,3,7,15,31,63,……}

2.3 ※求母函数(变化最多,最复杂,计算量最大的一步)
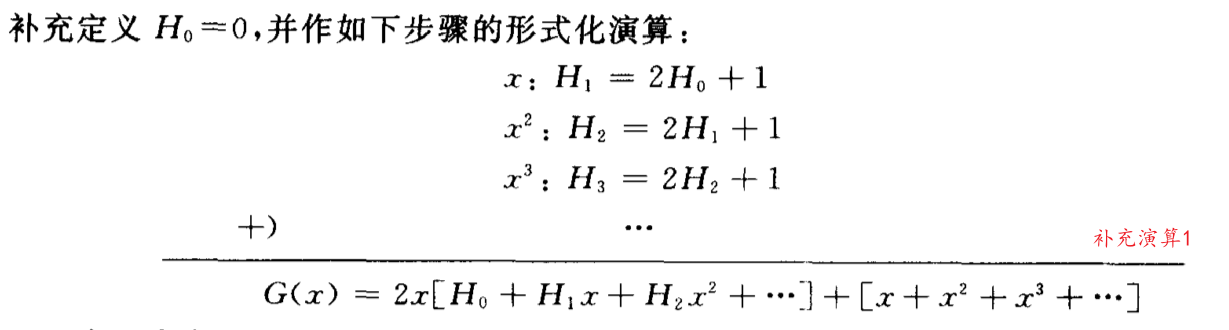
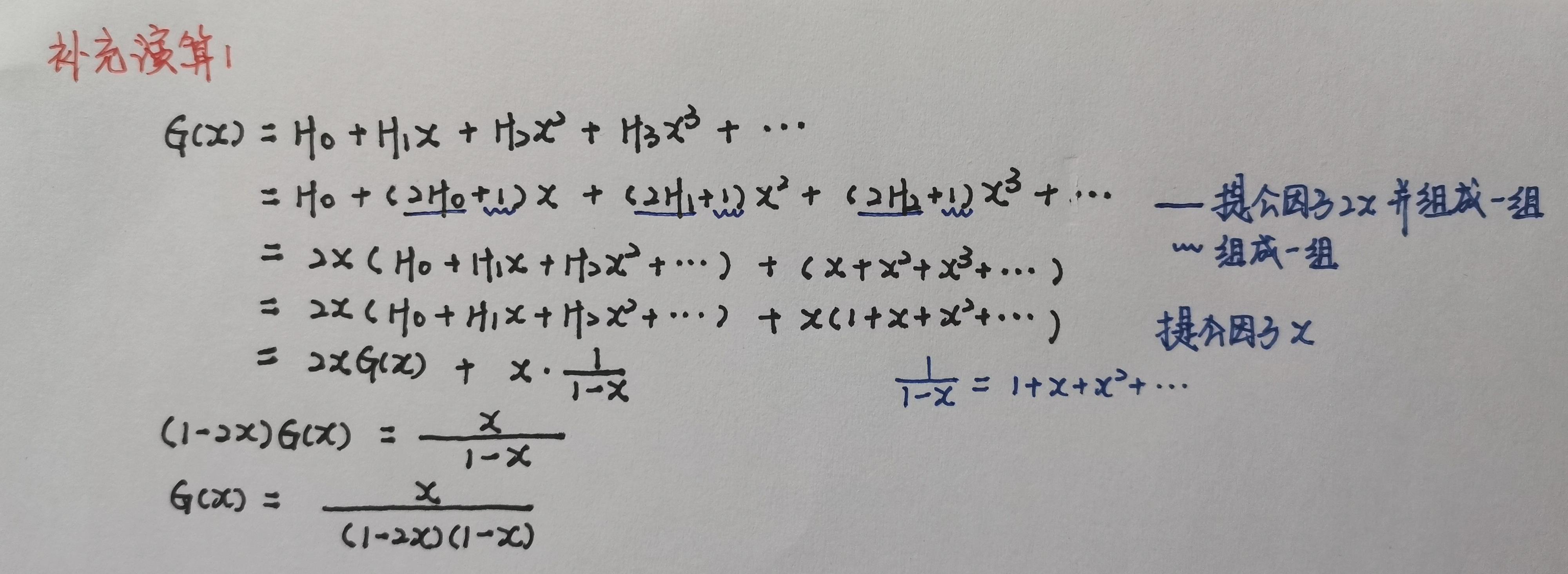
求得序列{Hn}的母函数:
2.4 求递推通项


三、 Fibonacci序列(斐波那契序列)
3.1 已知Fibonacci序列的递推关系

3.2 构造母函数
3.3 求母函数


3.4 求递推通项

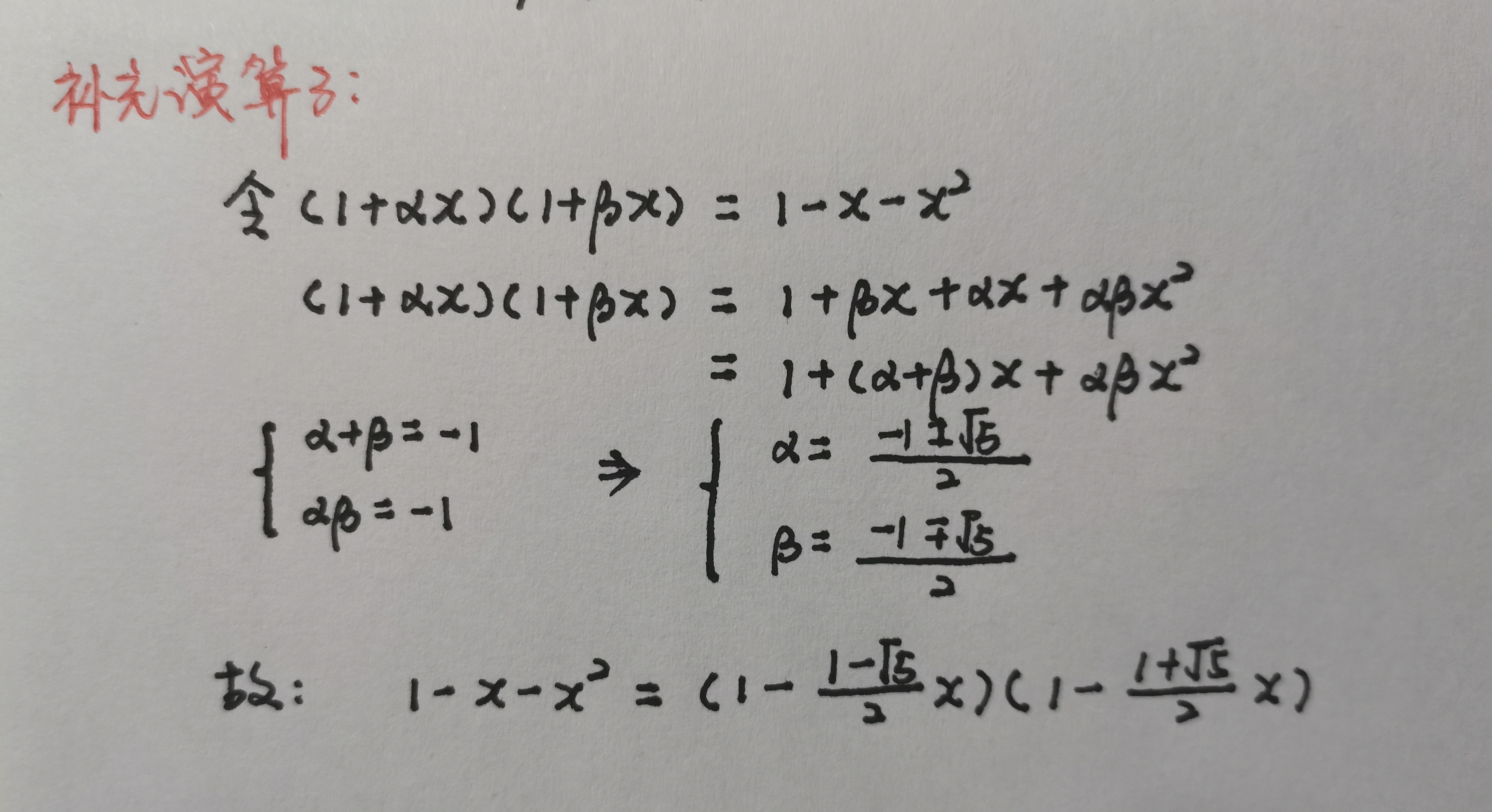



 浙公网安备 33010602011771号
浙公网安备 33010602011771号