含量和分量的重新理解

在神经网络结构的学习中，乘加结构是基础，乘法是含量的计算，加法是分量的计算。

计算总和，则自然直观的把每个分量乘以权重（含量的百分比），再把这每个结果（分量）逐个加起来，得到一个整体。

如图：

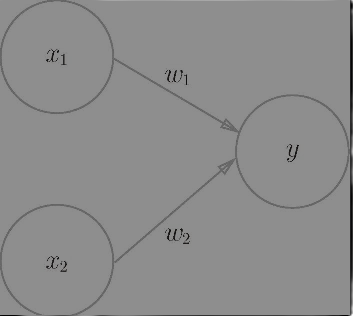
上图中，y是结果，y 由 x1 和 x2 两个分量组成，x1的有效成分占比是权重 w1 表示，x2 的有效成分占比是权重 w2 表示，这样 y 的总共有效成分为 y = x1 * w1 + x2 * w2 构成。

这种计算既符合直观的，自然的理解，也符合哲学“层级”结构的要求，即简洁又深奥。

链式法则

同理，在上图链式法则的求导公式中，我看到了同样的“含量，分量”结构。

在函数 f(x(t),y(t)) 中 变量 t 就是最终物质，它被包含在两个分量 x(t) 和 y(t) 中，那么针对求解函数 f 相对于 t 的变换率，则

(df / dt) = (∂f / ∂x) * (dx / dt) + (∂f / ∂y) * (dy / dt)

注意 ∂ 代表偏导，d 代表单变量导数。

总结

乘法对应着含量，对于的是 某物质的重量 / 整体重量 的一种百分比表示。

加法对于分量，是某物质的重量，是一种单纯的量的表示。

在上面的链式法则中，x(t) 和 y(t) 代表了不同的维度，它们之间是互不干涉的关系。

附

链式法则在多变量中的情况。单变量链式法则很简单，但多变量的话，可能需要用矩阵乘法或者组合偏导数。

比如，如果有函数f(x,y)，而x和y又是t的函数，那么df/dt就是∂f/∂x * dx/dt + ∂f/∂y * dy/dt，这就是链式法则了。

如果是更复杂的情况，比如函数有多个变量，中间变量又是其他变量的函数，那么链式法则需要更仔细的应用。

比如，f(u,v), u=u(x,y), v=v(x,y)，那么∂f/∂x = ∂f/∂u * ∂u/∂x + ∂f/∂v * ∂v/∂x，这个时候每个中间变量都要考虑进去，乘积然后相加。