查找算法浅显探究
在考研复习的过程中,数据结构复习到了查找这一章节,学习了各种各样的查找算法,为了不至于过于凌乱,现将它进行总结:
- 顺序查找
- 折半查找
- 分块查找
- 二叉搜索树
- B树
- B+树
- 散列查找
一、顺序查找
思路:按照顺序从前往后或者从后往前找,通常会设置一个哨兵防止越界
优点:顺序查找的算法简单、对存储结构没有要求,且对关键字的次序也无要求
缺点:效率过低。
代码:
/*在顺序表str[0…n-1]中查找关键字为k的记录 */
int SeqSearch(int str[],int n,int k)
{
int i=0;
str[n]=k; //设置哨兵,防止越界
while(str[i]!=k) i++;
if (i<n) return i+1;
else return -1;
}
二、折半查找
思路:迭代的思想,每次与待查数组的中间值【(low+high)/2】进行对比
优点:算法简单、在某些情况下效率较高
缺点:只适应于有序的顺序表(需要实现随机访问),当数据被查概率不同时,折半查找的效率不一定优于顺序查找。
代码:
int Search_Bin(SSTable *ST,keyType key){
int low=1; //初始状态 low 指针指向第一个关键字
int high=ST->length; //high 指向最后一个关键字
int mid;
while (low<=high) {
mid=(low+high)/2; //int 本身为整形,所以,mid 每次为取整的整数
if (ST->elem[mid].key==key) //如果 mid 指向的同要查找的相等,返回 mid 所指向的位置
return mid;
else if(ST->elem[mid].key>key) //如果mid指向的关键字较大,则更新 high 指针的位置
high=mid-1;
//反之,则更新 low 指针的位置
else low=mid+1;
}
return 0;
}
三、分块查找
引入:一般对于需要查找的待查数据元素列表来说,如果很少变化或者几乎不变,则我们完全可以通过排序把这个列表排好序以便我们以后查找。但是对于经常增加数据元素的列表来说,要是每次增加数据都排序的话,那真的是有点太累人了。对于几乎不变的数据列表来说,排序之后使用二分查找是很不错的,但是对于经常变动的数据元素列表来说,每次排序后再使用二分查找则不是很好的选择。在这种情况下可以采用分块查找
思路:分块查找是结合二分查找和顺序查找的一种改进方法。在分块查找里有索引表和分块的概念。索引表就是帮助分块查找的一个分块依据,其实就是一个数组,用来存储每块的最大存储值,也就是范围上限;分块就是通过索引表把数据分为几块
优点:算法简单,在数据经常变动的表中也有较好的效果。有顺序的优势,二分的速度
缺点:分块的大小对算法的效率有很大的影响。
代码:在实际中一般不会用到分块查找,一般是分块的思想。比如学校组织考试,班内打乱顺序,班级之间有序
四、二叉搜索树(二叉排序树)
若它的左子树不为空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不为空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树分别为二叉排序树。
这样的树称为二叉排序树,用于搜索时也叫二叉搜索树。
特点:左<根<右
查找思路:
若和根节点值相同,则返回根节点值;若比根节点小,就递归查找左子树,若比根节点大,则递归查找右子树。
代码:
BSTNode * BST_Search(BiTree T, Type key) while( T != NULL && key != T->data) if(key < T->data) T = T->Lchild; else T = T->Rchild; return T;
五、B树
B树是一颗满足特殊要求的m叉树,其比较重要的要求为
- 根结点且不是叶子结点,则至少要有两个分支,非根非叶结点至少有ceil(m/2)个分支,这里ceil代表向上取整。
- 结点内各关键字互不相等且按从小到大排列
- 叶子结点处于同一层

如图,为5叉树,则分支结点至少要ceil(m/2)=5/2+1=3个分支,即至少2个节点。
思路:B-树的查找很简单,是二叉排序树的扩展,二叉排序树是二路查找,如果key不等于结点,则找到第一个大于它的结点进入左边,如果找不到,则走右边
应用场景:应用在磁盘组织上,如大型数据库文件存储在硬盘上
优化:B+树
六、B+树
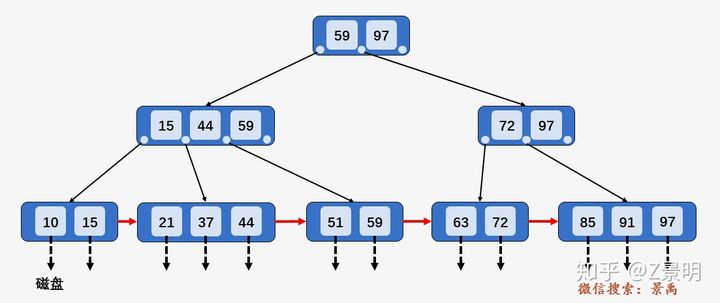
每个key没有右指针,有效数据结点全都保存在叶子结点,分支结点的指针充当索引的作用,分支结点的key值一定在叶子结点出现。
七、散列查找
思路:根据散列函数确定位置,如果不相同则应用冲突办法解决冲突
实质:用一个函数f(x),实现直接由key值到地址的映射。
散列函数:
- 直接定址法:线性方程y=ax+b;
- 除模取余法:y=x mod c
- 平方取中法:y= x*x只取中间几位
- 数字分析法:y=找比较随机的位置的数据
冲突解决办法:
- 开放地址法
- 线性探测,冲突了就一个一个往后找空位
- 平方探测,按照i*i, -i*i的规律找探测位
- 多散列:再用一个散列函数散列
- 拉链法
- 没冲突的好好放,冲突的在后边拉一条链表



 浙公网安备 33010602011771号
浙公网安备 33010602011771号