P4139（扩展欧拉定理的应用）

欧拉定理及扩展

题意：求

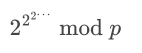
思路：

运用扩展欧拉定理进行欧拉降幂：

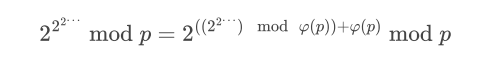
然后递归求解即可。

AC代码：

// -----------------
//#pragma GCC optimize(2)
#include <iostream>
#include <cstring>
#include <algorithm>
#define IOS ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(0);
#define fixed fixed<<setprecision
#define endl '\n'
#define int long long 
using namespace std;

const int N = 1e7 + 7;

int mod, p;
int primes[N], cnt, phi[N];
bool st[N];

int qmi(int a, int k, int p) 
{
    int res = 1 % p;
    while (k)
    {
        if (k & 1) res = res * a % p;
        a = a * a % p;
        k >>= 1;
    }
    return res;
}

void init(int n)  // 预处理欧拉函数
{
    phi[1] = 1;
    for(int i = 2; i <= n; i ++)
    {
        if(!st[i]) primes[ ++cnt] = i,phi[i] = i - 1;
        for(int j = 1; j <= cnt && i * primes[j] <= n; j ++)
        {
            st[i * primes[j]] = true;
            if(i % primes[j] == 0)
            {
                phi[i * primes[j]] = phi[i] * primes[j];
                break;
            }
            phi[i * primes[j]] = phi[i] * (primes[j] - 1);
        }
    }
}

int dfs(int a, int p)  // 递归求解
{
    if(p == 1) return 0;
    return qmi(a, dfs(a, phi[p]) + phi[p], p);
}

void solve()
{
    cin >> p;
    mod = p;
    int ans = dfs(2, p);
    cout << ans << endl;
}

signed main()
{
    IOS init(N - 7); 
    int T = 1;
    cin >> T;
    while(T --) { solve(); }
    return 0;
}