Transformer中的细节

1.Cross self attention

1. 第一个就是这个地方，我们将编码器的输出看成key和value,然后将第一个多头注意力层输出的值看成query.其实这里可以看成Cross Attention，而不是self Attention。Cross Attention会用解码器生成的q来查询编码器生成的k和v。一起计算attention score之后，softmax之后，将编码器的向量v按权相加。


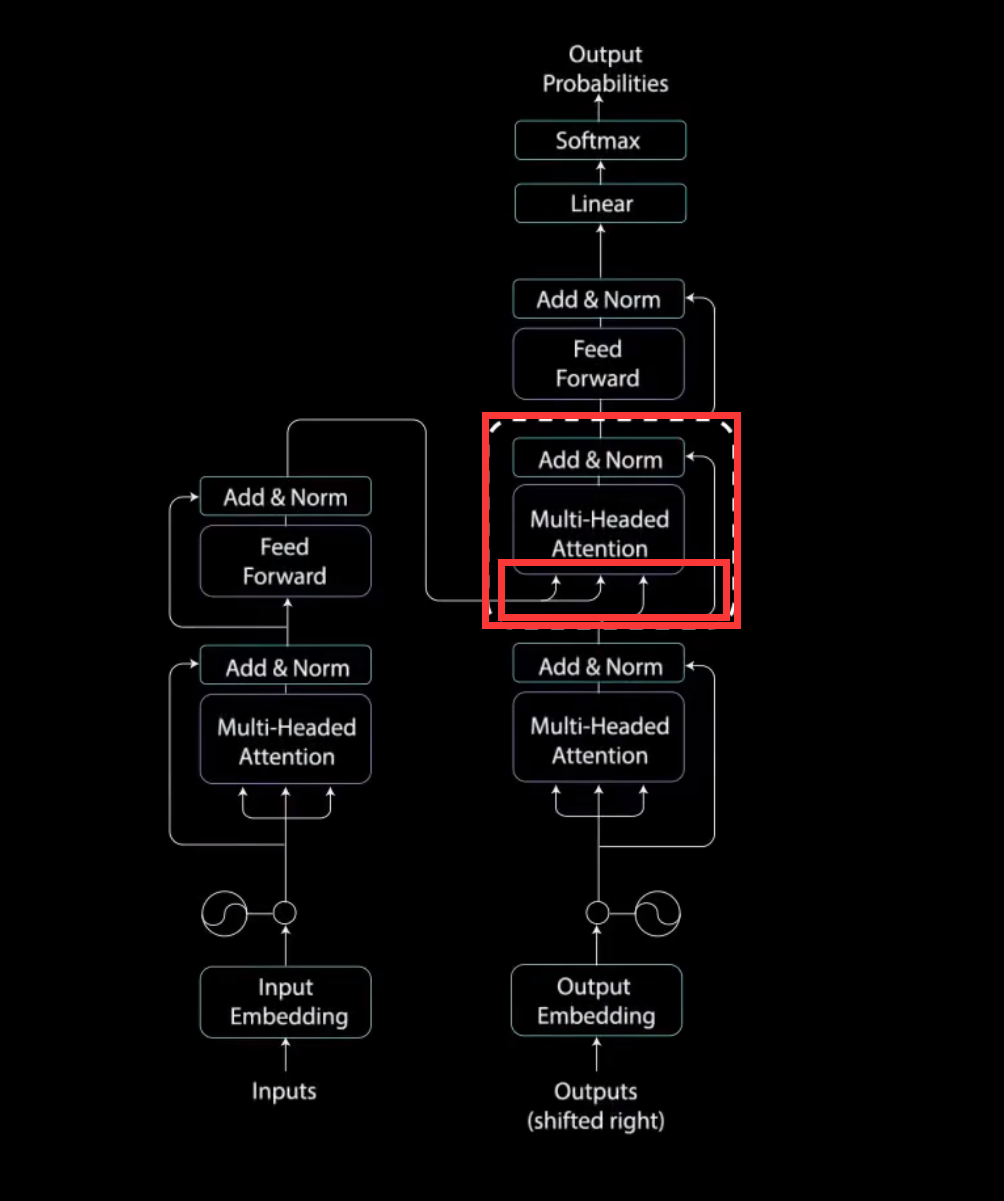
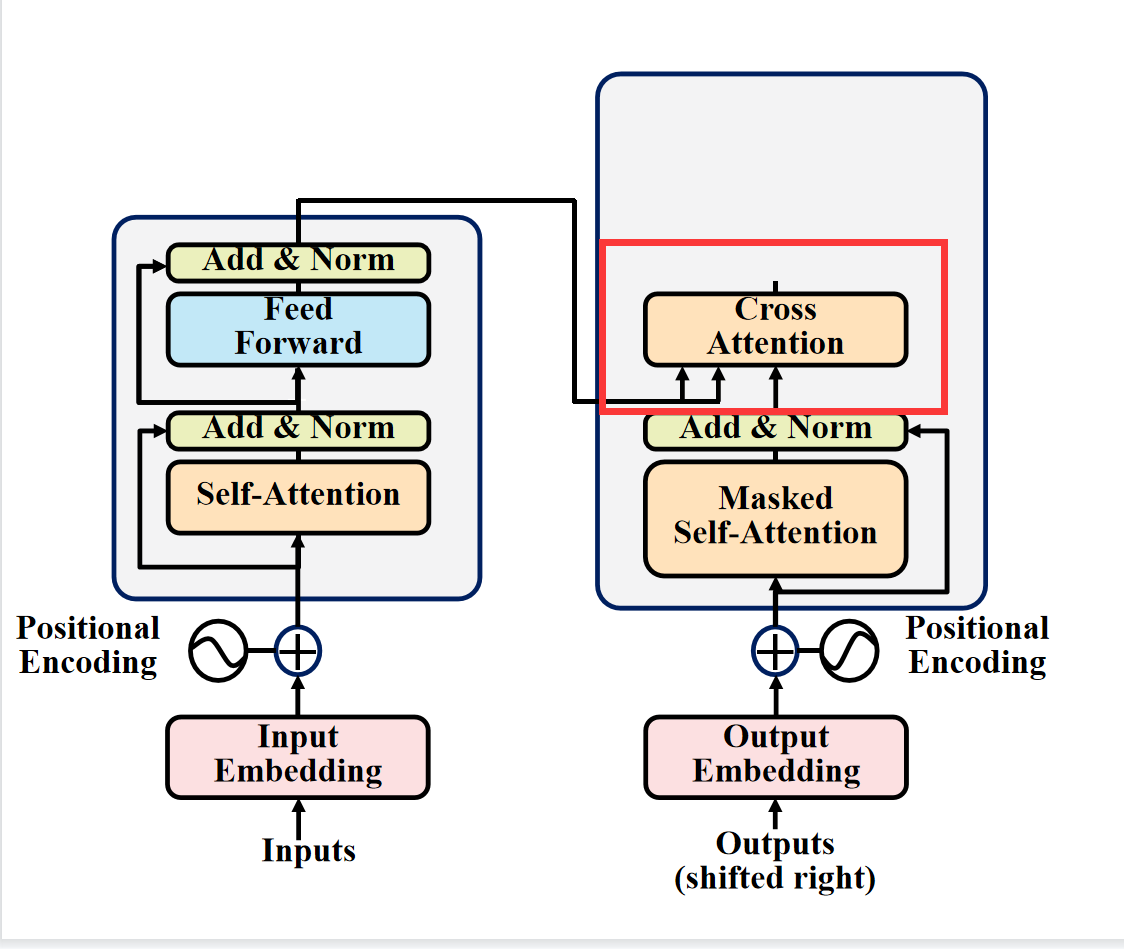
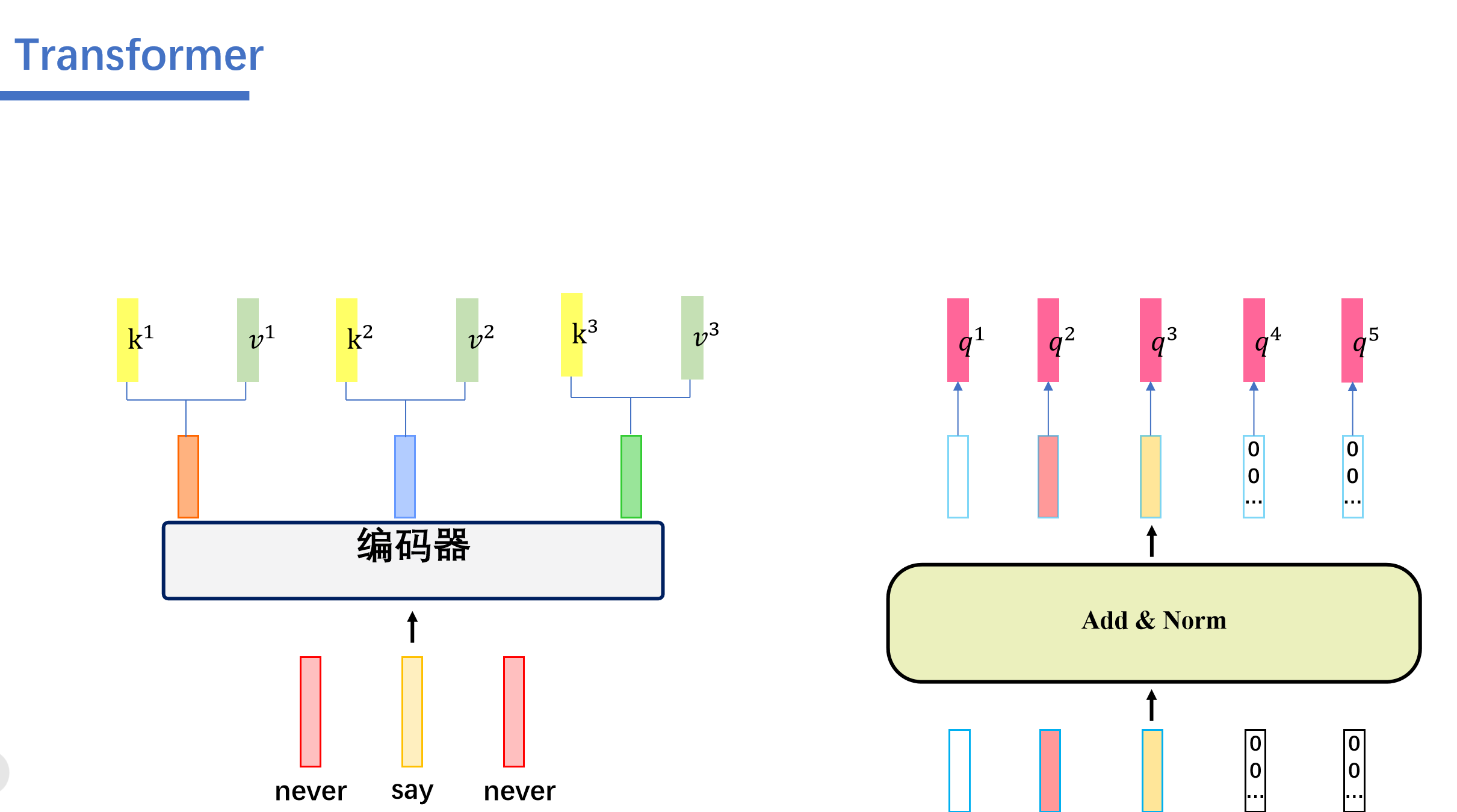
具体操作是这样的。
cross attention会用解码器生成q,然后Cross Attention会用解码器生成的q来查询编码器生成的k和v。一起计算attention score之后，softmax之后，将编码器的向量v按权相加。我们假设"never say never"通过编码器生成三个向量，接着解码器这边的5个向量，生成对应的q向量。然后编码器这边的三个向量会生成对应的k，v向量。

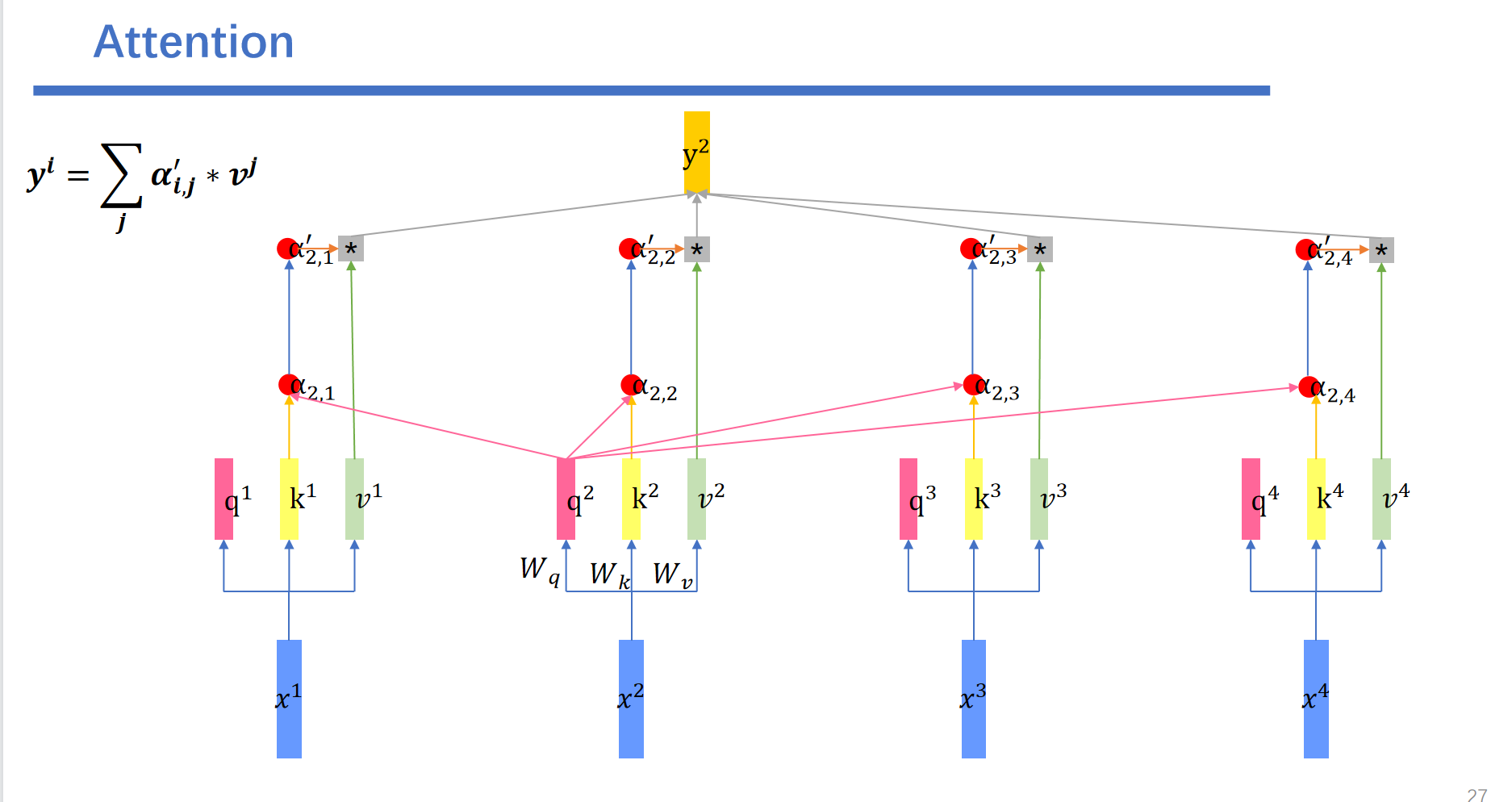
然后我们用解码器这个的q去查询编码器这边的k，也就是做一个内积的操作。得到attention score \(\alpha\)，之后这些\(\alpha\)再softmax得到对应的\(\alpha^{'}\)。与对应的v相乘后相加。即可得到我们的输出\(y^1\)。

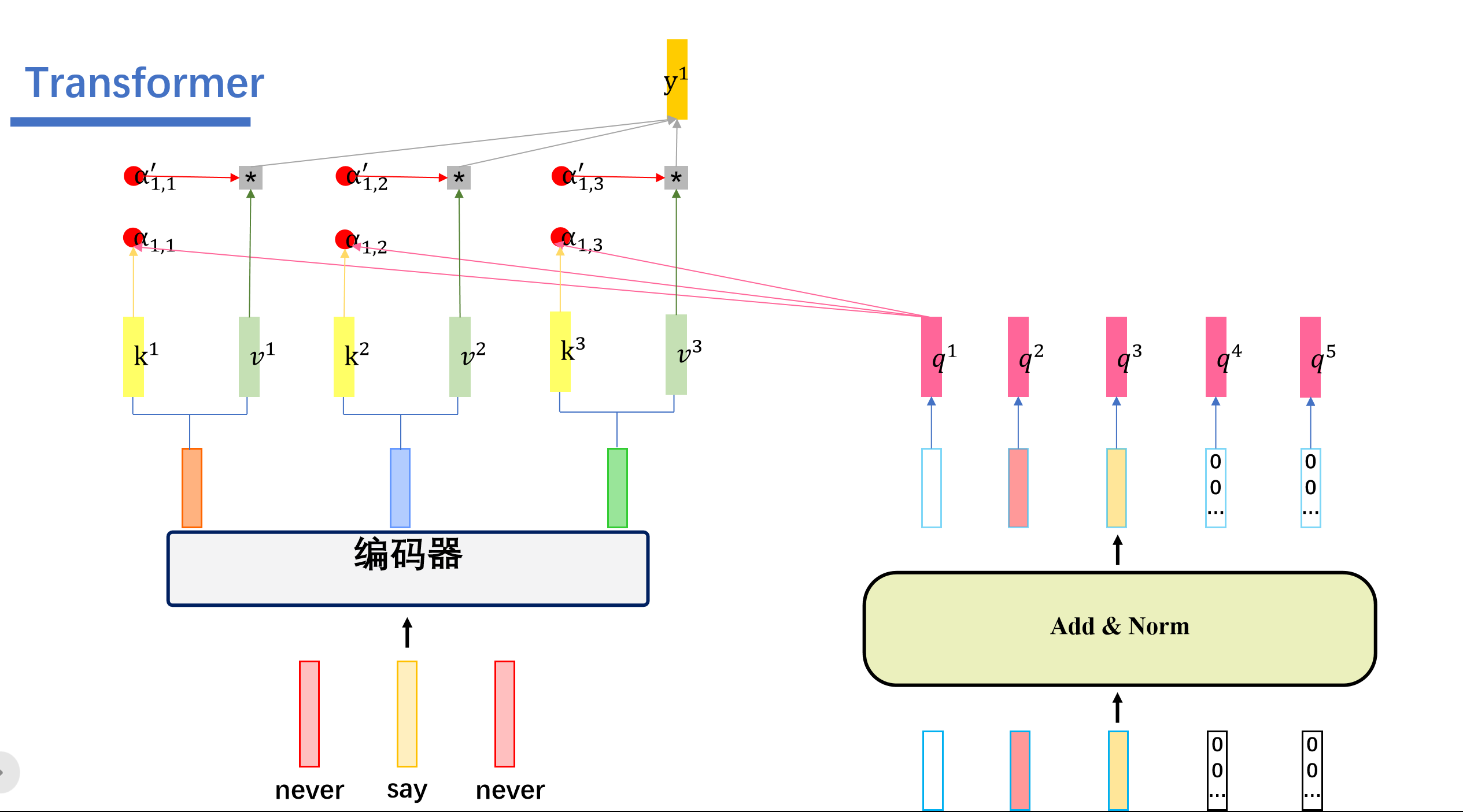
我们这里举的例子是用\(q^1\)查询得到的\(y^1\)，然后我们用\(q^2\)查询会得到\(y^2\)，用\(q^3\)查询会得到\(y^3\).....用\(q^5\)查询会得到\(y^5\)。
与传统的self attention一样，这里的cross attention也是输入多少矩阵输出多少矩阵。

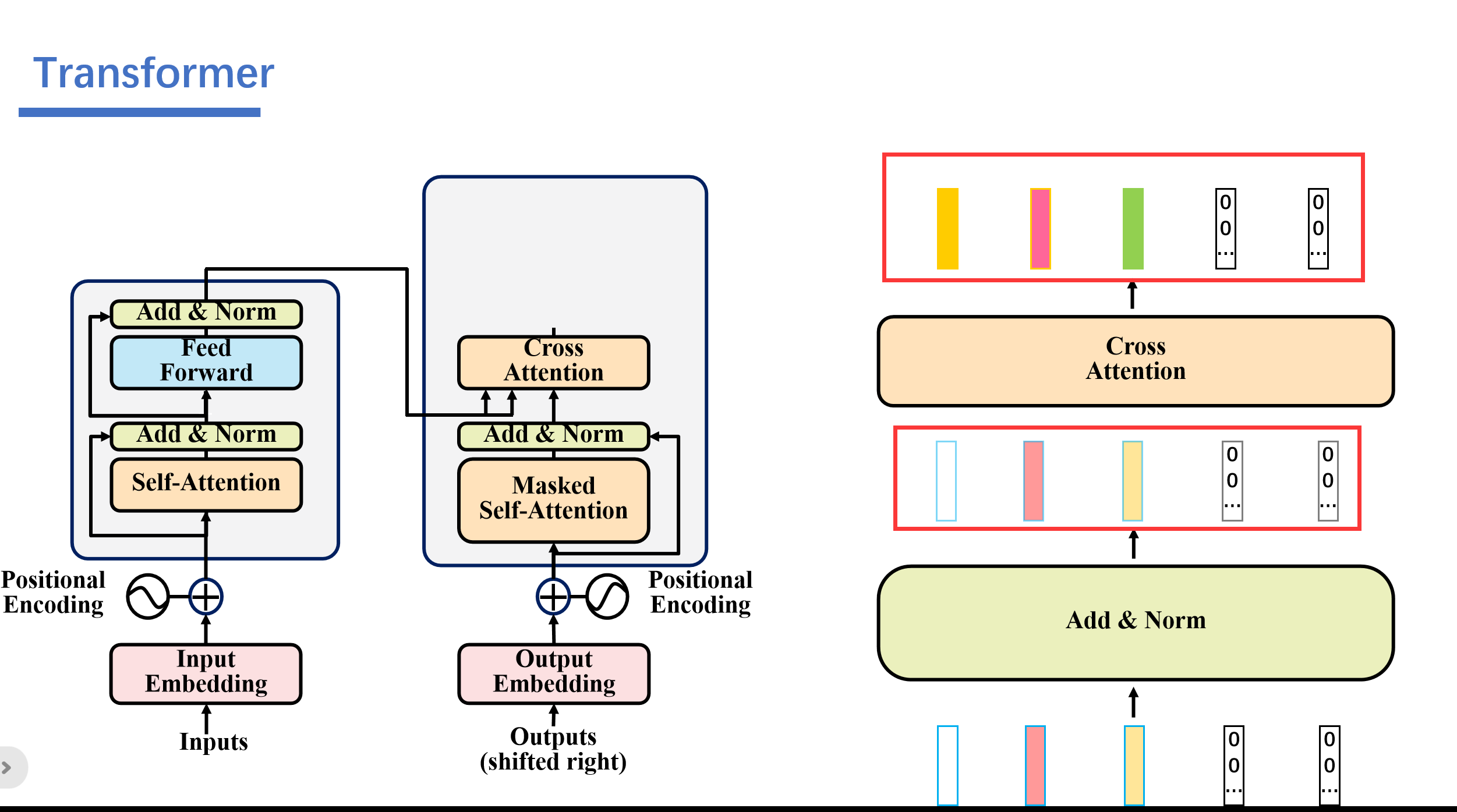
之后再经过Add&Norm和，Feed Forward，Add&Norm。

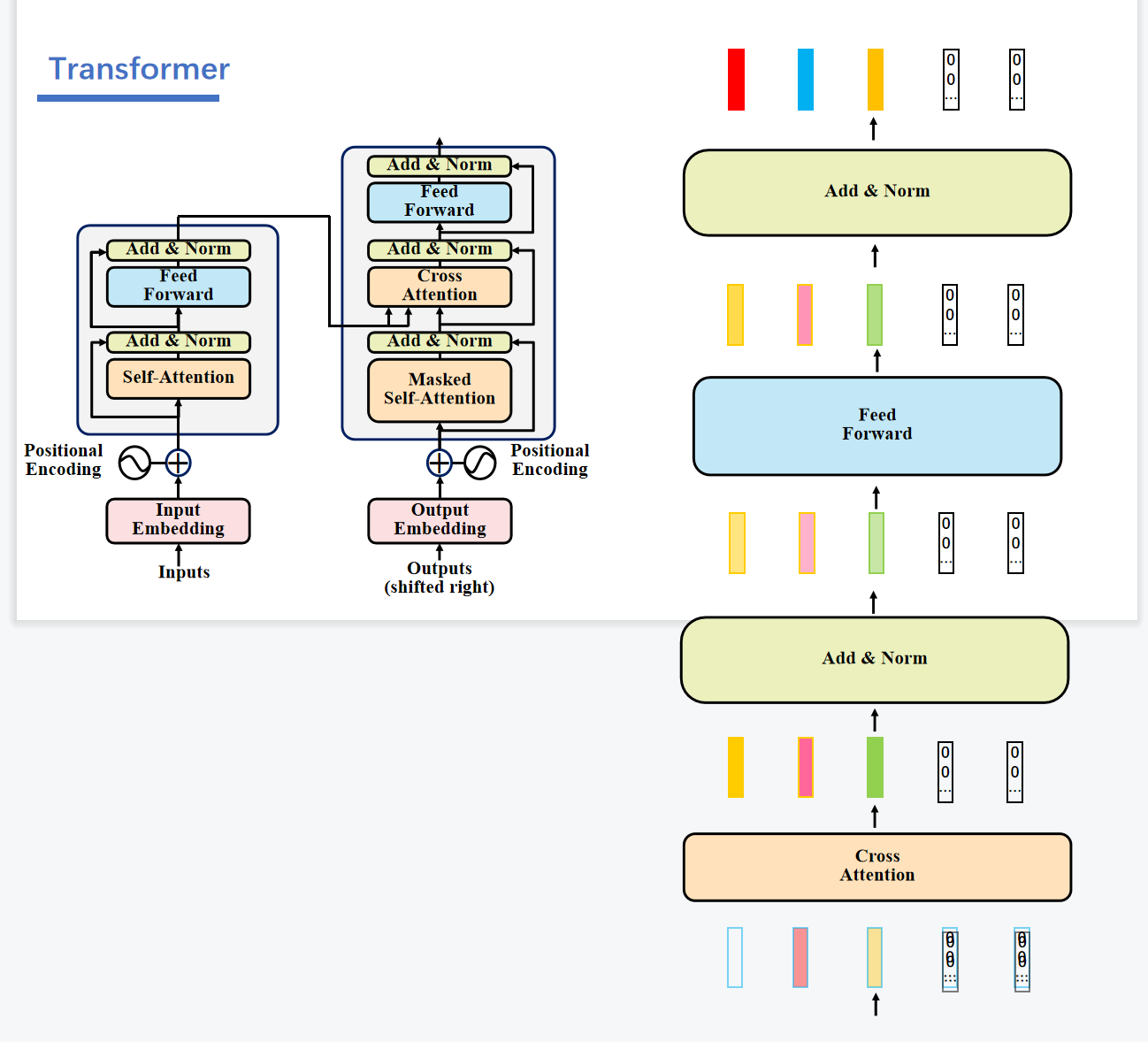
之后再经过线性层进行输出。

2.共享权重

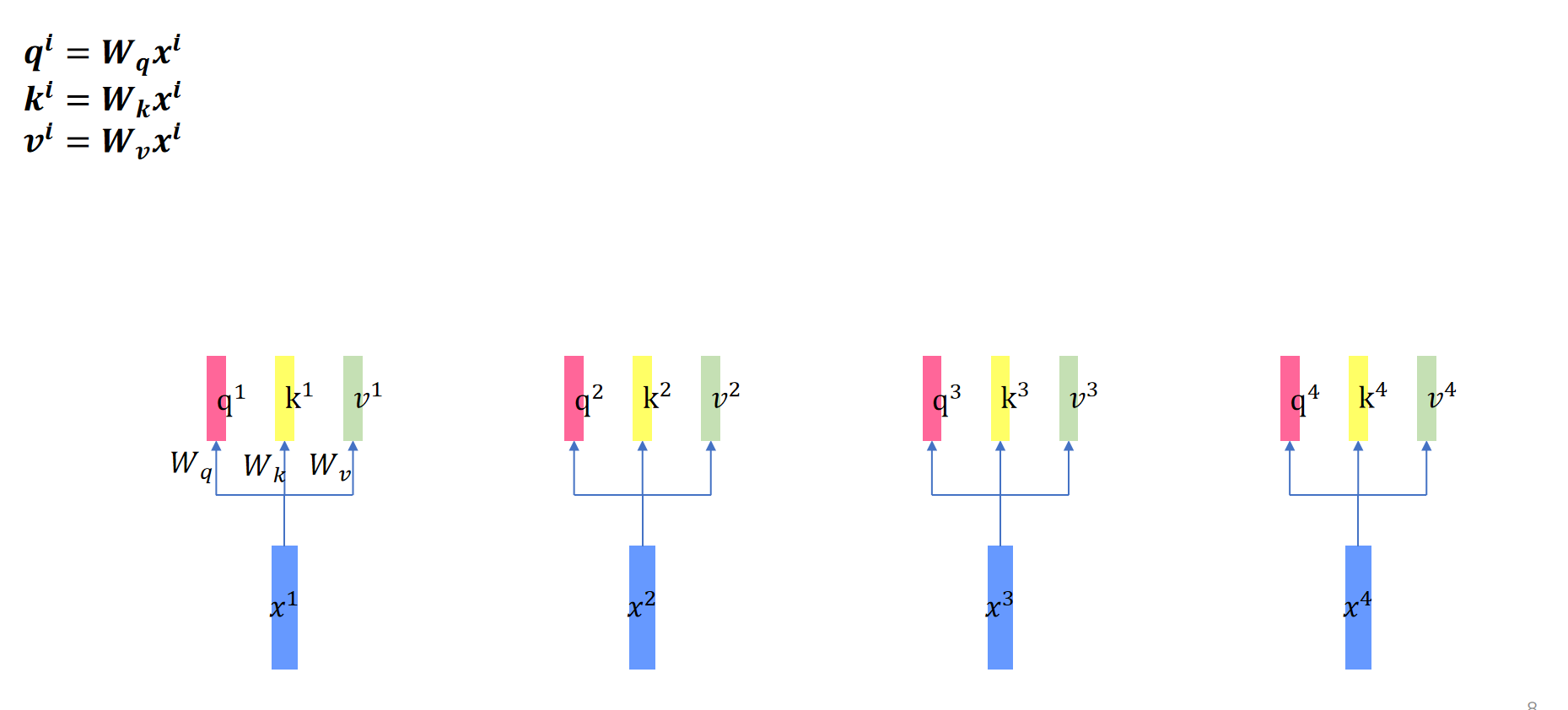
2. 再算self attention的时候\(W^k,W^q,W^v\)是共享权重的。
例如再算这里的时候\(x^1,x^2,x^3,x^4\)用的同一组参数\(W^k,W^q,W^v\)。

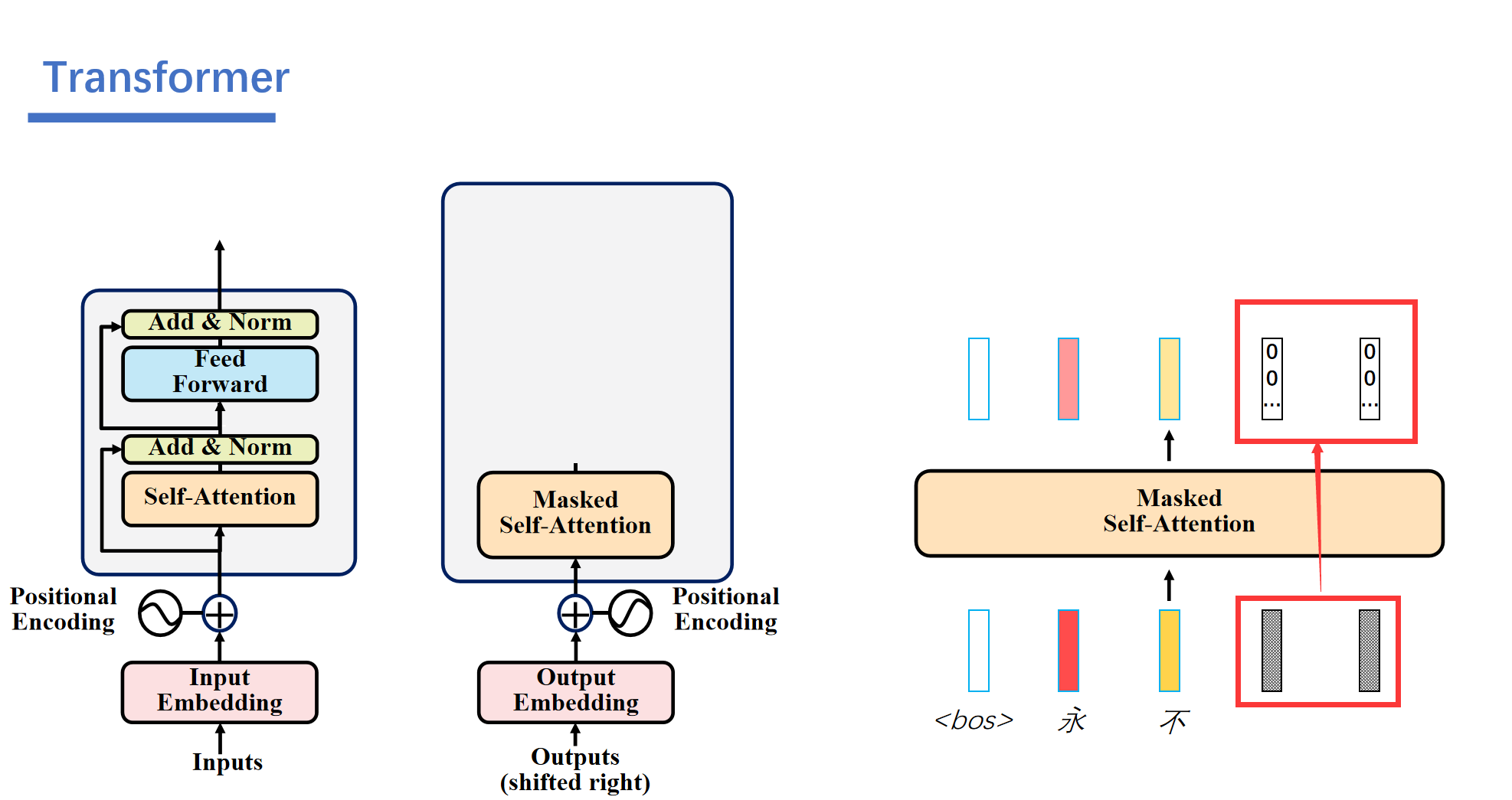
3. Masked Self-Attention
解码器是自回归的,比如说一开始我们只知道<bos>的，然后后面的我们都不知道，都是一些随机的数。

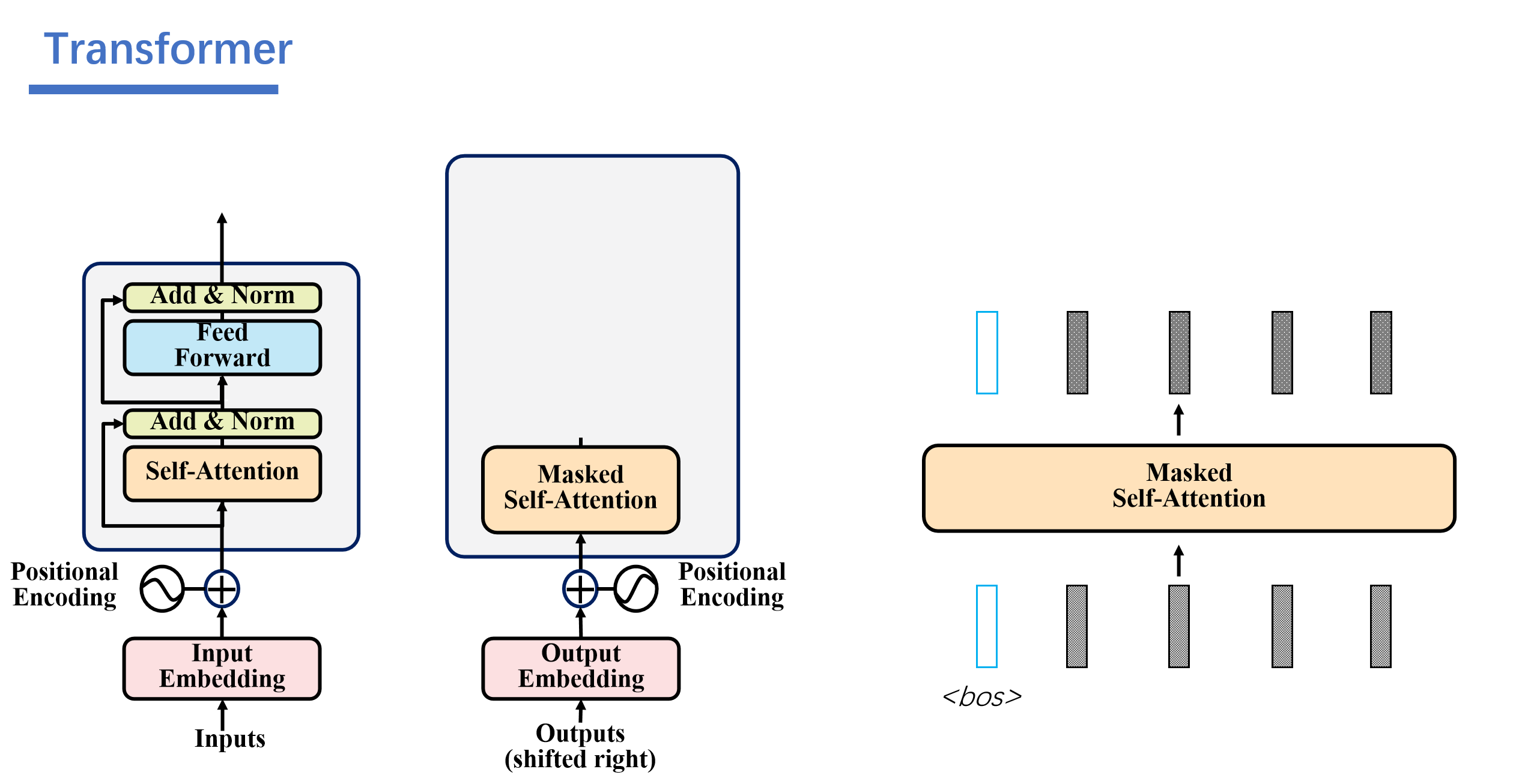
接着解码器就会根据编码器的信息和我们仅有的<bos>的信息，经过一顿运算之后就能输出结果"永"。

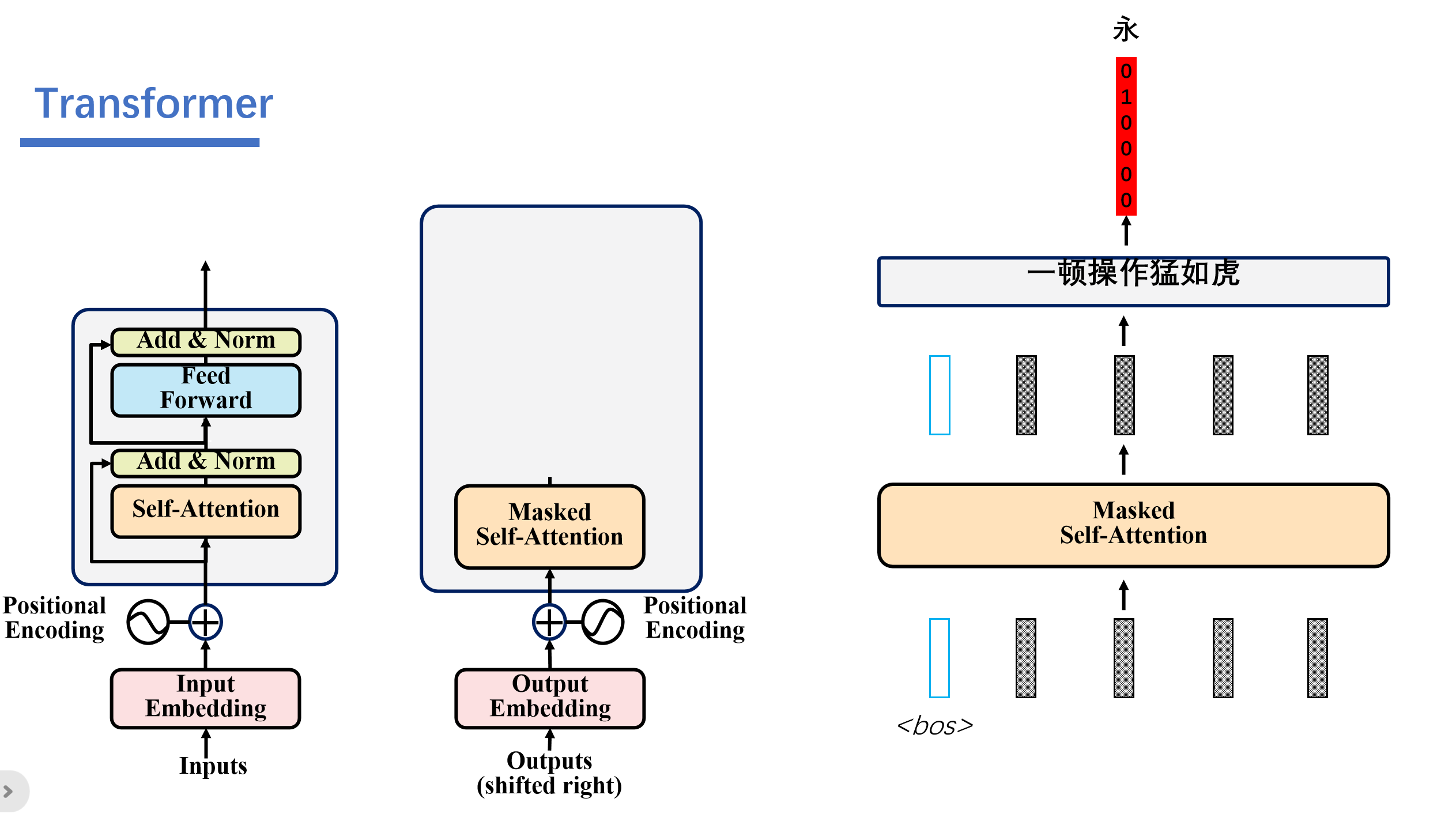
然后这个预测出来的永的信息会加入到编码器的输入中。然后解码器就可以结合编码器的信息和<bos>，永的信息，得到信息不。

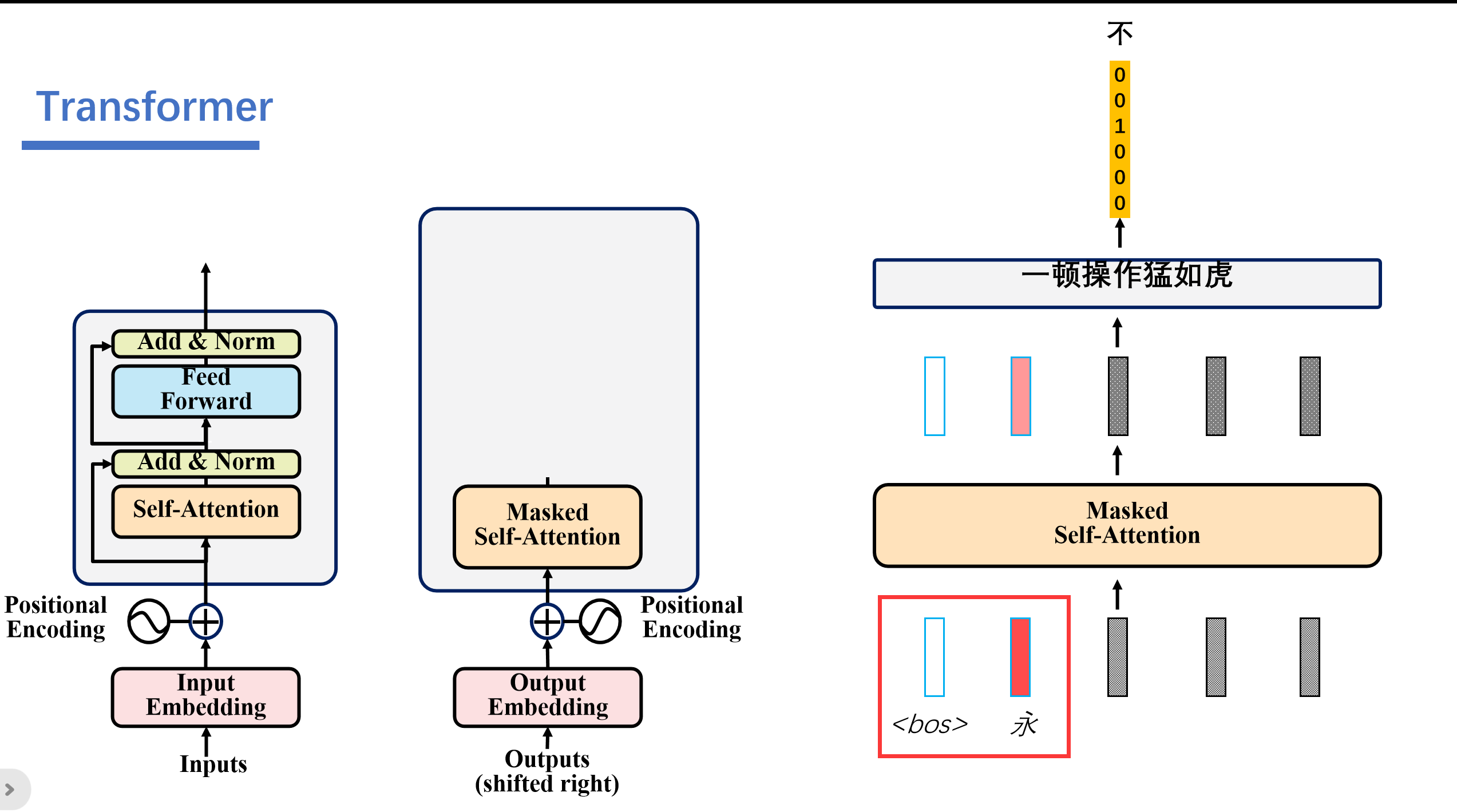
之后再根据<bos>,永,不的信息预测出来言。

.....
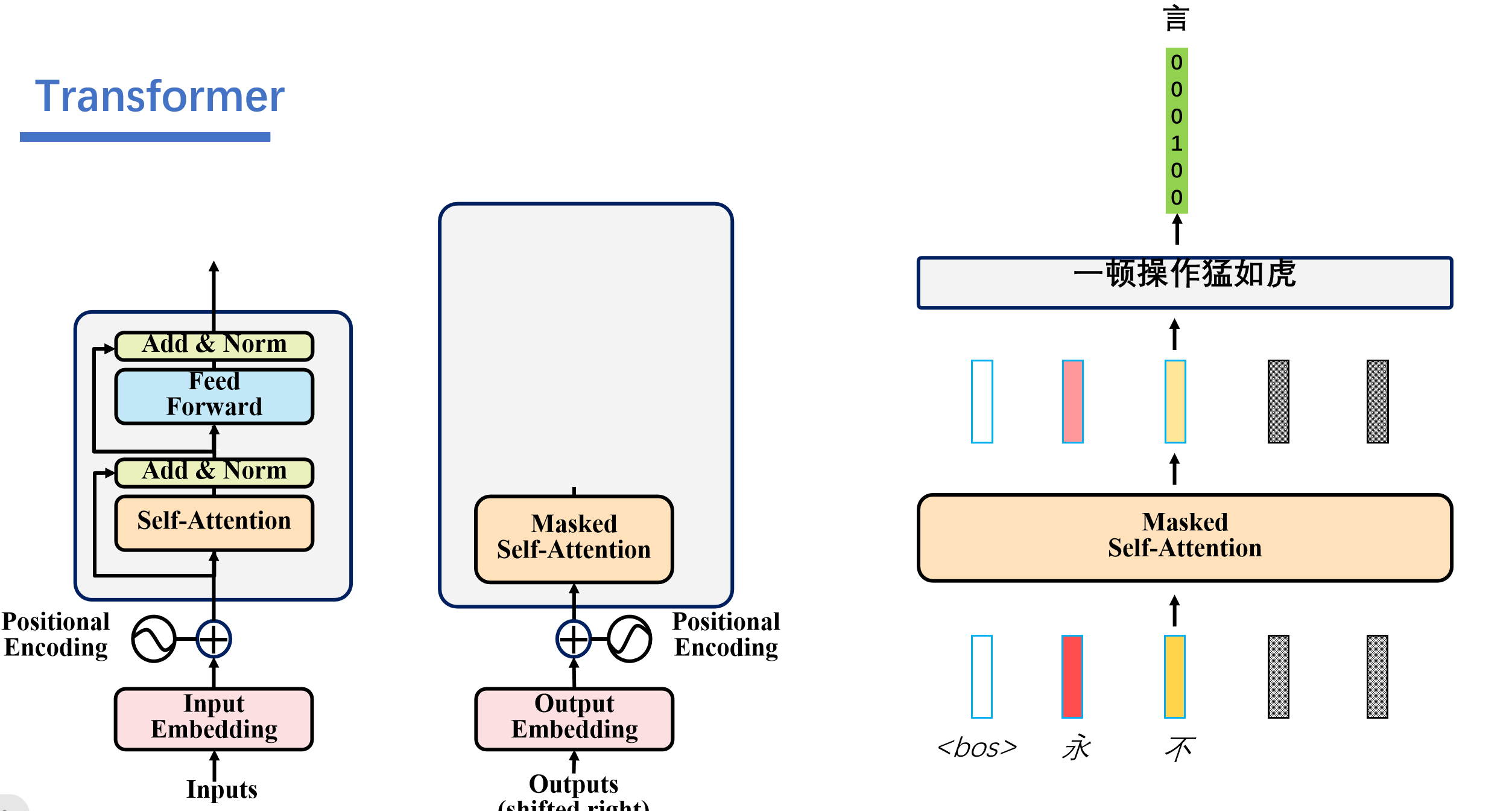
最后由<bos>,永,不,言,弃预测出来<eos>，就结束了。
然后这里就会用到Masked-Attention。我们再预测前面的时候需要将后面的给遮起来。
具体操作是这样的：我们将后面的权重设为负无穷。



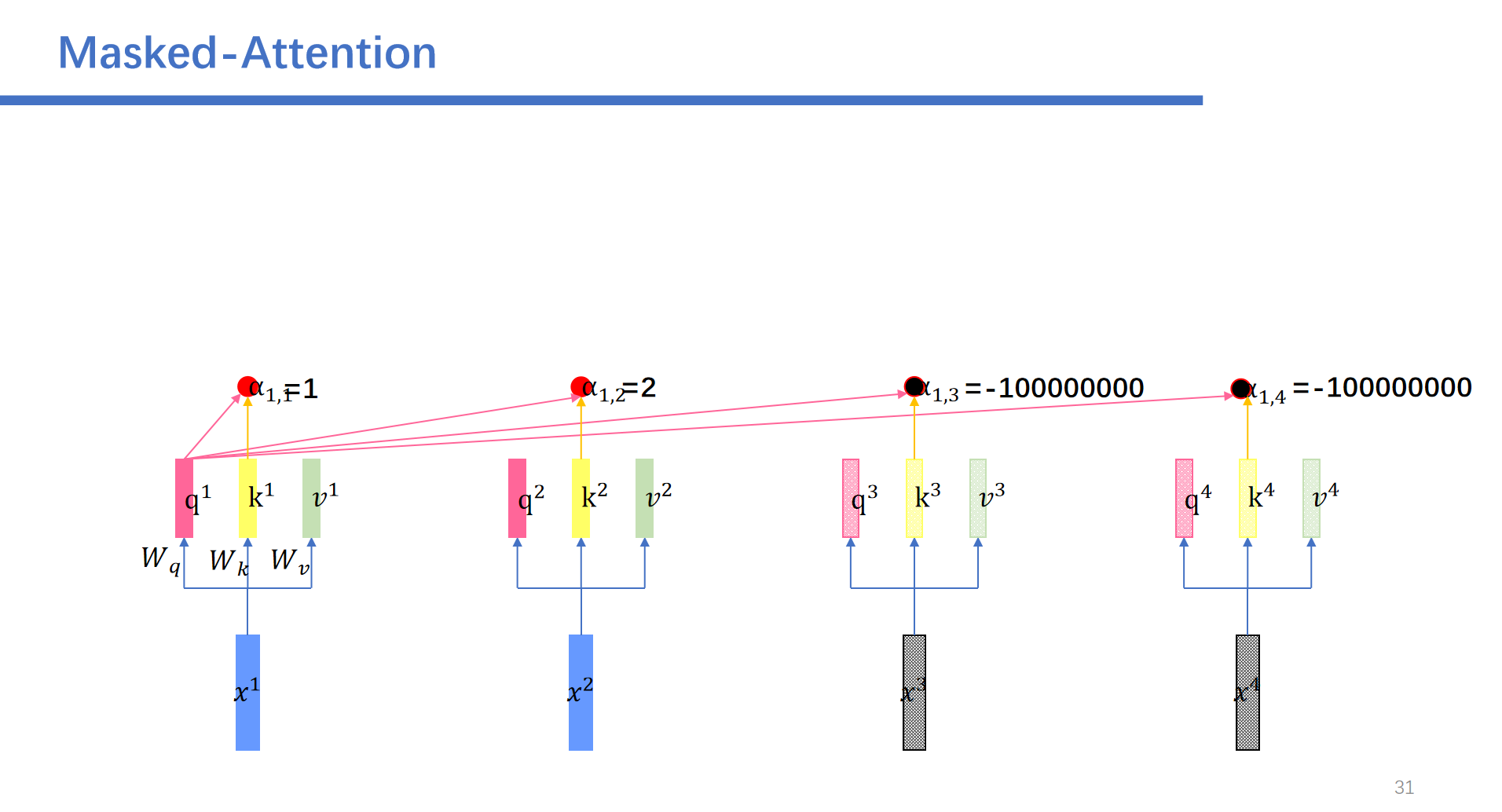
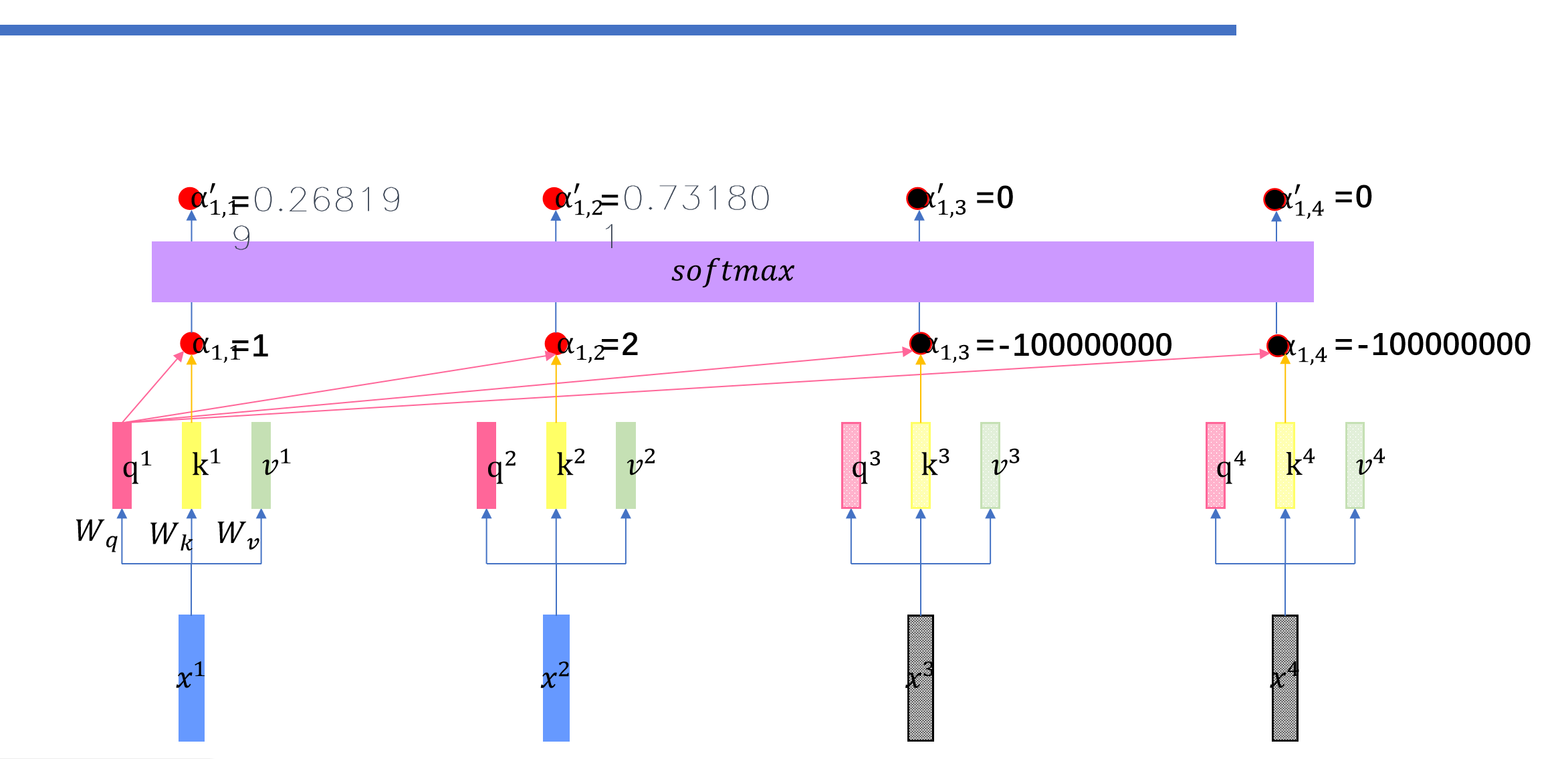
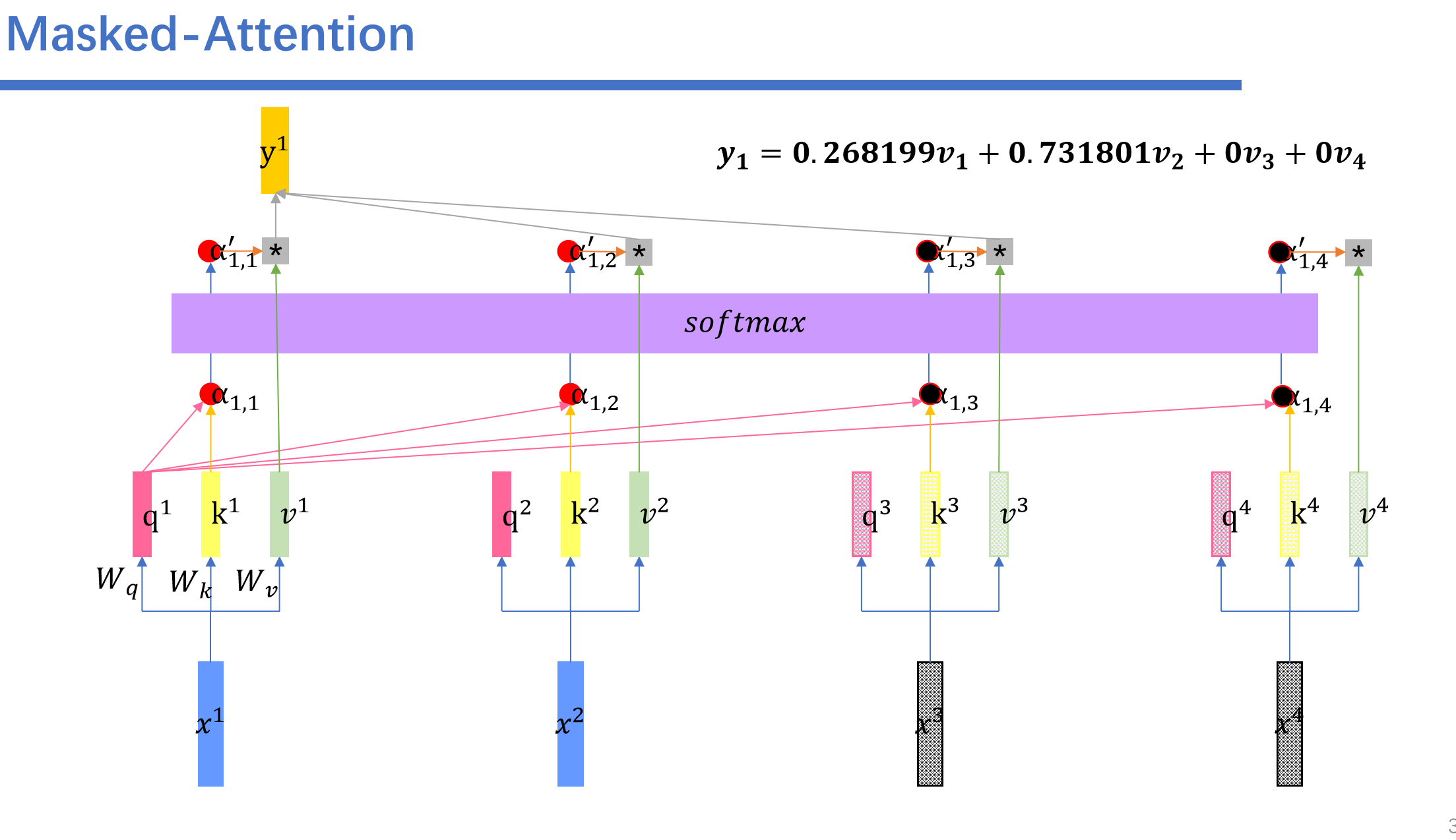
比如说我们，再预测到了永，不之后，之后的向量都是随机的数，然后我们进行masked self-attention之后，随机的数字对应的矩阵都是0.

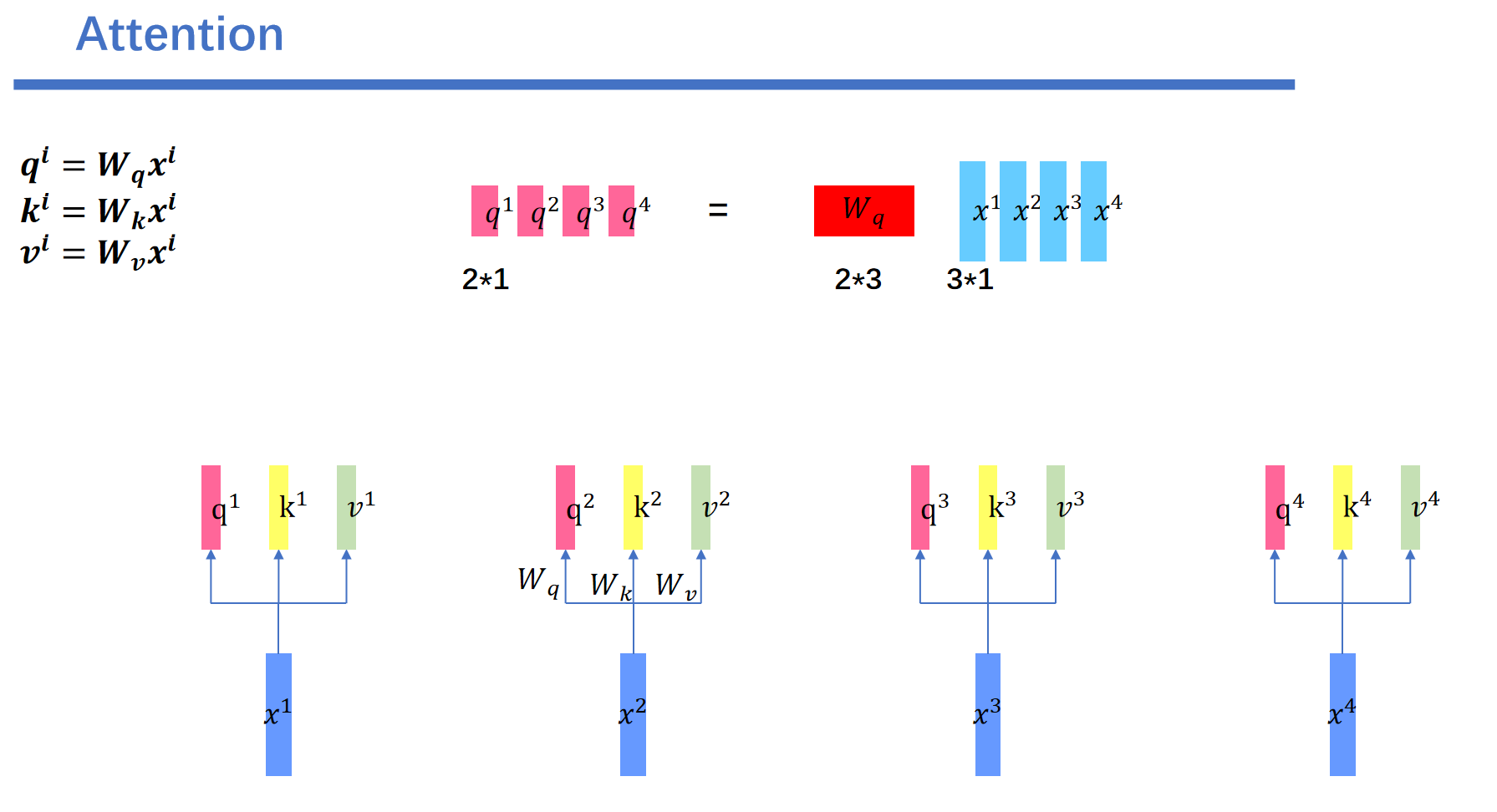
3.self attention中维度分析

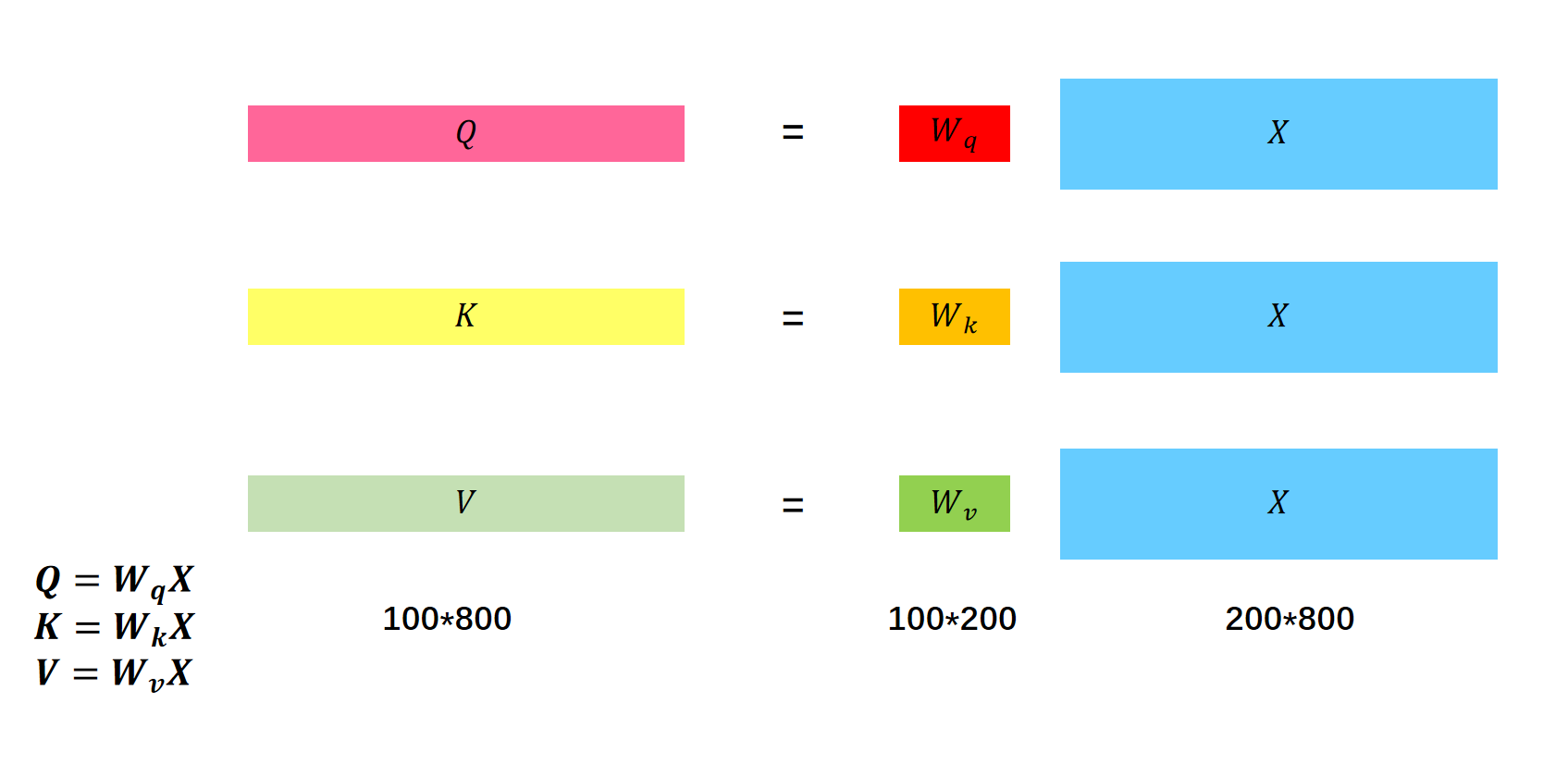
首先是\(x\)向量分别乘上\(W^q,W^k,W^v\)，生成\(q,k,v\)向量。这里我们以生成\(q^2\)向量为例子。目标\(q^2\)的维度是2，输入向量x的维度是3。那么我们就需要训练一个\(2 \times 3\)的矩阵进行转换。

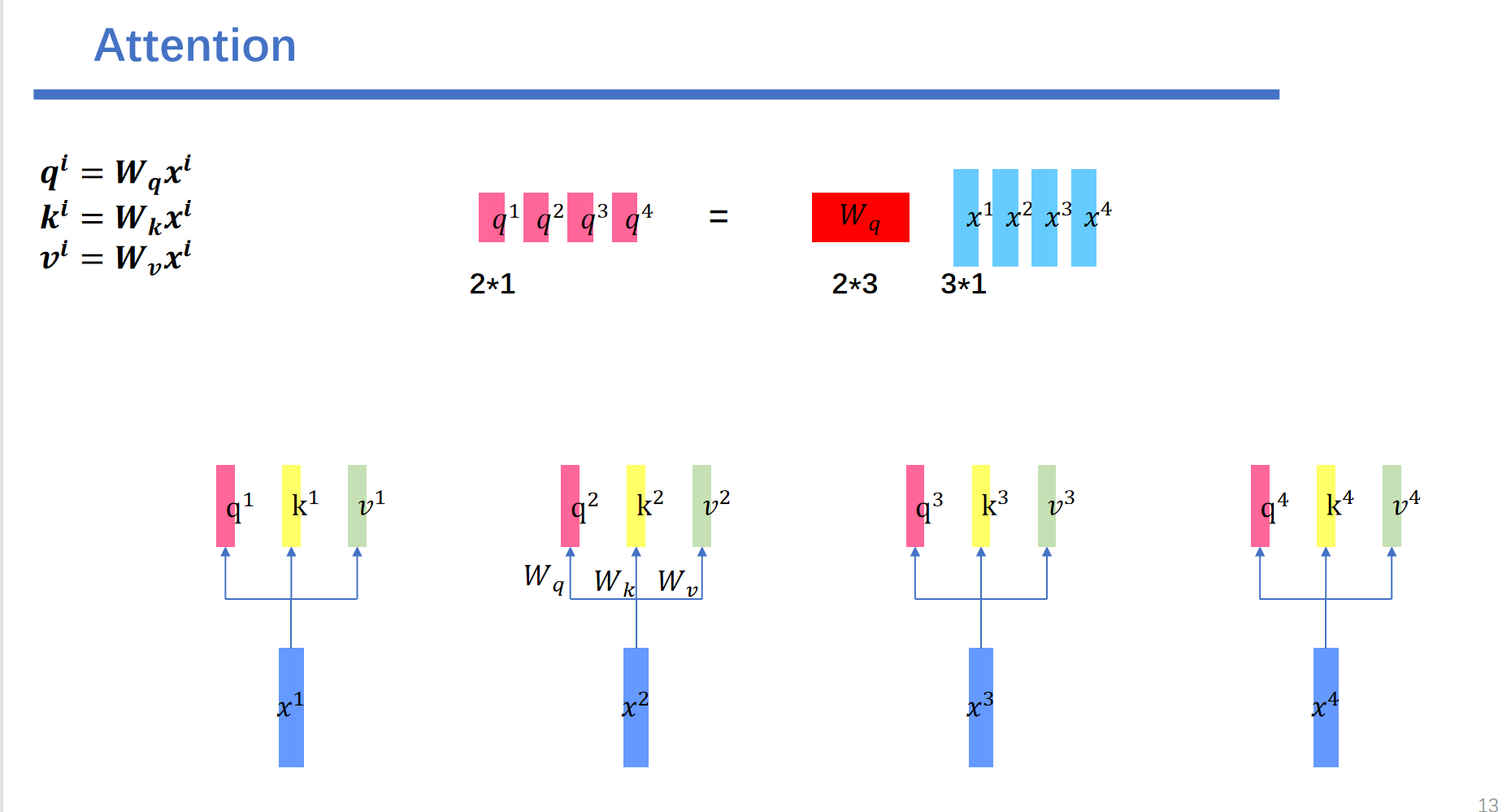
同样的\(x^3\)乘上\(W^q\)会得到\(q^3\)。\(x^4\)乘上\(W^q\)会得到\(q^4\)，\(x^1\)乘上\(W^q\)会得到\(q^1\)。

例如这个例子：

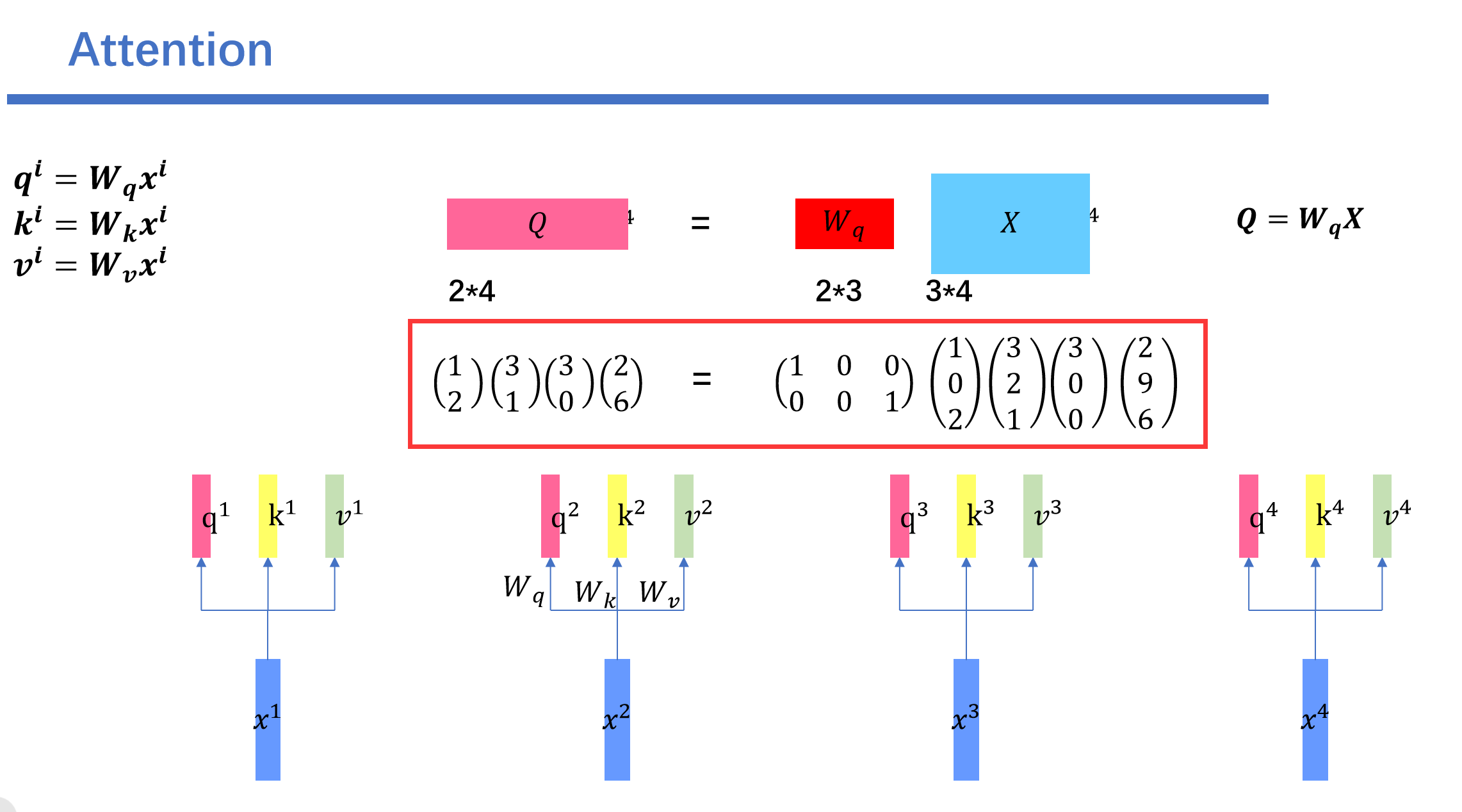
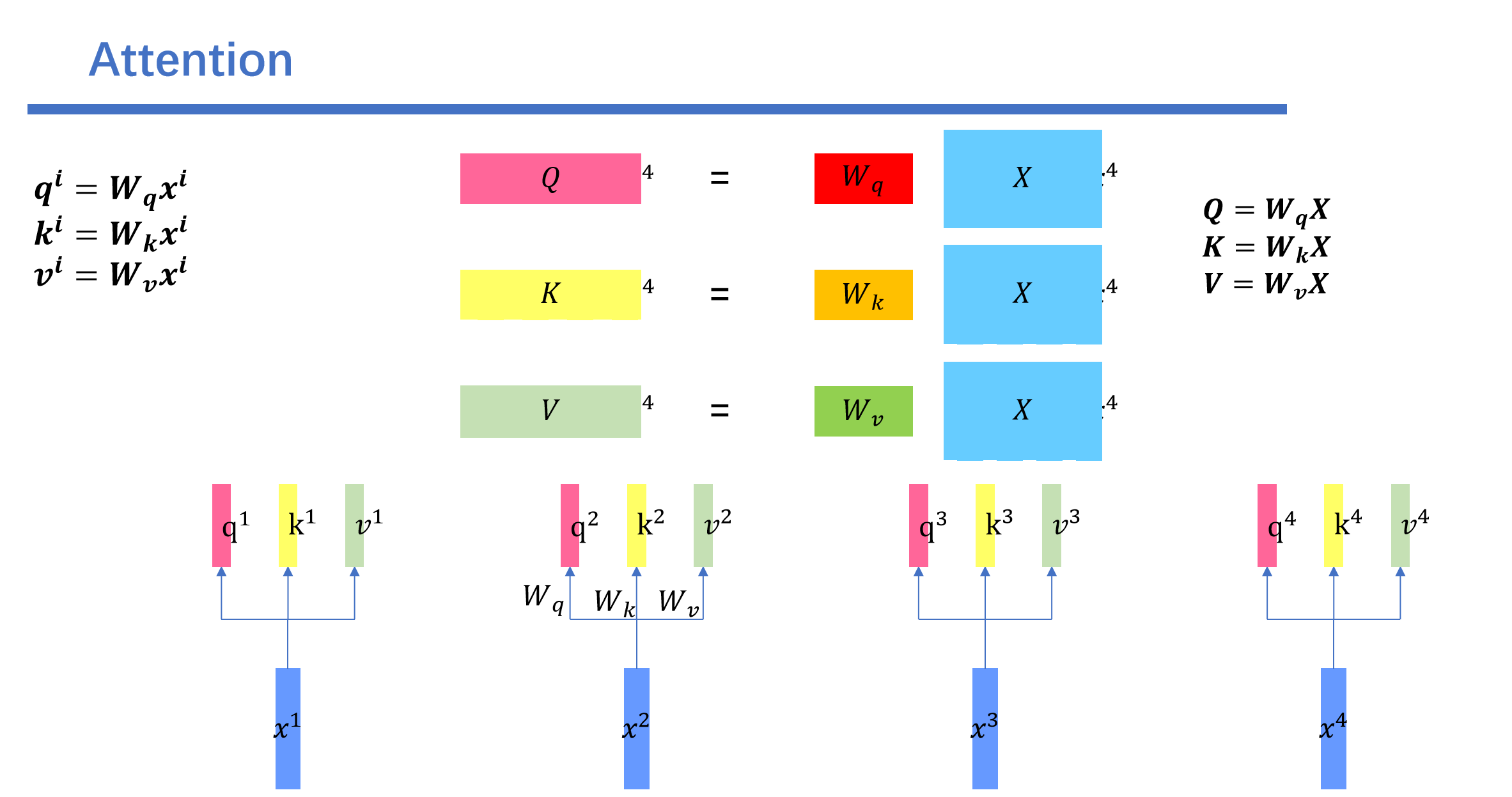
和前面一样我们算出来\(Q,K,V\)

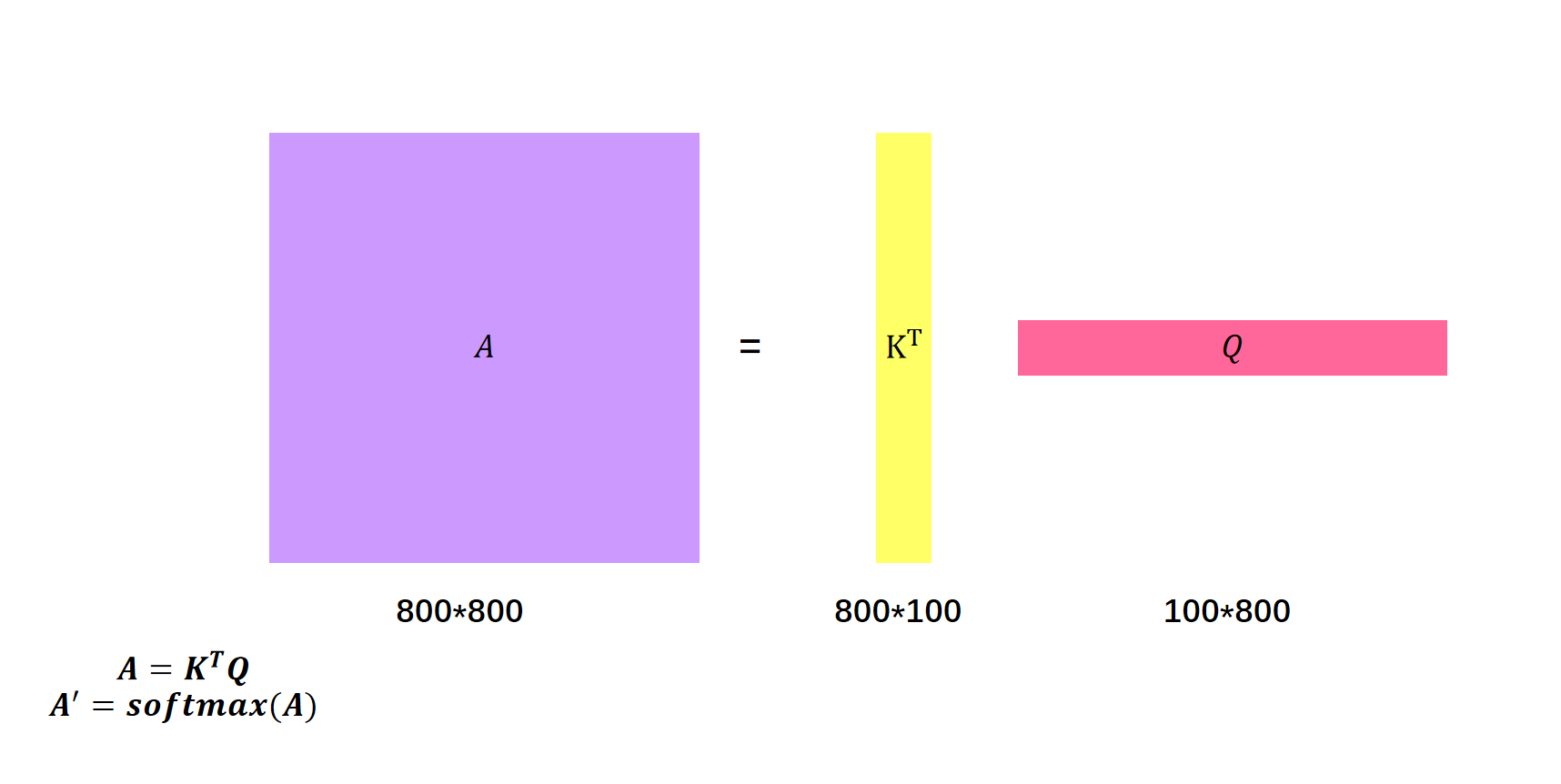
接下来每一个\(q\)都会和每一个\(v\)做内积计算计算attention score.
这里我们以\(q^2\)为例子：\(q^2\)与\(k^1\)内积得到\(a_{2,1}\)。

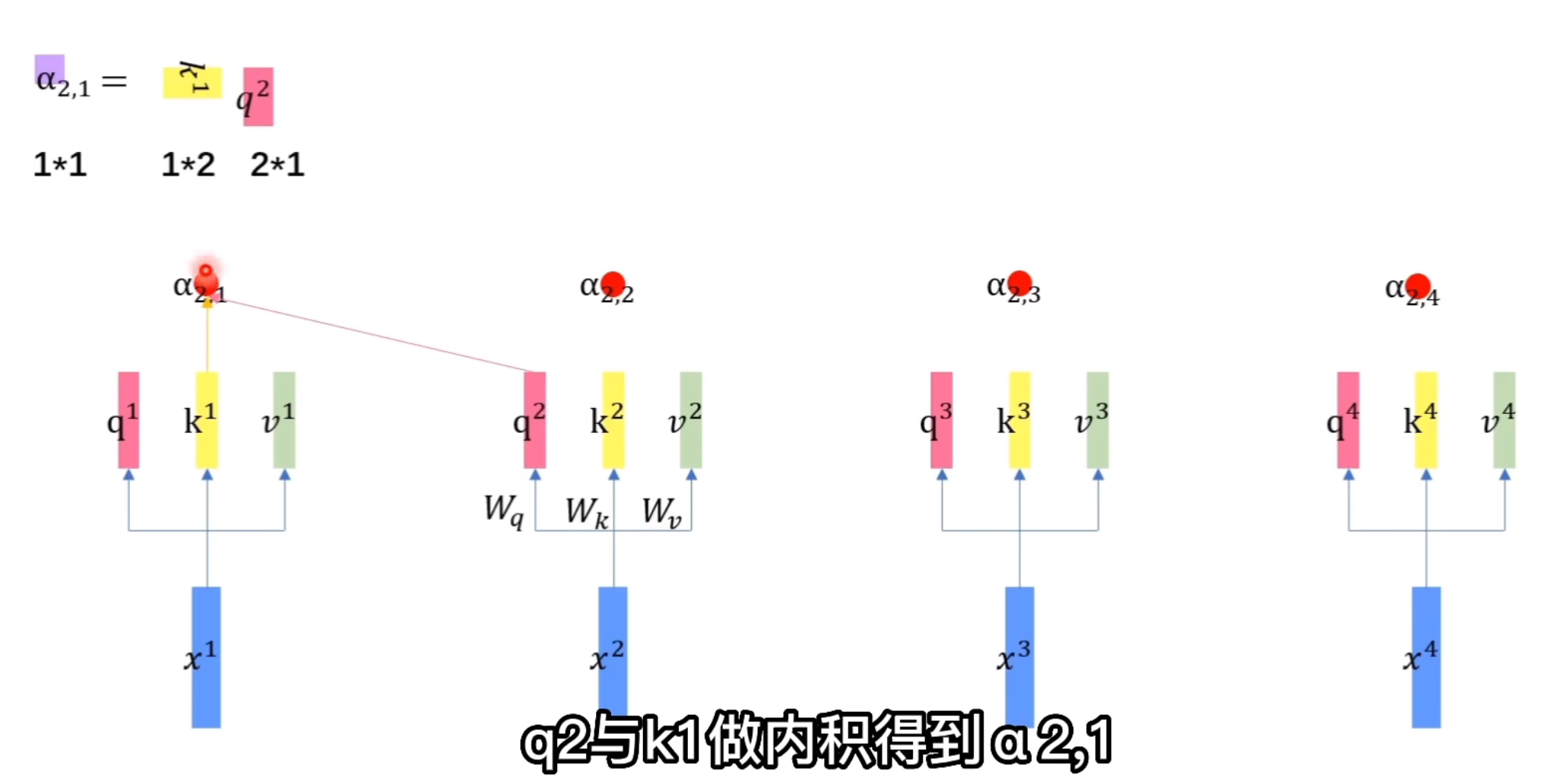
\(q^2\)与\(k^2\)内积得到\(a_{2,2}\)。\(q^2\)与\(k^3\)内积得到\(a_{2,3}\)。
\(q^2\)与\(k^4\)内积得到\(a_{2,4}\).我们将\(k^1\)进行转置,然后用\(q^2\)左乘转置后的\(k^1\)，就得到了\(a_{2,1}\)。这里要做四次矩阵运算。为了提高并行性，我们将其整合成一次。

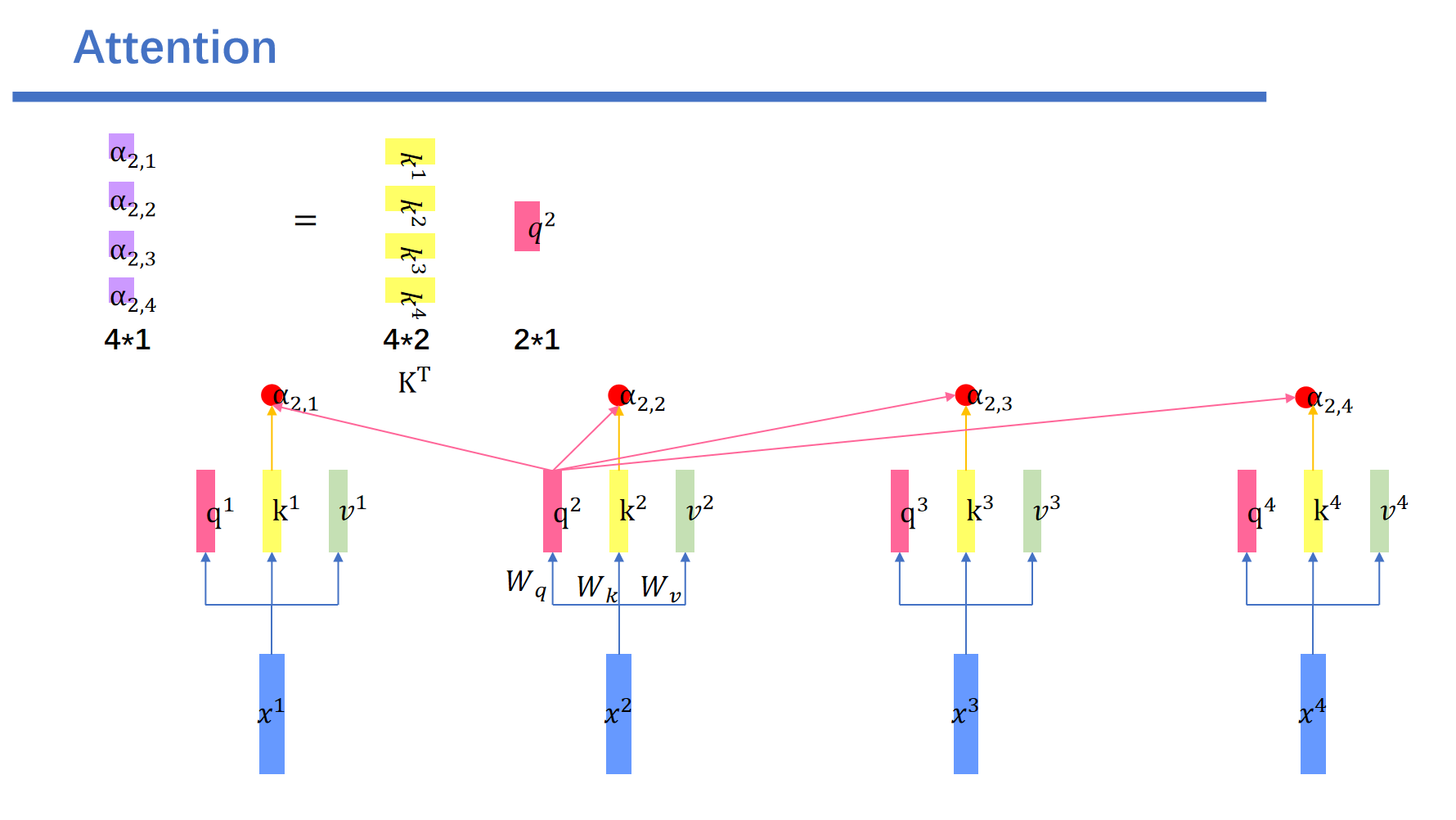
然后这个矩阵就是通过\(q^2\)查询的每个元素的attention score。
同样的我们用\(q^3\)乘以矩阵\(k^T\)就得到了\(q^3\)的全部attention score。

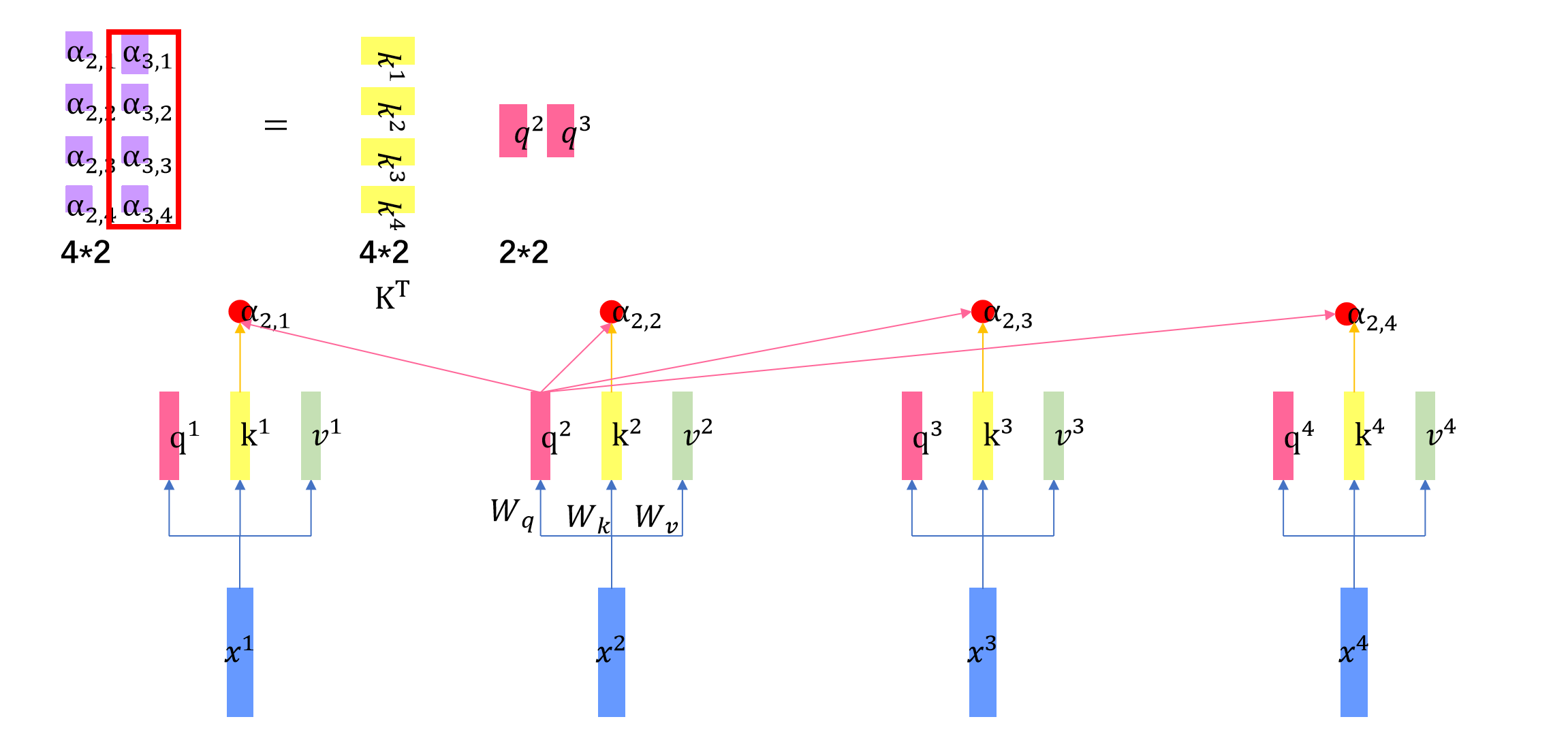
然后我们用全部的：

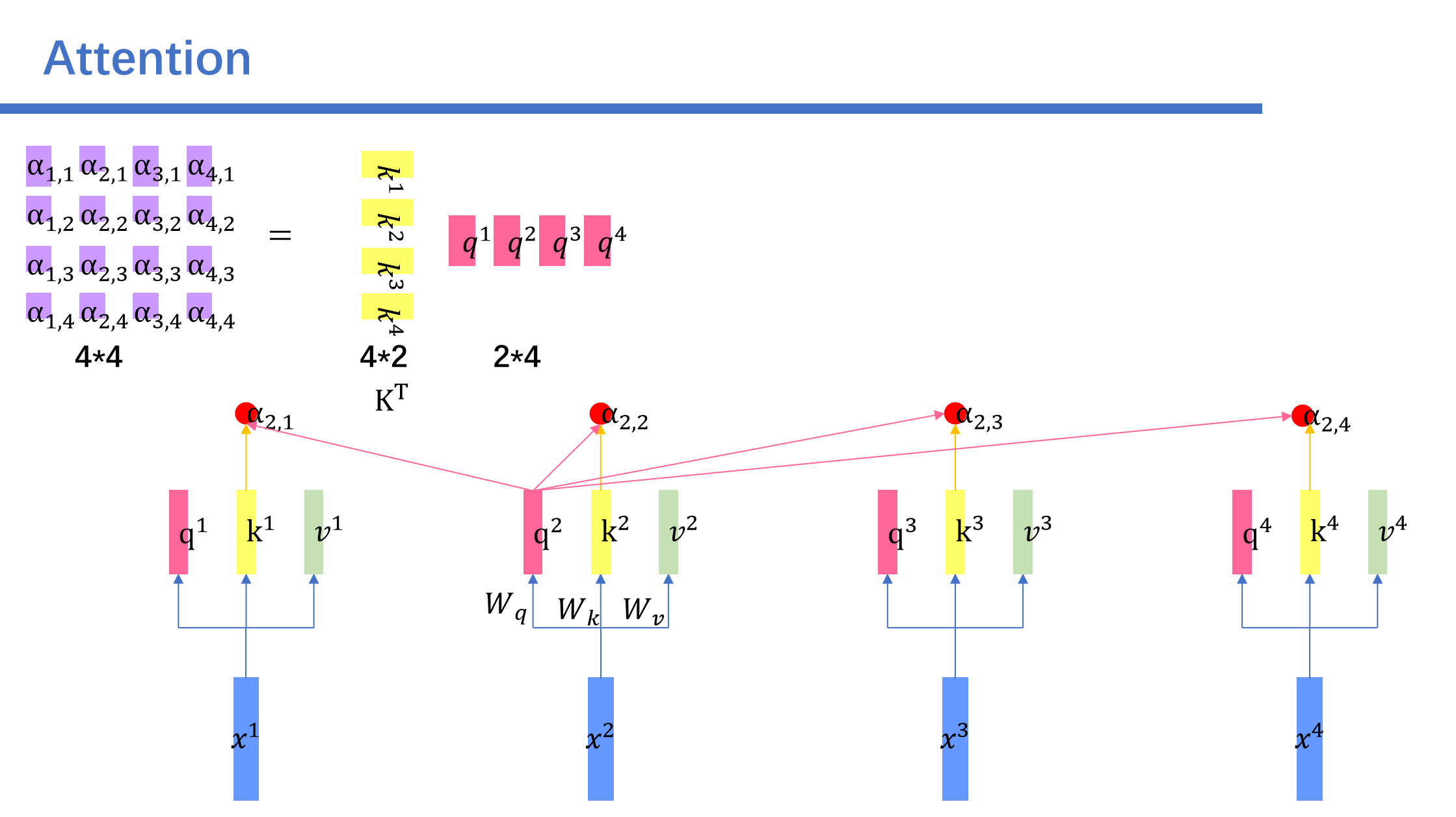
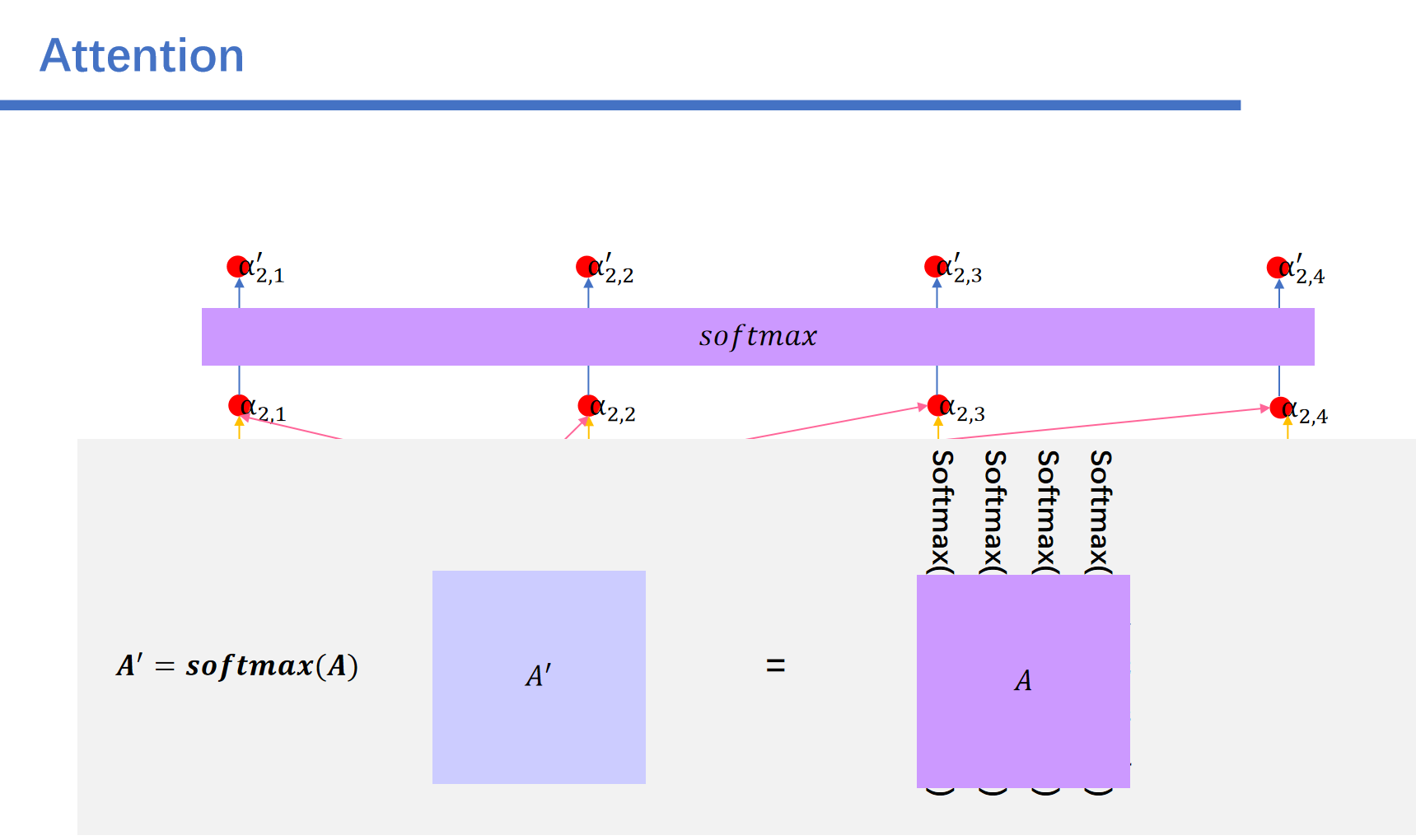
我们将\(a\)矩阵记为A。

之后对每一列的元素进行softmax之后：得到\(a'\)向量。


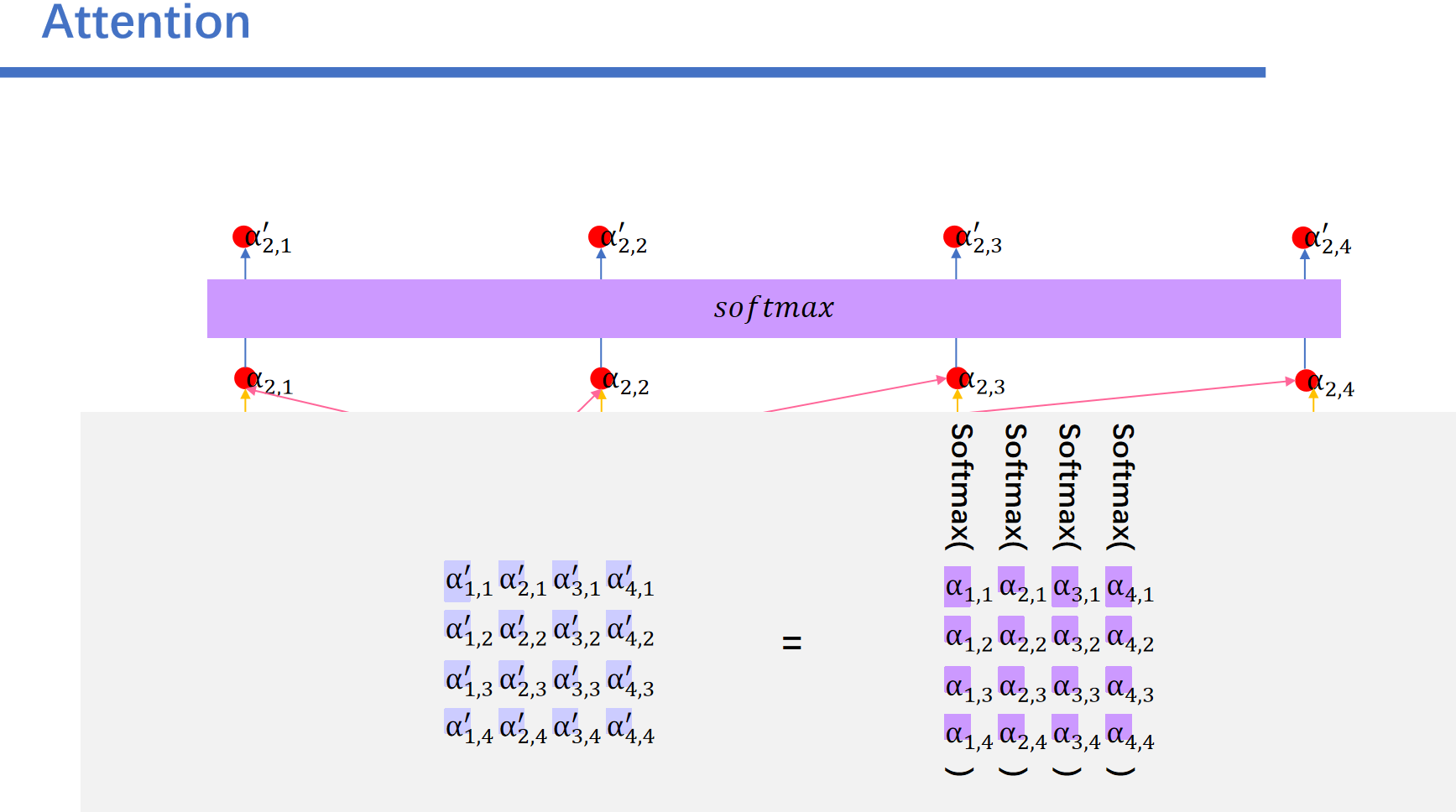
最后我们将刚刚得到的\(a'\)作为权值，和所有的\(v\)向量相乘相加。即可得到我们最终的输出\(y\)。

例如我们\(y^2\)的结果就是这样的：最后一行是换成矩阵乘法的方式。

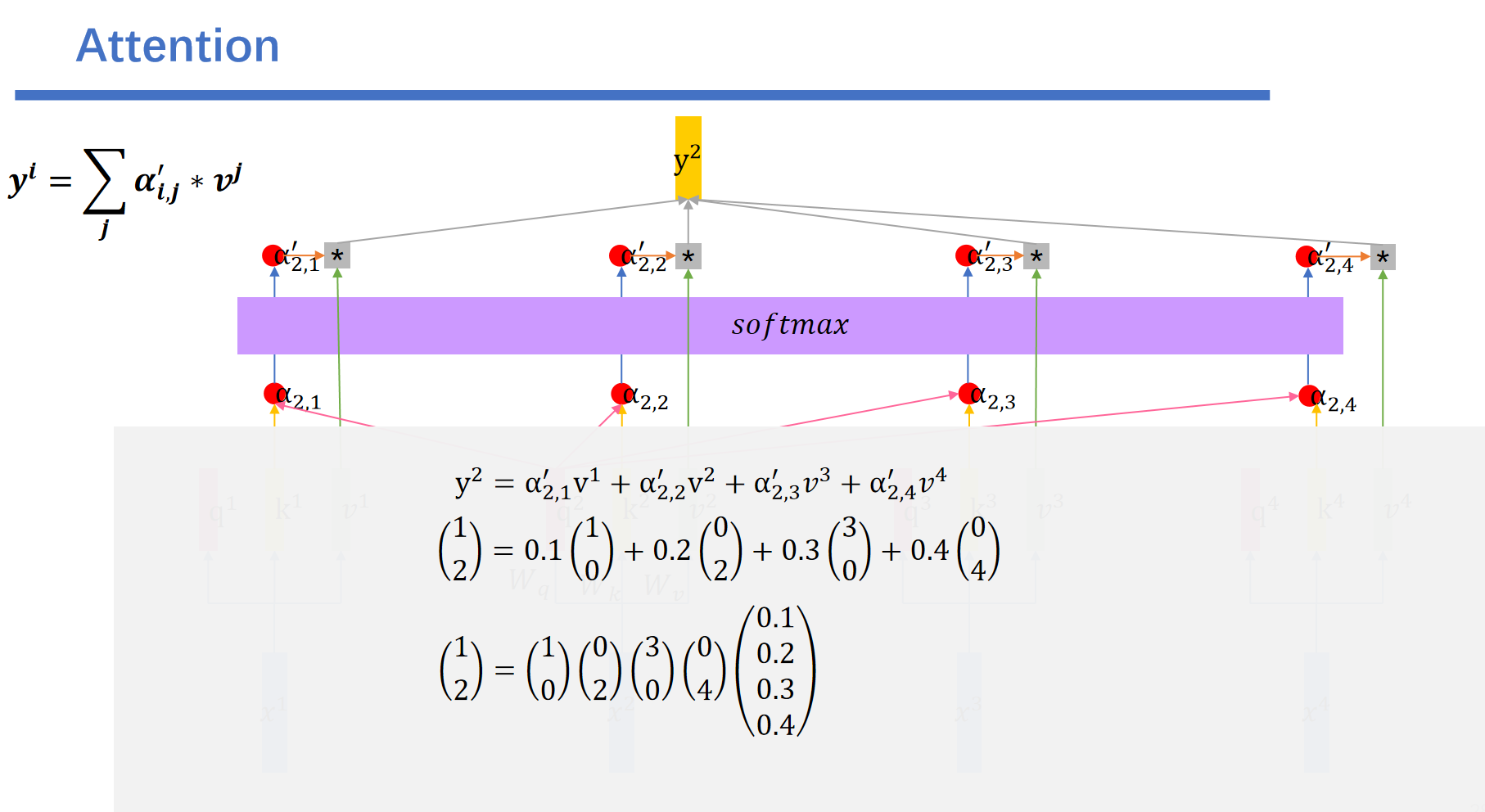
我们将其符号化就是这样的：

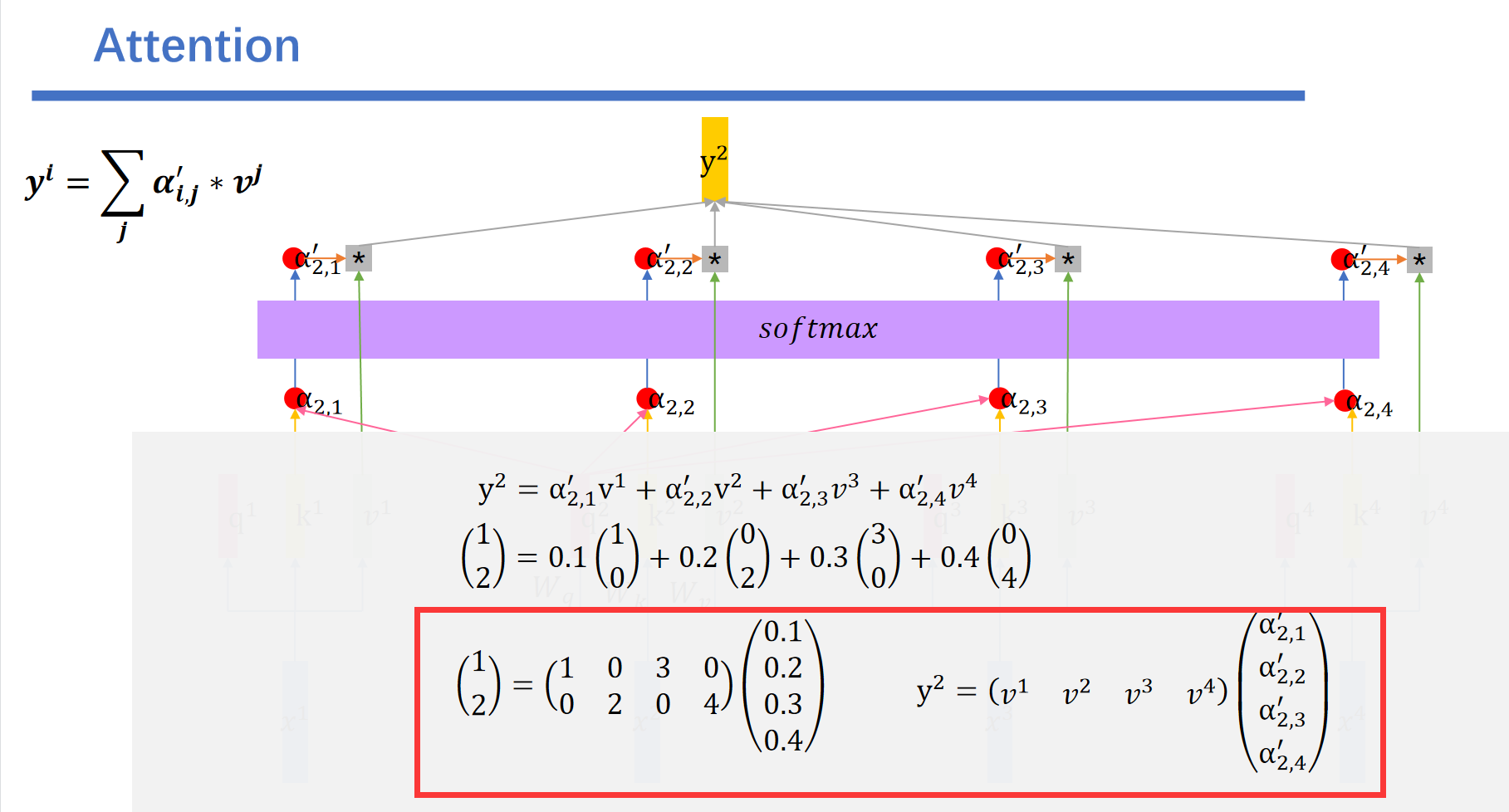
同样的我们可以用这种方法得到\(y^3\),\(y^4\),\(y^1\):


我们把左右拼接好的y向量叫做矩阵Y,左右拼接好的v向量叫做矩阵V。

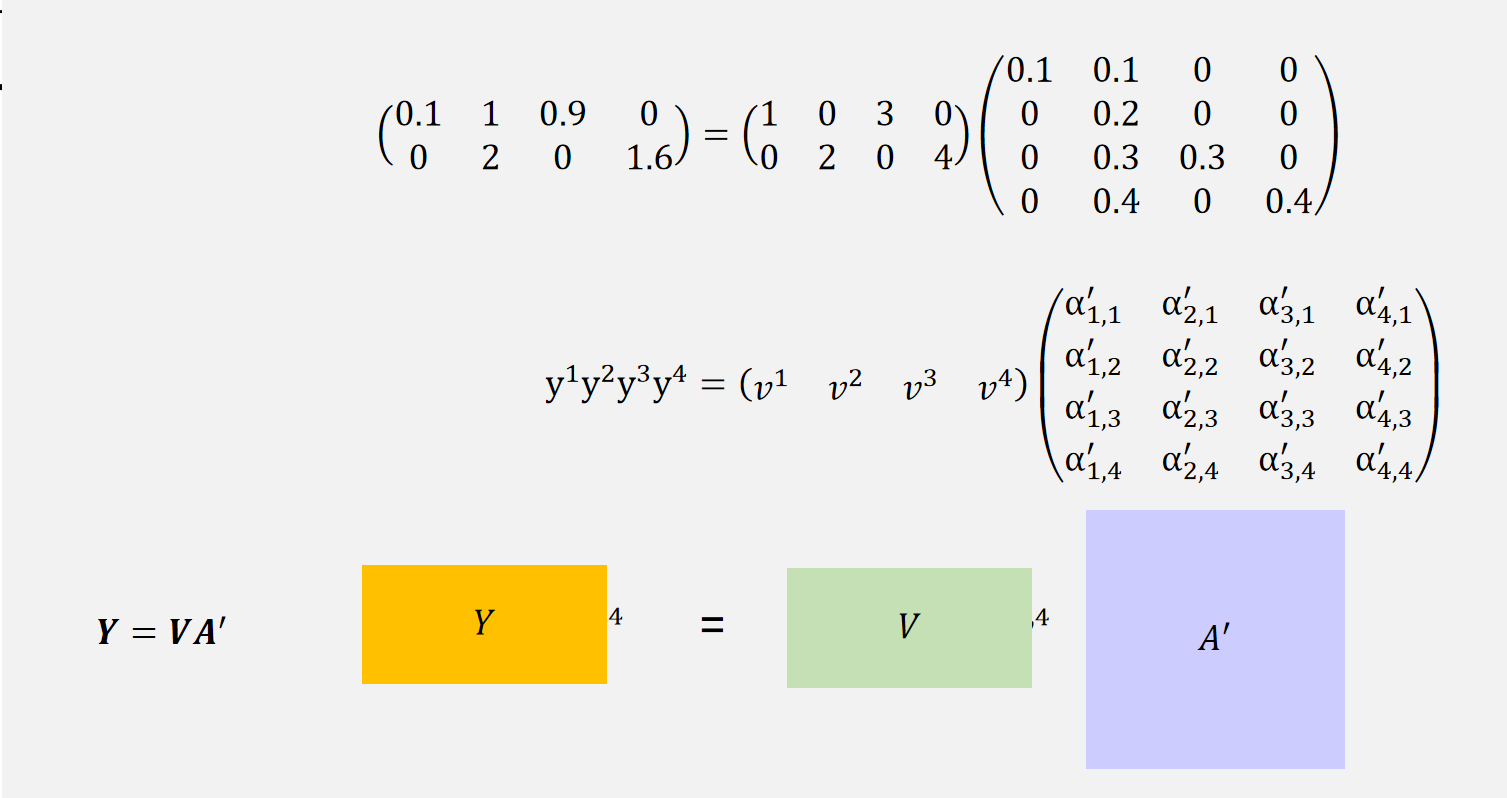
这就是attention的全部运算。

我们用一个例子总的回顾一下：
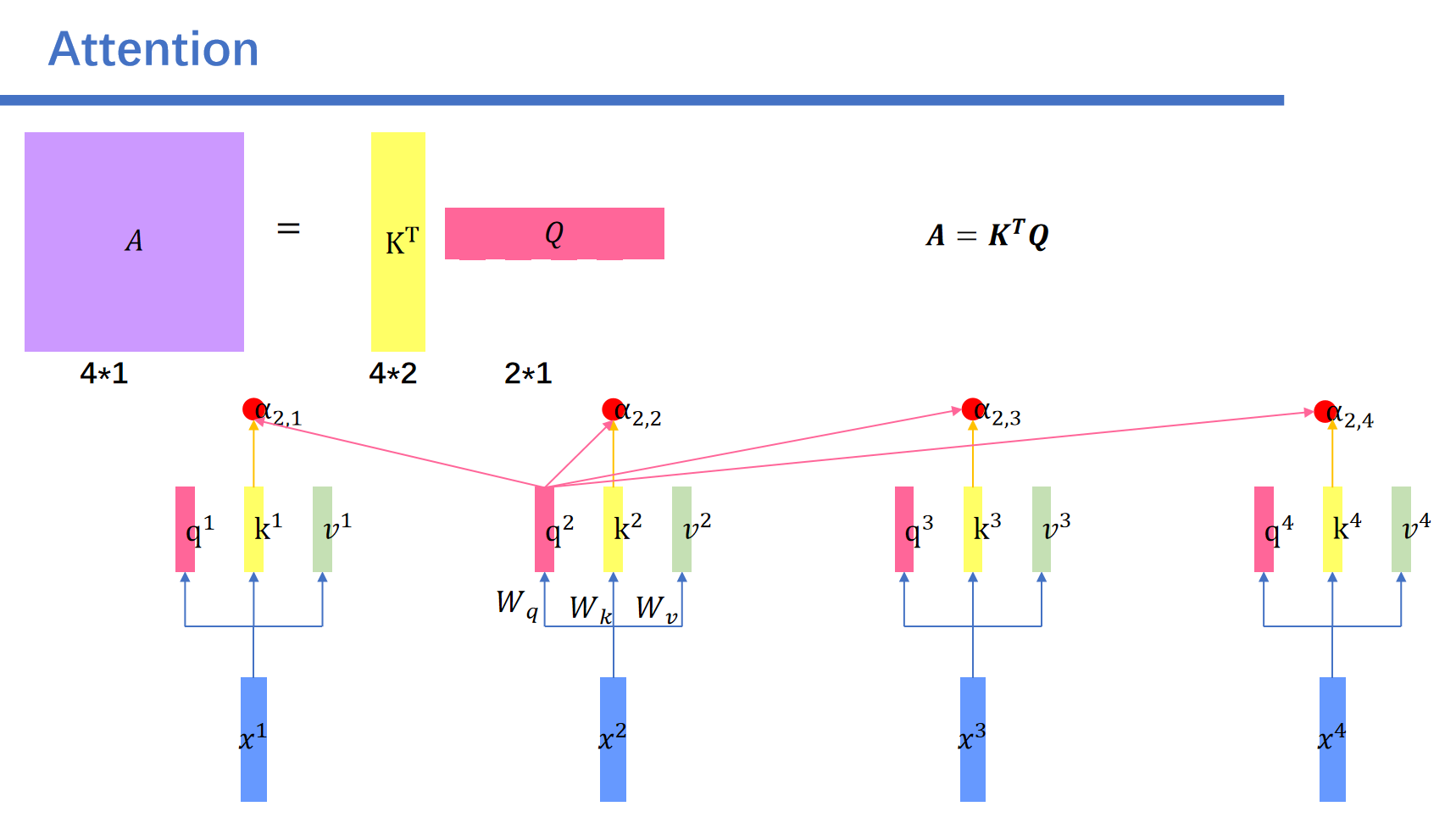
先通过\(x\)矩阵生成\(Q,K,V\)。

然后用\(K^T\)乘上\(Q\)得到attention score:\(A\)。

之后对\(A\)进行softmax得到\(A'\)

之后用\(A'\)乘上矩阵\(V\)就得到了输出\(Y\)。

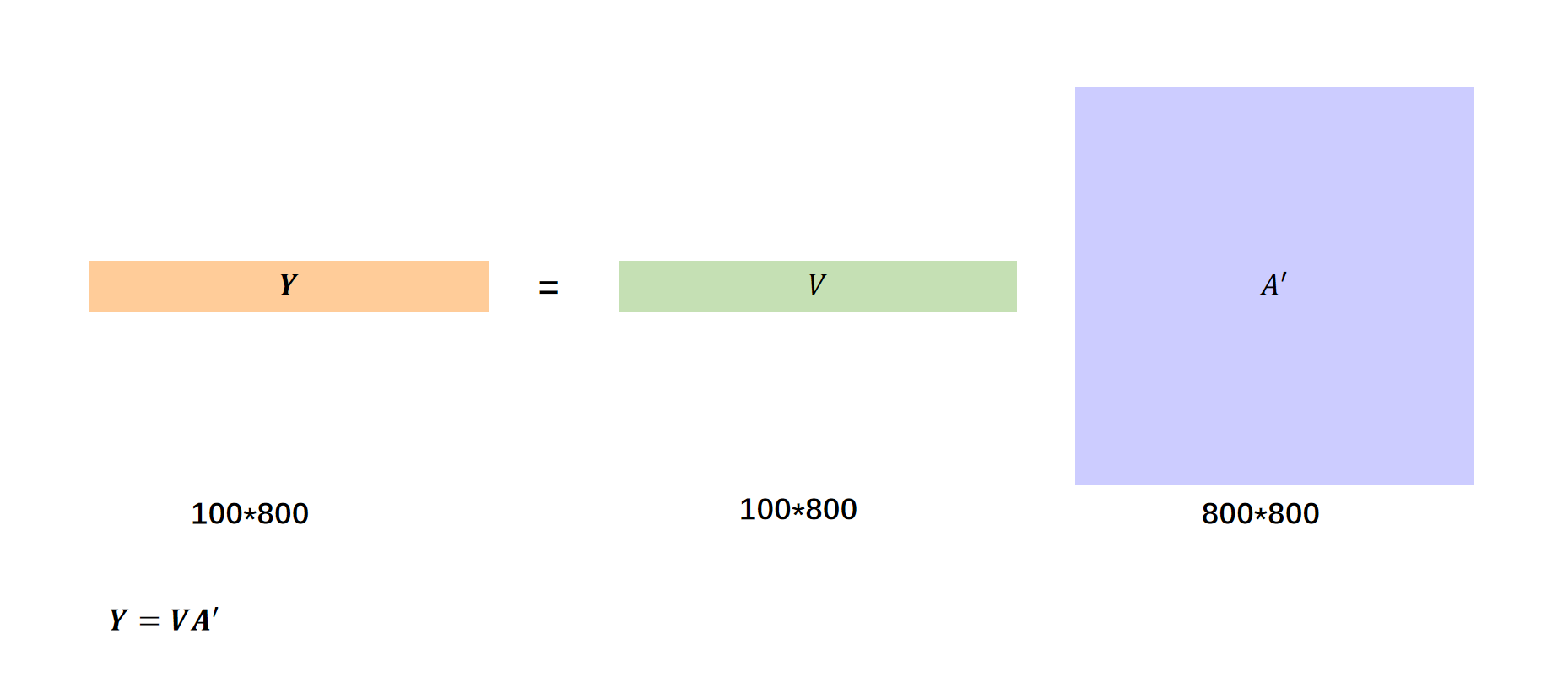
4 Multi-head Attention

以及两个词之间的相关关系，可能并不止一种，因此，我们使用多个头（head）来对不同的相关性进行分析计算。

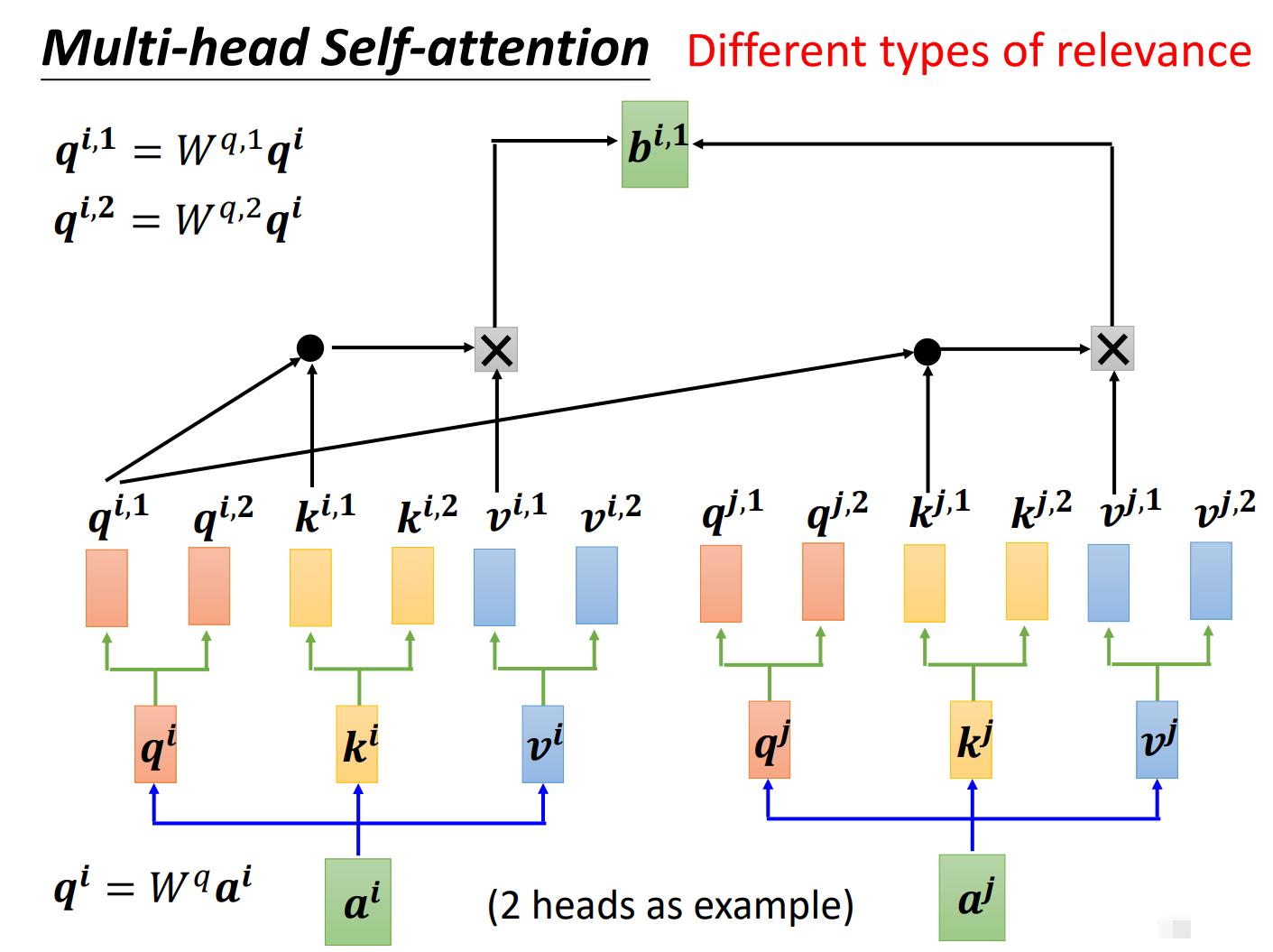
如下图所示，假如我们现在有两个头，那么我们需要对每个头分别进行学习，得到每个头中的\(W{^q}{^i}, W{^k}{^i}, W{^v}{^i}\)，然后再进行自注意力的计算。

在第一个头中，我们得到\(b{^i}{^,}{^1}\), 如下图所示：

在第二个头中，我们得到\(b{^i}{^,}{^2}\), 如下图所示：

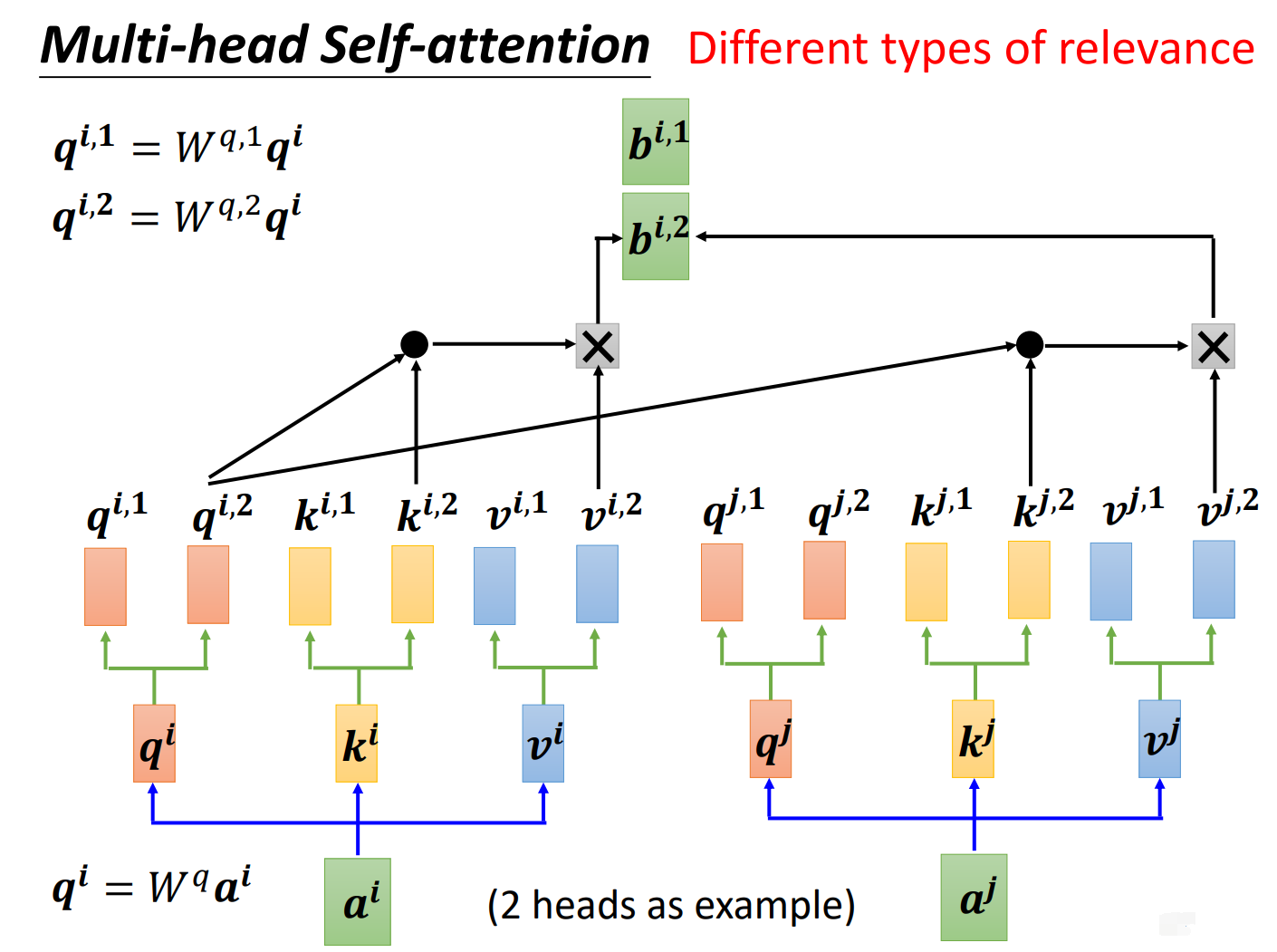
\(b{^i}{^,}{^1}和b{^i}{^,}{^2}\)关注的是不同类型的相关性。

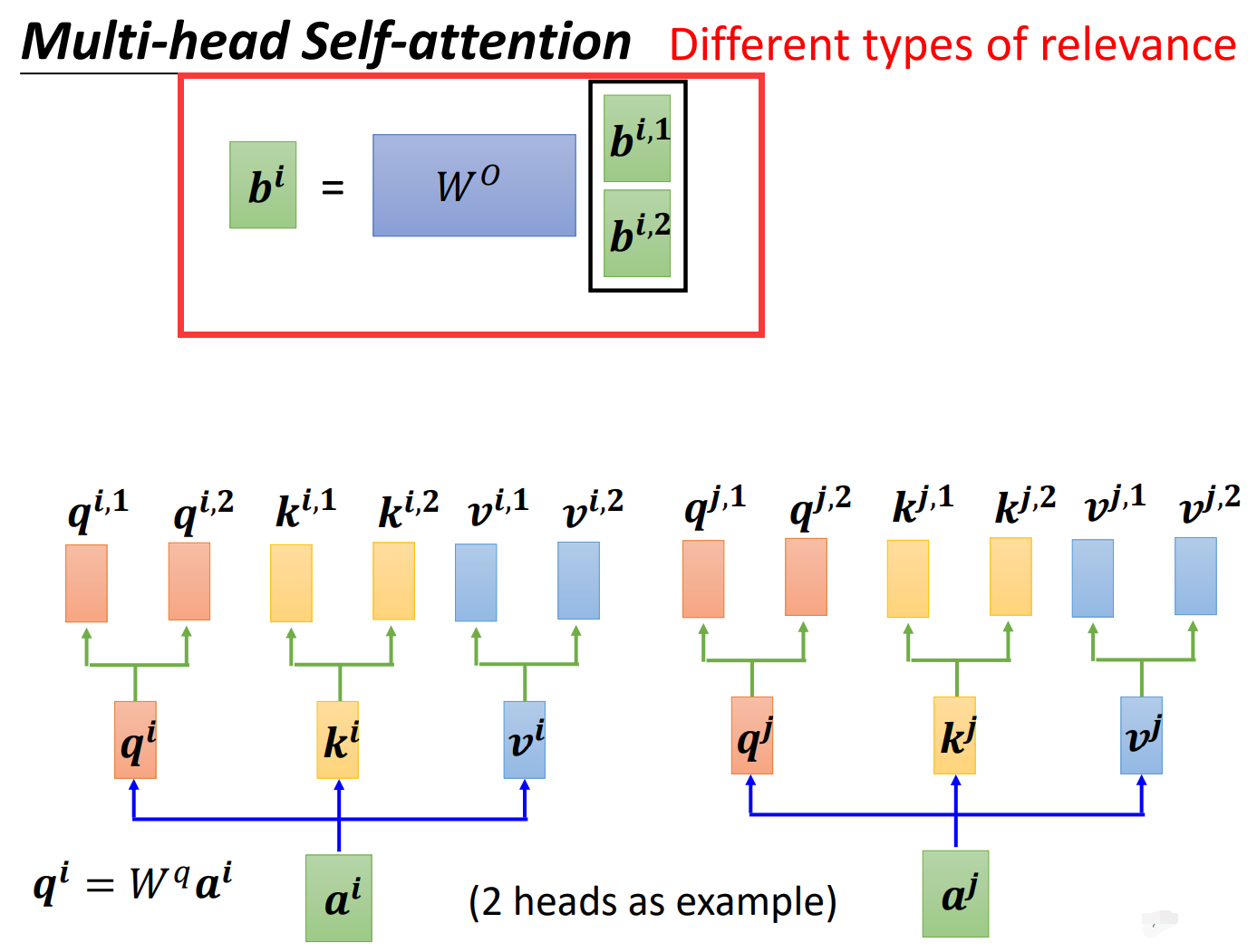
得到了\(b{^i}{^,}{^1}和b{^i}{^,}{^2}\)之后，我们还是合并\(b{^i}{^,}{^1}\)和\(b{^i}{^,}{^2}\)得到一个合并矩阵，然后与\(W{^o}\)相乘，这样可以保证Multi-head Attention中输入矩阵和输出矩阵的维度相等，同时这也是和self attention不同的地方，多了一个\(W^o\)。得到汇总了两个不同相关性信息的\(b{^i}\)。如下图所示：

我们从矩阵维度的角度来看看Self attention和Multi-head Attention：
上图提示了一个输入为两个单词\([Thinking, Matchines]\)的序列在经过自注意力构建后的变换过程：

Self attention

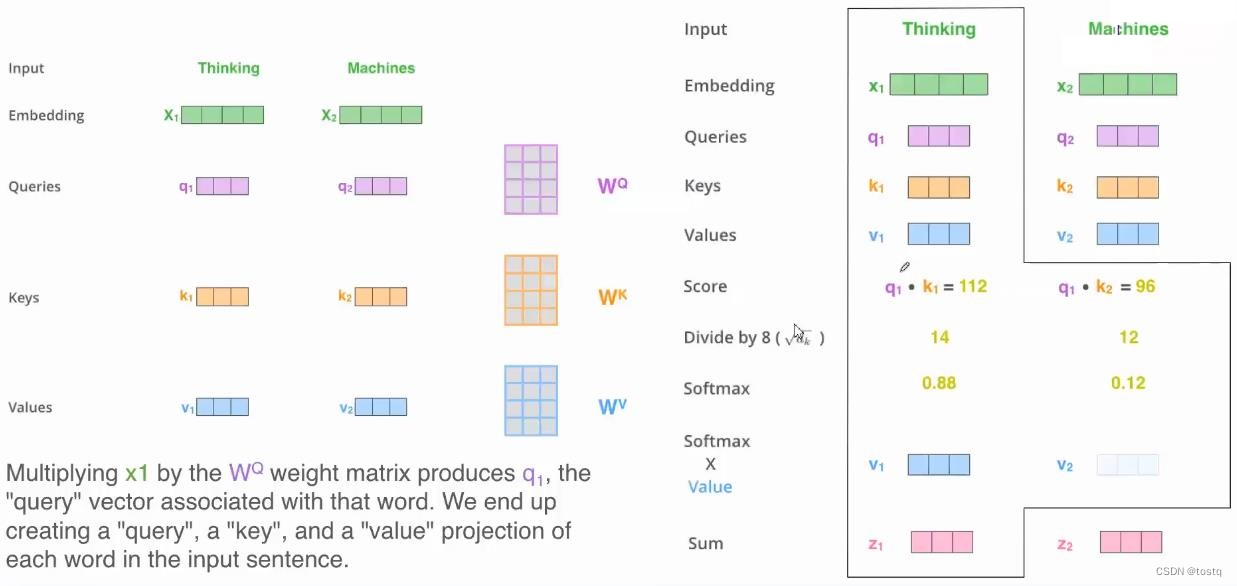
• 通过Embeding层，两个单词的one-hot向量转换为embedding向量\(X=[x_1, x_2]\)

• 通过三组矩阵运算得到query、key、value值，这三组矩阵的输入都是原来同一个输入向量\([x_1,x_2]\)，这也是被称之为自注意力的原因。
  \(\\ Q=\begin{bmatrix} q_1\\ q_2 \end{bmatrix}_{2\times d_q}=\begin{bmatrix} x_1\\ x_2 \end{bmatrix}_{2\times d_x} *W^Q_{d_x \times d_q}\\ K=\begin{bmatrix} k_1\\ k_2 \end{bmatrix}_{2\times d_k}=\begin{bmatrix} x_1\\ x_2 \end{bmatrix}_{2\times d_x} *W^K_{d_x \times d_k}\\ V=\begin{bmatrix} v_1\\ v_2 \end{bmatrix}_{2\times d_v}=\begin{bmatrix} x_1\\ x_2 \end{bmatrix}_{2\times d_x} *W^K_{d_x \times d_v}\)

• 计算query、key间的相似度得分，为了提升计算效率，此处采用缩放点积注意力，其需要query、key向量的维度是相等的，并且都满足零均值和单位方差，此时得分表示：
  \(\\ score(q, k)=\frac{q\cdot k }{\sqrt{d_k}}\\ Score(Q, K)_{2\times 2}=\begin{bmatrix} s_{11} & s_{12}\\ s_{21} & s_{22}\end{bmatrix}_{2 \times 2}=\frac{1}{\sqrt{d_k}}\begin{bmatrix} q1 && q1\\ q2 && q2 \end{bmatrix}_{2\times d_q}\begin{bmatrix} k1 & k2 \\ k1 & k2 \end{bmatrix}_{d_q \times 2}\)

• 对相似度得分矩阵求softmax进行归一化（按axis=1维进行），在实际中由于进行transformer中的输入序列要求是定长的，因此会有补余向量，此时这里softmax会有一个掩蔽操作，将补余部分都置为0。
  \(softmax(\begin{bmatrix} \xrightarrow[]{s_{11} \ s_{12}}\\ \xrightarrow[]{s_{21} \ s_{22}}\end{bmatrix})=\begin{bmatrix} p_{11} & p_{12}\\ p_{21} & p_{22} \end{bmatrix}\)

• 乘以value向量得到输出z：
  \(Z=\begin{bmatrix} z_1 \\ z_2 \end{bmatrix}= \begin{bmatrix} p_{11} & p_{12}\\ p_{21} & p_{22} \end{bmatrix}\begin{bmatrix} v_1 \\ v_2 \end{bmatrix}\)

Multi-head Attention

多头注意力是多组自注意力构件的组合，上文已经提到自注意力机制能帮助建立包括上下文信息的词特征表达，多头注意力能帮忙学习到多种不同类型的上下文影响情况，比如"今天阳光不错，适合出去跑步"，在不同情景下，"今天"同"阳光"、"跑步"的相关性是不同，特别是头越多，越有利于捕获更大更多范围的相关性特征，增加模型的表达能力。

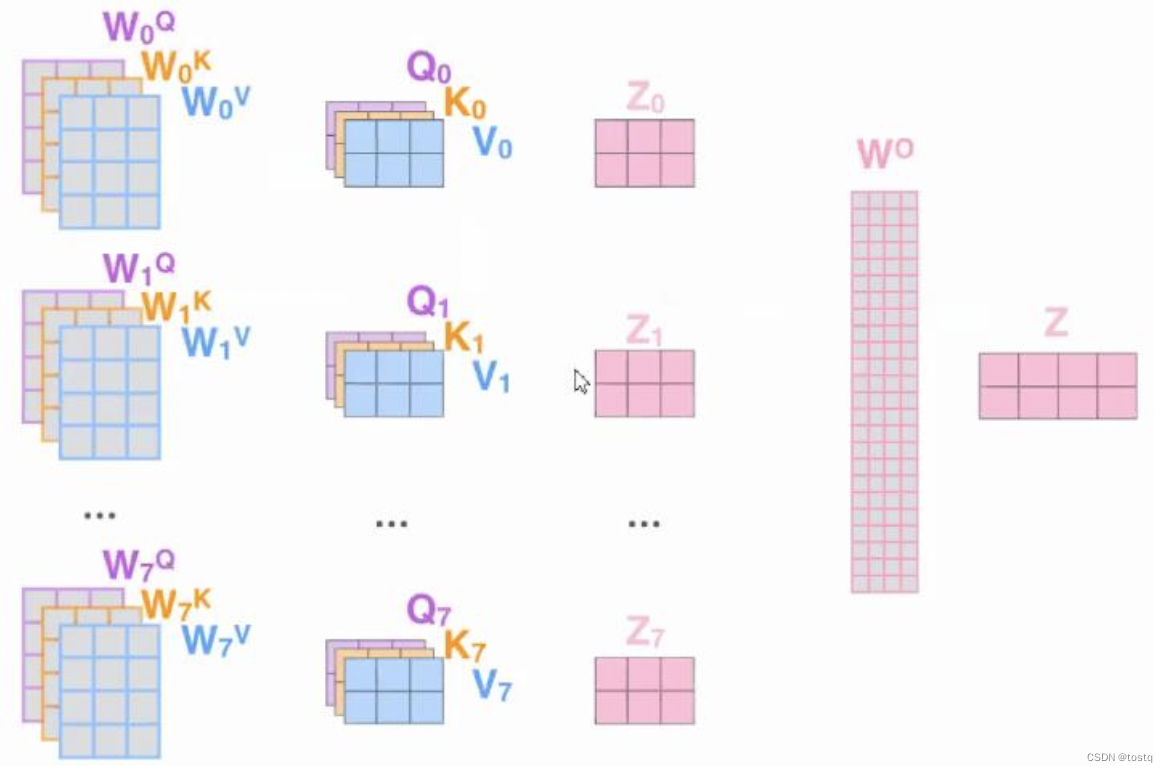
上图描述了多头注意力的处理过程，其实际上将多个自注意机制的产出再经过参数矩阵得到一个新输出。我们将上述自注意步骤引入多头情况，介绍如何通过矩阵来计算，其由3组自注意力组合，输入为2个单词的序列。

• query、key、value表征向量的计算
  \(\\ \begin{bmatrix} q^1_1 & q^2_1 & q^3_1\\ q^1_2 & q^2_2 & q^3_2\\ \end{bmatrix}_{2 \times 3d_q}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}_{2 \times d_x}W^Q_{d_x \times 3d_q}\\ \begin{bmatrix} k^1_1 & k^2_1 & k^3_1\\ k^1_2 & k^2_2 & k^3_2\\ \end{bmatrix}_{2 \times 3d_k}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}_{2 \times d_x}W^K_{d_x \times 3d_k}\\ \begin{bmatrix} v^1_1 & v^2_1 & v^3_1\\ v^1_2 & v^2_2 & v^3_2\\ \end{bmatrix}_{2 \times 3d_v}=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}_{2 \times d_x}W^V_{d_x \times 3d_v}\)

• 计算query、key间的相似度得分
  \(score(Q,K)=\begin{bmatrix} s^1_{11} & s^1_{12}\\ s^1_{21} & s^1_{22}\\s^2_{11} & s^2_{12}\\s^2_{21} & s^2_{22}\\s^3_{11} & s^3_{12}\\s^3_{21} & s^3_{22} \end{bmatrix}_{3\cdot 2 \times 2}=\frac{1}{\sqrt{d_q}}\begin{bmatrix} q^1_1 & q^1_1 \\ q^1_2 & q^1_2 \\ q^2_1 & q^2_1\\ q^2_2 & q^2_2 \\ q^3_1 & q^3_1 \\ q^3_2 & q^3_2\end{bmatrix}_{3\cdot 2 \times 2}\begin{bmatrix} k^1_1 & k^1_2 \\ k^1_1 & k^1_2 \\ k^2_1 & k^2_2\\ k^2_1 & k^2_2 \\ k^3_1 & k^3_2 \\ k^3_1 & k^3_2\end{bmatrix}_{3\cdot 2 \times 2}\)

• 对相似度得分矩阵求softmax

• 乘以value向量得到各自注意力模块输出，并乘以输出权重矩阵得到最终输出矩阵O，其最终还是得到了多头注意力的输出，其为输出词向量维度，如果其维度等于输入词向量维度时，输出和输入的尺度是一致的，因此多头注意力机制本质仍是特征抽取器。
  \(\\ Z=\begin{bmatrix} z^1_1 \\ z^1_2\\z^2_1 \\ z^2_2\\z^3_1 \\ z^3_2 \end{bmatrix}= \begin{bmatrix} p^1_{11} & p^1_{12}\\ p^1_{21} & p^1_{22} \\ p^2_{11} & p^2_{12}\\ p^2_{21} & p^2_{22} \\ p^3_{11} & p^3_{12}\\ p^3_{21} & p^3_{22} \end{bmatrix}\begin{bmatrix} v_1 \\ v_2 \\ v_1 \\ v_2 \\ v_1 \\ v_2 \end{bmatrix}\\ O_{2\times d_o}=\begin{bmatrix} z^1_1 & z^2_1 & z^3_1 \\ z^1_2 & z^2_2 & z^3_2 \end{bmatrix}_{2\times 3d_z}W^o_{3d_z \times d_o}\)

视频连接

参考连接