TensorFlow05-3 神经网络损失函数(误差计算)

▪ MSE
▪ Cross Entropy Loss(针对分类问题)
▪ Hinge Loss

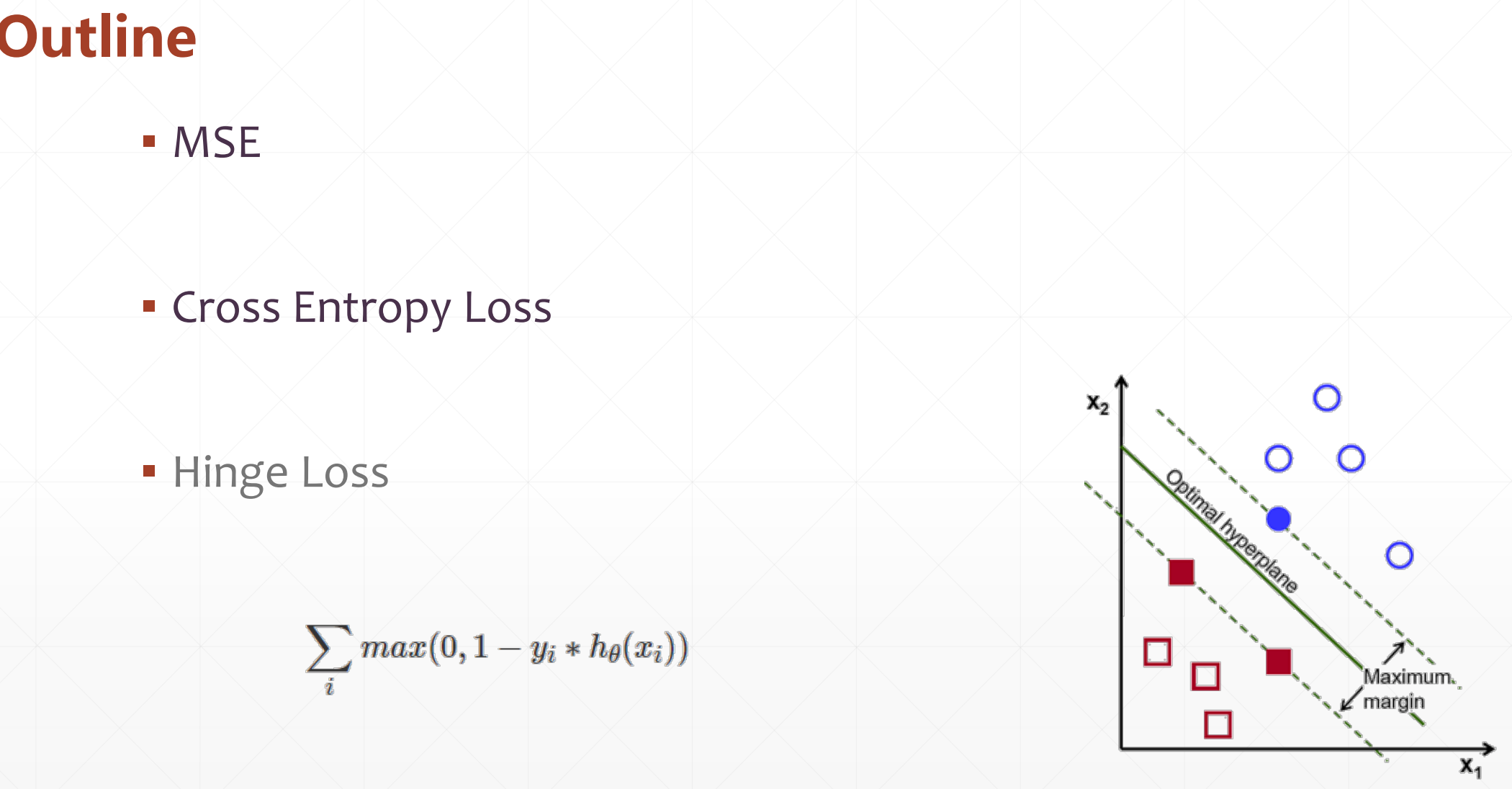
1 MSE

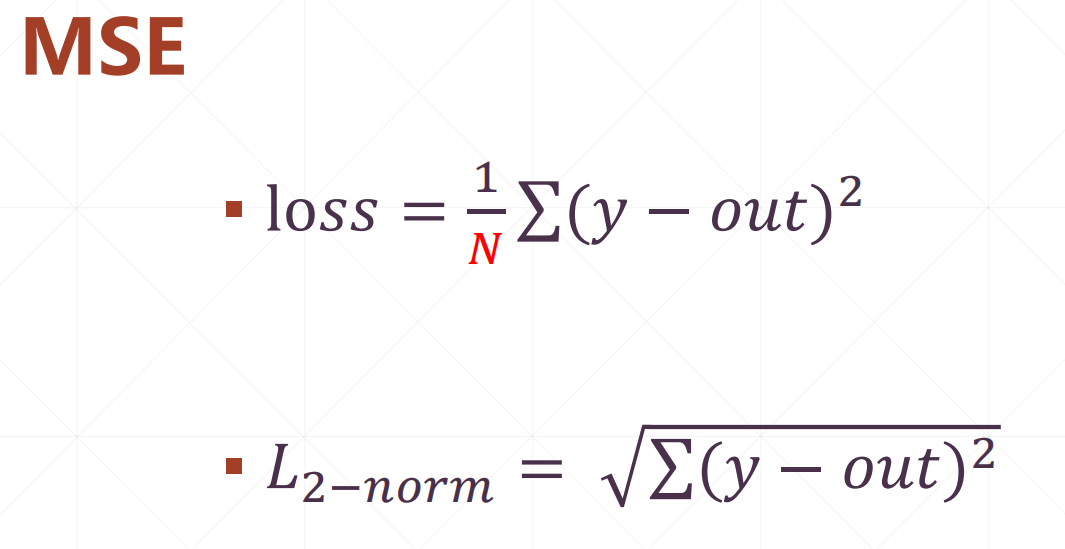
一般这个N都会取一个banch。或者取到一个banch*类别个数b

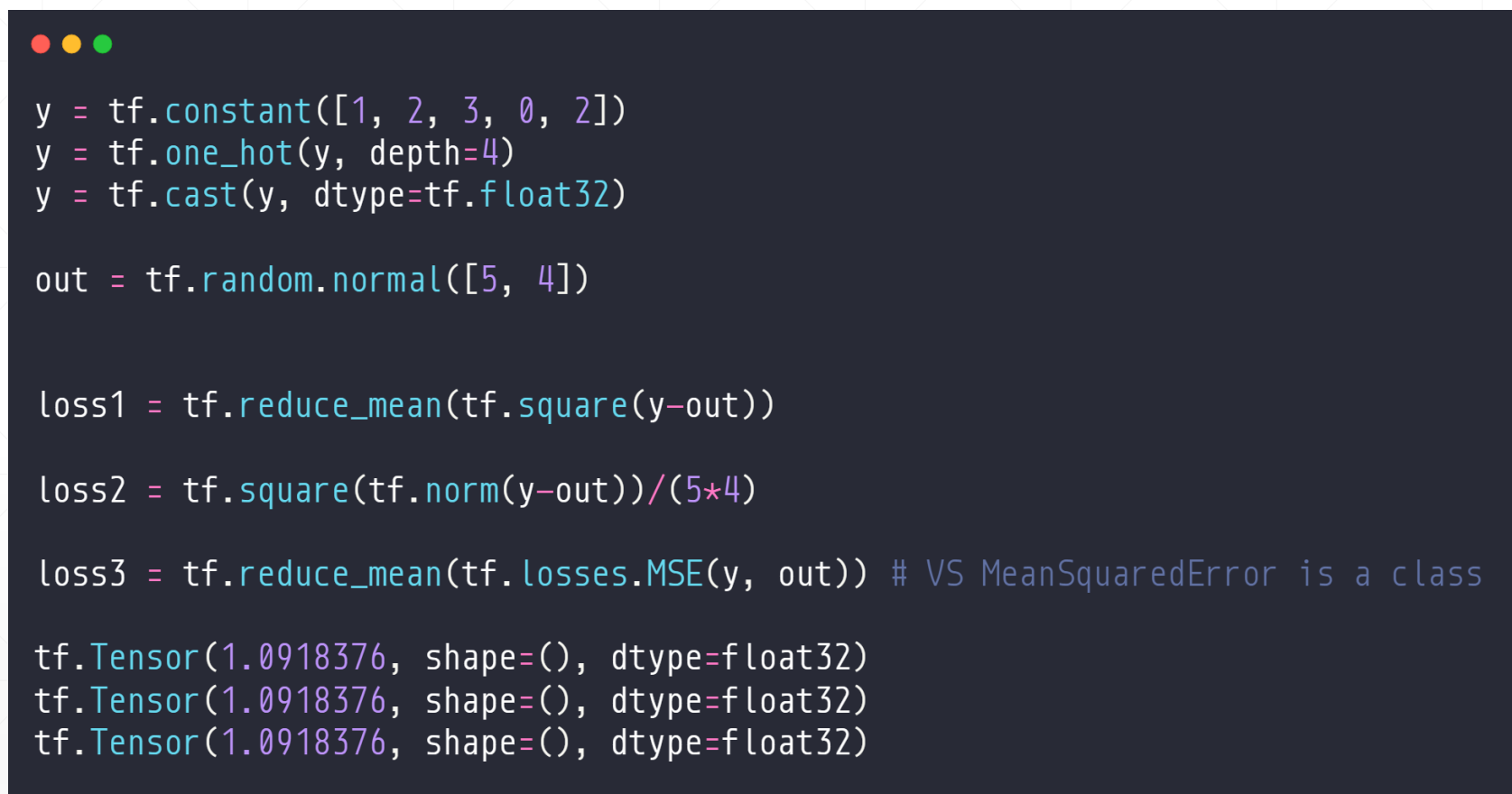
这里有三种求MSE的方法：

loss1=tf.reduce_mean(tf.squaare(y-out))
loss2=tf.squre(tf.norm(y-out))/(banch*类别个数b)
loss3=tf.reduce_mean(tf.losses.MSE(y,out))

2 Entropy（熵）

这是一个专门针对二分类求误差的

就是一个东西熵越小，信息量越大，也就是惊喜度最大

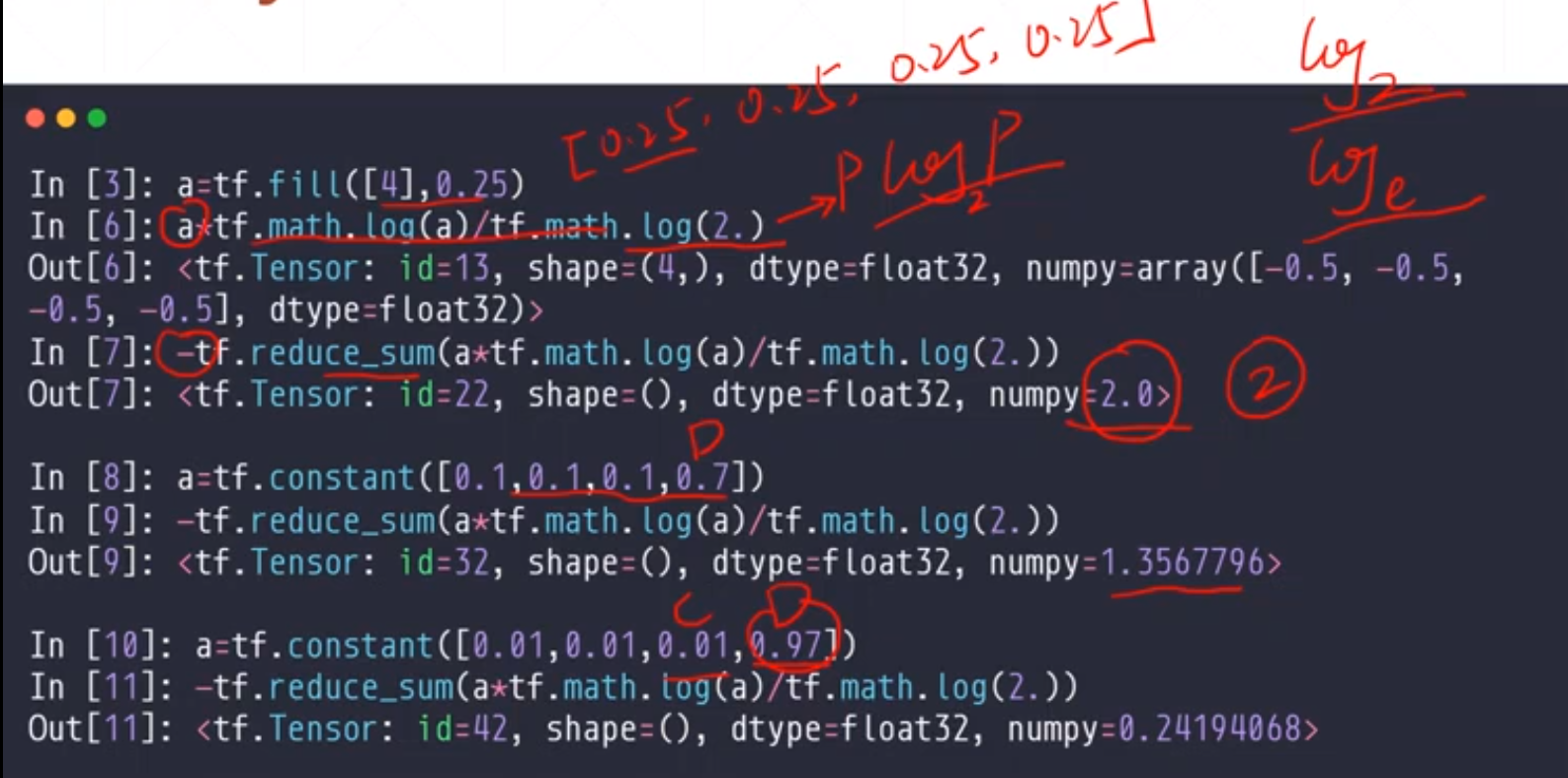
对于上面的例子[0.25,0.25,0.25,0.25]这四个求的值是很大的，因为没有什么惊喜度。
对于[0.01,0.01,0.01,0.97]这个惊喜度是最高的

3 Cross Entropy(交叉熵)

在这里H(p,q)=H(p)+DKL(p|q)
如果p==q的时候DKL=0，此时Minima:H(p|q)=H(p)
如果这个p是one-hot encoding的时候的话：
h(p:[0,1,0])=-log1=0
H([0,1,1],[p0,p1,p2])=0+DKL(p|q)=-l*log(qi)
q:prob(预测值)，p:(真实值)，loss=H(p,q),如果DKL(p|q)=0的此时loss最小，及此时p=q,此时误差最小

4 Binary Classification(二分类)

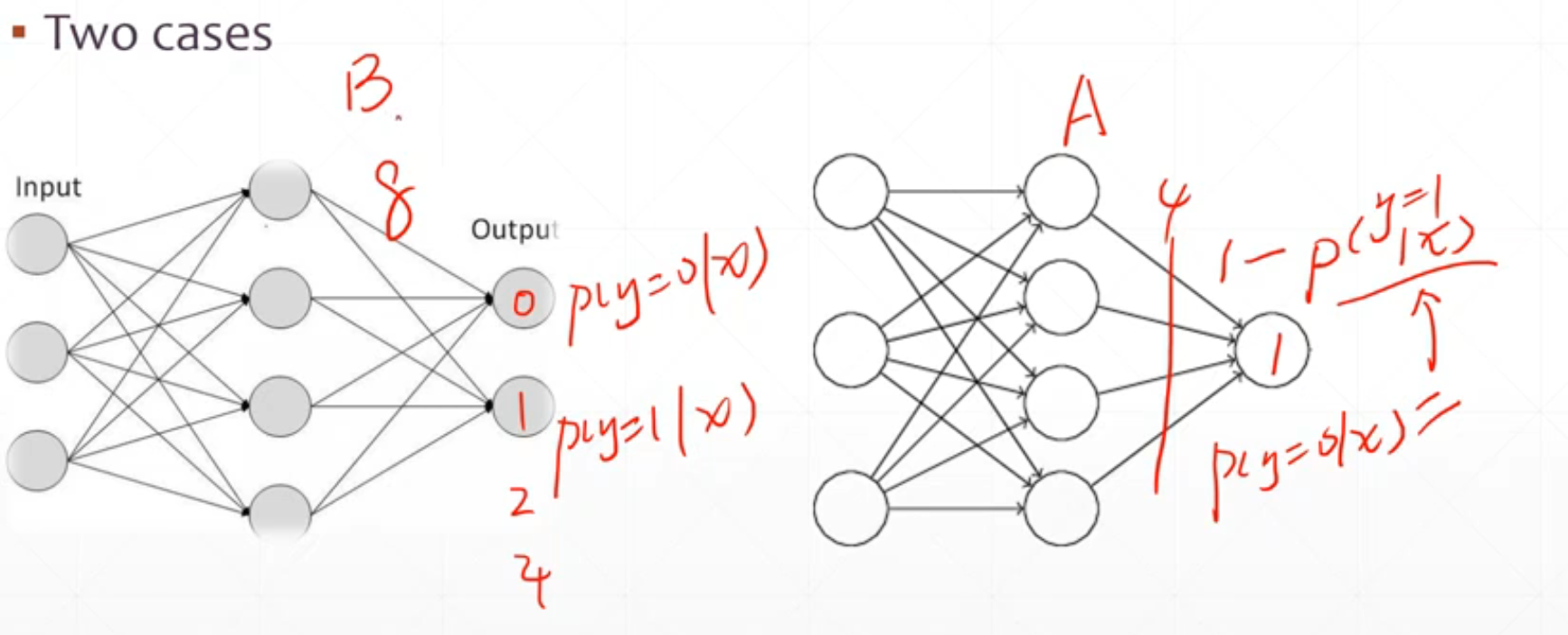
现在这两种都可以
single output:
当p:one-hot的时候，我们的loss=H(p,q)=0+DKL
这里的DKL=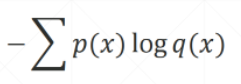由于我们的这个是只有一个是1，剩下的全是0，所以这个loss=-1*log(qi),此时p=q的时候loss最小

4.1 Single output（单号输出节点）

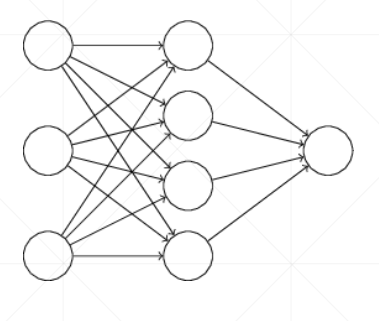
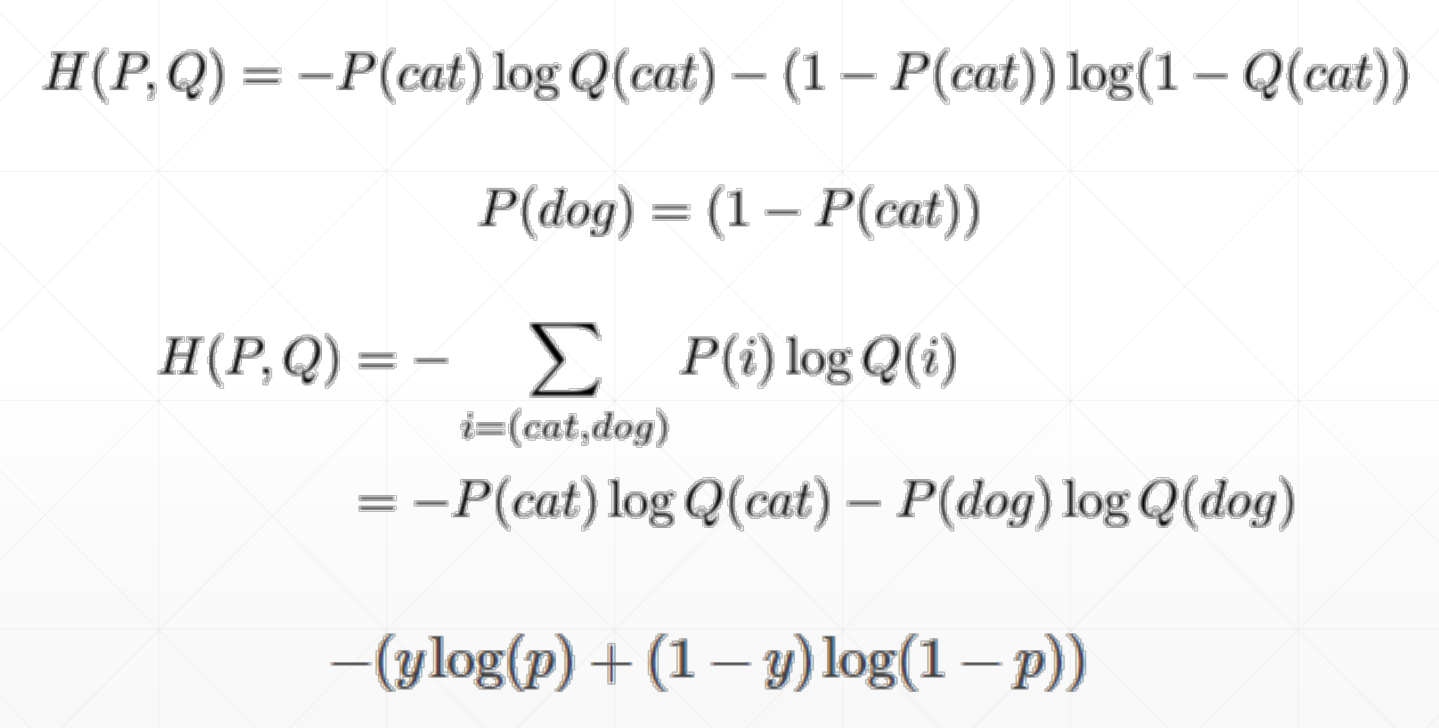
4.2 Classification（多分类）

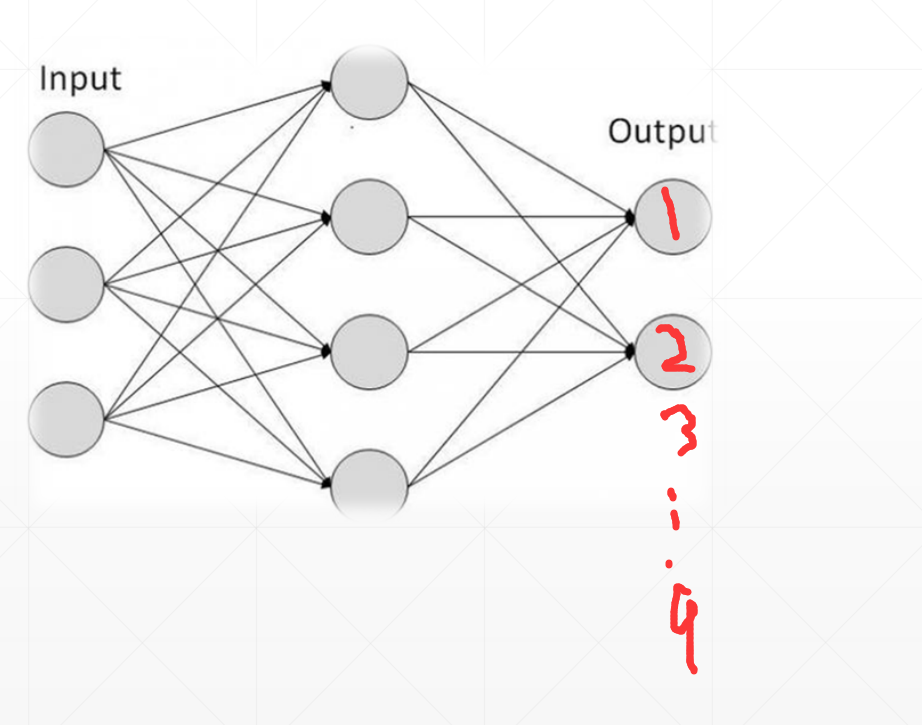
这里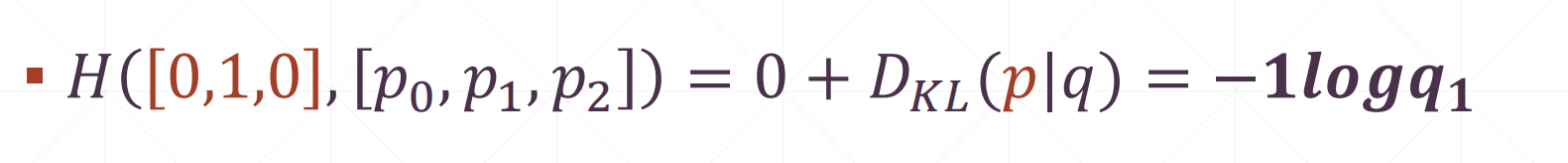

例如这两个例子：

Q1=[0.4,0.3,0.05,0.05,0.2]这个求的值为0.916，但是Q1=[0.98,0.01,0,0,0.01]的时候我们的H(p1,p2,p3,p4)=0.02,这个数值越接近于0越好。
我们在计算多分类问题的时候很简单：API

tf.losses.categorical_crossentropy([],[])
在这里前面的一个是真实值，后面的一个是预测值

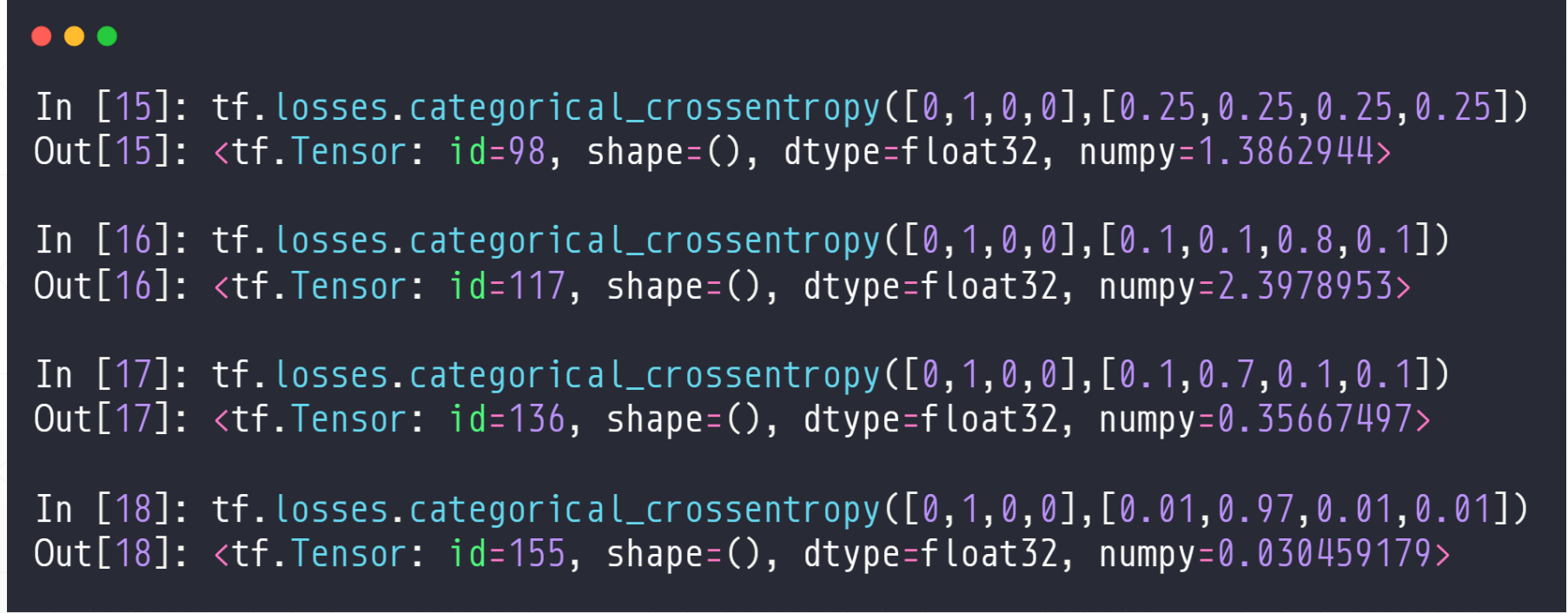
我们看最后一个我们预测对了，且非常肯定的话，我们的这个值非常小。

Why not MSE?

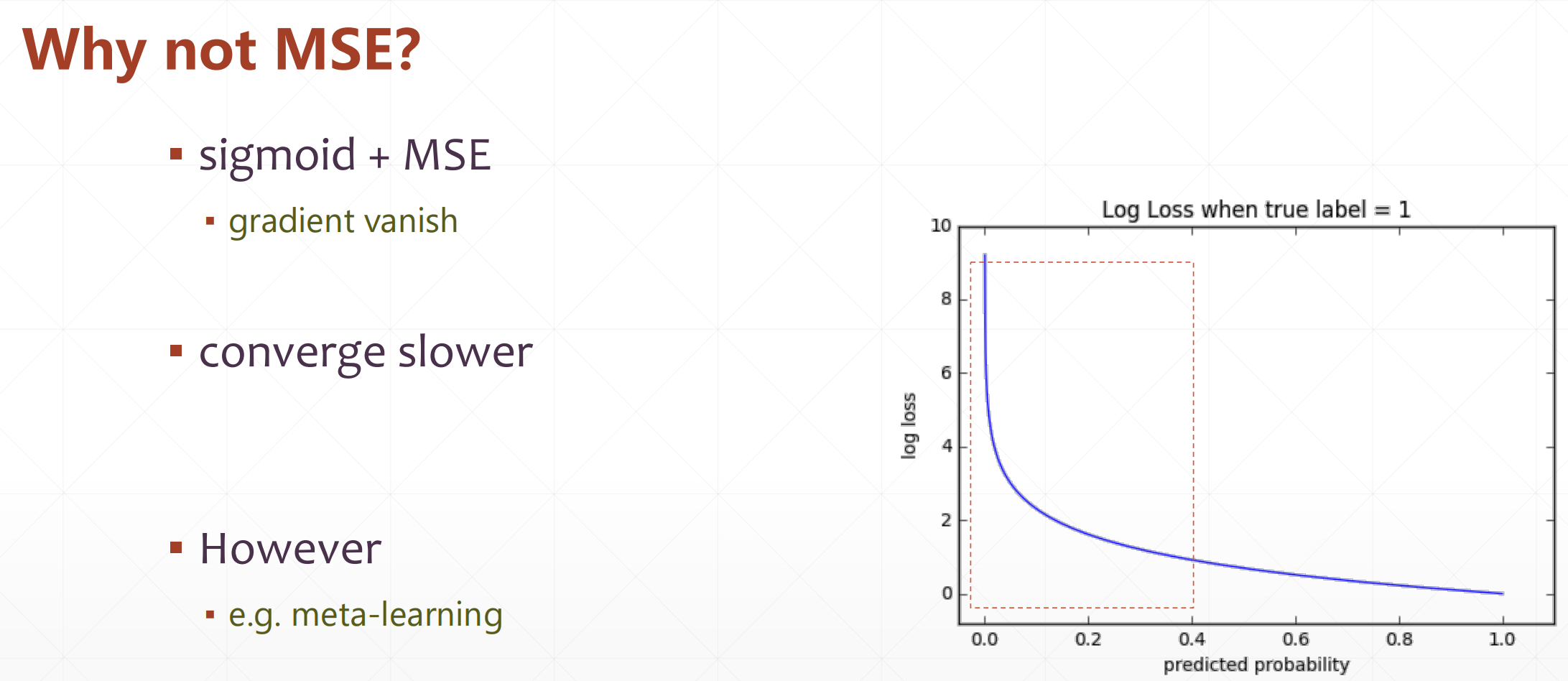
这个sigmoid在一开始和后面的时候会出现梯度消失的情况。
我们看一个二分类问题，我们对于这个out,我们首先做softmax在做cross-entropy。但是这样会有一个数值不稳定的情况，所以我们在做的时候我们通常情况下把后面两个合并在一起。

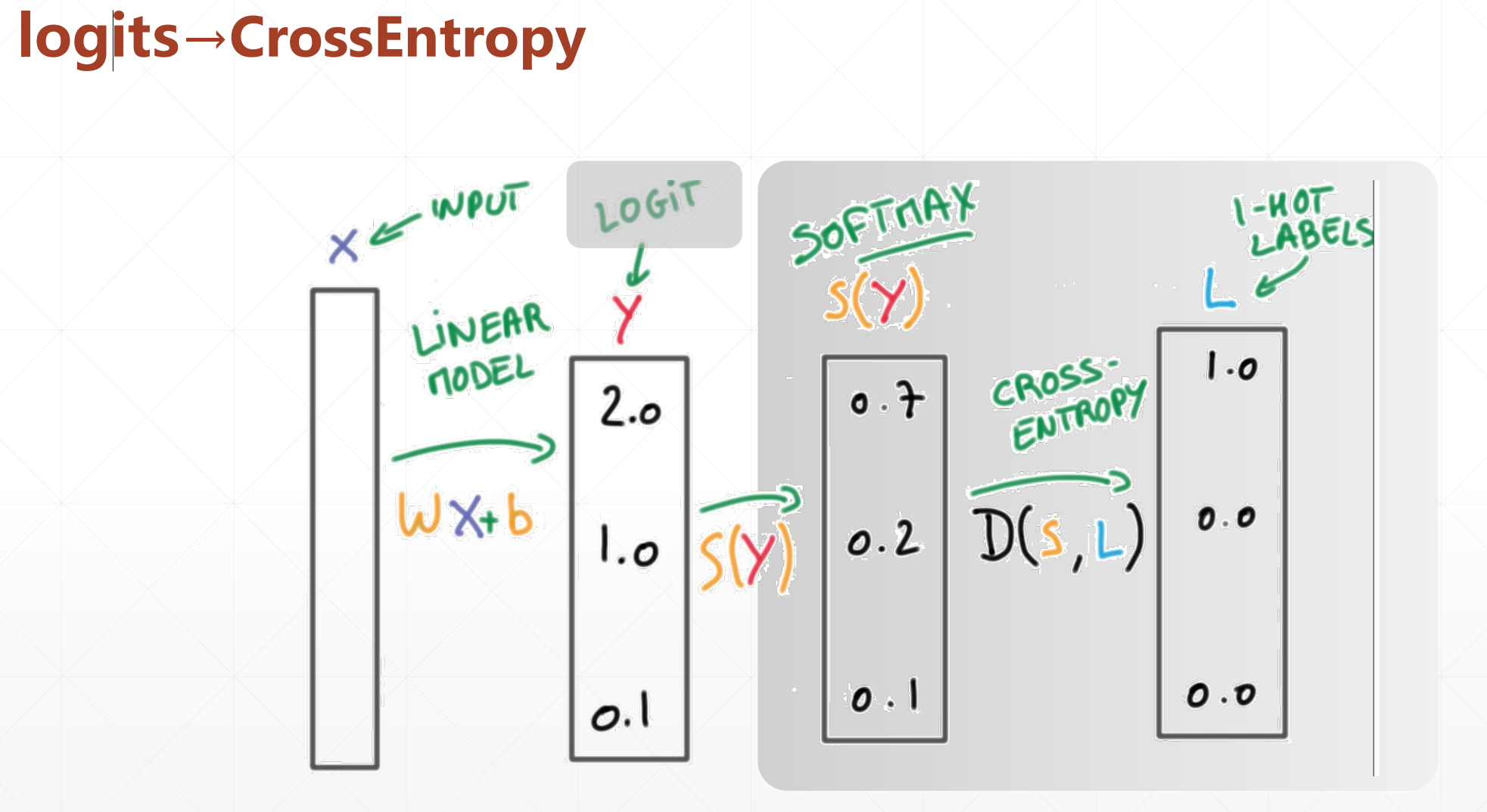
所以我们调用的时候就调用这个：

tf.losses.categorical_crossentropy([],logits,from_logits=True)
[]这个里面必须是one-hot,logits就是out.

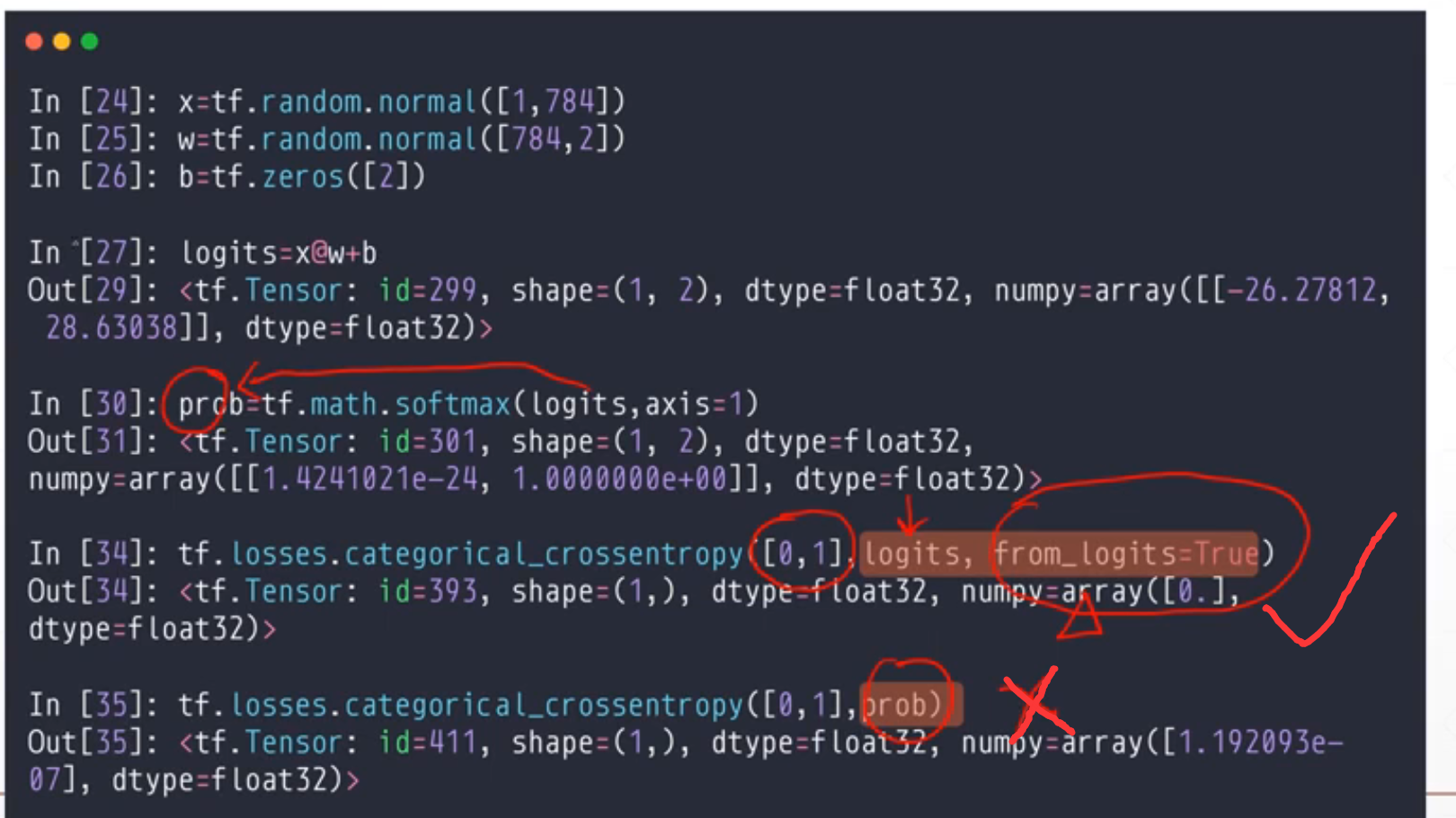
所以我们只需要进行上面一个函数就行，tf.losses.categorical_crossentropy([],out,from_logits=True)
然后我们就不需要softmax了，之间用上面的一个就行，防止数值不稳定