用三种不同颜色为网格涂色（状态压缩dp）

1931. 用三种不同颜色为网格涂色

给你两个整数 m 和 n 。构造一个 m x n 的网格，其中每个单元格最开始是白色。请你用 红、绿、蓝 三种颜色为每个单元格涂色。所有单元格都需要被涂色。

涂色方案需要满足：不存在相邻两个单元格颜色相同的情况 。返回网格涂色的方法数。因为答案可能非常大， 返回 对 109 + 7 取余 的结果。

 

示例 1：

输入：m = 1, n = 1
输出：3
解释：如上图所示，存在三种可能的涂色方案。
示例 2：

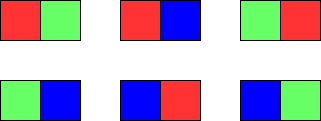
输入：m = 1, n = 2
输出：6
解释：如上图所示，存在六种可能的涂色方案。
示例 3：

 

输入：m = 5, n = 5
输出：580986
 

提示：

1 <= m <= 5
1 <= n <= 1000

这个题是一个状态压缩dp,dp[i][s]指的是第i行状态为s的方案数

设状态 f(i,S) 表示处理了前 i 列，且第 i 列的状态为 S 时的方案数。其中 S 为三进制的掩码。
初始时，f(0,S)=1，其余为 0 待定。
转移时，对于一个合法的 f(i−1,S1)，枚举合法的 S2，且保证 S1 和 S2 合法，转移 f(i,S2)=f(i,S2)+f(i−1,S1).
最终答案为 ∑Sf(n−1,S)。
通过预处理，可以得到所有合法的 S 以及合法的转移。

class Solution {
public:
    int f[1005][10005];
    int mod=1e9+7,M;
    bool check(int s){//判断状态为s的这一行合不合法
        int last=-1;
        for(int i=0;i<M;i++){
            if(s%3==last){
                return false;
            }
            last=s%3;
            s/=3;
        }
        return true;
    }
    bool check_n(int x,int y){//判断状态为x和y是不是合法
        for(int i=0;i<M;i++){
            if(x%3==y%3){
                return false;
            }
            x/=3;
            y/=3;
        }
        return true;
    }
    int colorTheGrid(int m, int n) {
        M=m;
        int tot=1;
        for(int i=1;i<=m;i++){
            tot*=3;
        }
        for(int i=0;i<tot;i++){
            if(check(i)) f[1][i]=1;
        }
        for(int i=2;i<=n;i++){
            for(int j=0;j<tot;j++){
                if(check(j)){
                    for(int k=0;k<tot;k++){
                        if(!check_n(j,k)) continue;
                        f[i][j]=(f[i][j]+f[i-1][k])%mod;
                    }
                }
            }
        }
        int ans=0;
        for(int i=0;i<tot;i++){
            ans=(ans+f[n][i])%mod;
        }
        return ans;
    }
};