图论拆点（二维最短路）

例一：

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

 

示例 1：

 

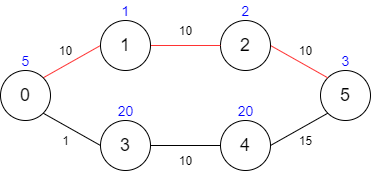
输入：maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：11
解释：最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。
示例 2：

 

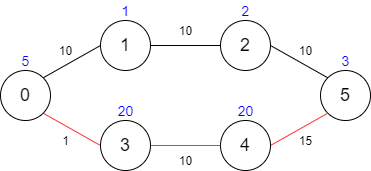
输入：maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：48
解释：最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。
示例 3：

输入：maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：-1
解释：无法在 25 分钟以内从城市 0 到达城市 5 。
 

提示：

1 <= maxTime <= 1000
n == passingFees.length
2 <= n <= 1000
n - 1 <= edges.length <= 1000
0 <= xi, yi <= n - 1
1 <= timei <= 1000
1 <= passingFees[j] <= 1000 
图中两个节点之间可能有多条路径。
图中不含有自环。

 

上面的是官方的题解，其实这个要用到拆点的技巧，f[t][i]指的是使用恰好t分钟到达i需要的最少通行费总和。

其实就是加上了一维，时间的维度

 

#define x first
#define y second
typedef pair<int,int> PII;
const int N=1010,M=2010,INF=0x3f3f3f3f;
int h[N],e[M],w[M],ne[M],cnt;
int dis[N][N];
bool vis[N][N];
class Solution {
public:
    void add(int a,int b,int c){
        e[cnt]=b;
        w[cnt]=c;
        ne[cnt]=h[a];
        h[a]=cnt++;
    }
    int minCost(int m, vector<vector<int>>& edges, vector<int>& pf) {
        int n=pf.size();
        memset(h,-1,sizeof(h)),cnt=0;
        for(auto e: edges){
            int a=e[0],b=e[1],c=e[2];
            add(a,b,c);
            add(b,a,c);
        }
        memset(dis,0x3f,sizeof(dis));
        dis[0][0]=pf[0];
        queue<PII> q;
        q.push({0,0});
        while(!q.empty()){
            auto t=q.front();
            q.pop();
            vis[t.x][t.y]=false;
            for(int i=h[t.x];~i;i=ne[i]){
                int x=e[i],y=t.y+w[i];
                if(y>m){
                    continue;
                }
                if(dis[x][y]>dis[t.x][t.y]+pf[x]){
                    dis[x][y]=dis[t.x][t.y]+pf[x];
                    if(!vis[x][y]){
                        vis[x][y]=true;
                        q.push({x,y});
                    }
                }
            }
        }
        int res=INF;
        for(int i=0;i<=m;i++){
            res=min(res,dis[n-1][i]);
        }
        if(res==INF){
            res=-1;
        }
        return res;
    }
};

例二：

小明和小芳出去乡村玩，小明负责开车，小芳来导航。

小芳将可能的道路分为大道和小道。

大道比较好走，每走 1 公里小明会增加 1 的疲劳度。

小道不好走，如果连续走小道，小明的疲劳值会快速增加，连续走 s 公里小明会增加 s2的疲劳度。

例如：有 5 个路口，1 号路口到 2 号路口为小道，2 号路口到 3 号路口为小道，3 号路口到 4 号路口为大道，4 号路口到 5 号路口为小道，相邻路口之间的距离都是 2 公里。

如果小明从 1 号路口到 5 号路口，则总疲劳值为 (2+2)^2+2+2^2=16+2+4=22。

现在小芳拿到了地图，请帮助她规划一个开车的路线，使得按这个路线开车小明的疲劳度最小。

输入格式

输入的第一行包含两个整数 n,m，分别表示路口的数量和道路的数量。路口由 1 至 n 编号，小明需要开车从 1 号路口到 n 号路口。

接下来 m 行描述道路，每行包含四个整数 t,a,b,c，表示一条类型为 t，连接 a 与 b 两个路口，长度为 c公里的双向道路。其中 t 为 0 表示大道，t 为 1 表示小道。

保证 1 号路口和 n 号路口是连通的。

输出格式

输出一个整数，表示最优路线下小明的疲劳度。

数据范围

对于 30% 的评测用例，1≤n≤8，1≤m≤10；
对于另外 20% 的评测用例，不存在小道；
对于另外 20% 的评测用例，所有的小道不相交；
对于所有评测用例，1≤n≤500，1≤m≤10^5，1≤a,b≤n，t 是 0 或 1，c≤10^5。
保证答案不超过 10^6。

输入样例：

6 7
1 1 2 3
1 2 3 2
0 1 3 30
0 3 4 20
0 4 5 30
1 3 5 6
1 5 6 1

输出样例：

76

样例解释

从 1 走小道到 2，再走小道到 3，疲劳度为 5^2=25；然后从 3 走大道经过 4 到达 5，疲劳度为 20+30=50；最后从 5 走小道到 6，疲劳度为 1。

总共为 76。

 

 

Dis[i][j]表示从1到点i的最短距离，第二维j表示1到i点这条路径上最后那段(连接i)的小路的长度。如果1到i的路径最后那段是大路，那么j 置为0.

那最后的答案是什么呢？ 是dis[n][i]，枚举每个i从0到1000，取出最小值即可。

 

 

这个题会卡掉spfa的，然后要用堆优化的dijkstra()

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
#define x first
#define y second
using namespace std;
const int INF=0x3f3f3f3f;
const int N=3e3+100;
const int M=3e3+100;
const int maxn=2e5+100;
int dis[N][M];
bool st[N][M];
struct node{
    int e,ne,w,f;//最短 
}edge[maxn];
int head[maxn]; 
int cnt=0;
struct Node{
    int x,y,v;
    bool operator<(const Node& t)const{
        return v>t.v;
    }
}; 
void add(int a,int b,int c,int w){
    edge[cnt].e=b;
    edge[cnt].ne=head[a];
    edge[cnt].f=c;
    edge[cnt].w=w;//最短 
    head[a]=cnt++;
}
void dijkstra(){
    priority_queue<Node>q;
    memset(dis,0x3f,sizeof(dis));
    q.push({1,0,0});
    dis[1][0]=0;
    while(!q.empty()){
        Node t=q.top();
        q.pop();
        if(st[t.x][t.y]) continue;
        st[t.x][t.y]=1;
        for(int i=head[t.x];~i;i=edge[i].ne){
            int x=edge[i].e,y=t.y;
            if(edge[i].f){
                y+=edge[i].w;
                if(y<=1000){
                    if(dis[x][y]>t.v- t.y * t.y + y * y){
                        dis[x][y]=t.v- t.y * t.y + y * y;
                        if(dis[x][y]<=INF){
                            q.push({x,y,dis[x][y]});
                        }
                    }
                }
            }
            else{
                if(dis[x][0]>t.v+edge[i].w){
                    dis[x][0]=t.v+edge[i].w;
                    if(dis[x][0] <= INF)
                        q.push({x,0, dis[x][0]});
                }
            }    
        }
    }
}
int main(){
    int n,m;
    memset(head,-1,sizeof(head));
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int a,b,c,w;
        cin>>c>>a>>b>>w;
        add(a,b,c,w);
        add(b,a,c,w);
    } 
    dijkstra();
    int ans=INF;
    for(int i=0;i<=1000;i++){
        ans=min(ans,dis[n][i]);
    }
    cout<<ans<<endl;
}