算法——最小生成树的关键边和伪关键边
给你一个 n 个点的带权无向连通图,节点编号为 0 到 n-1 ,同时还有一个数组 edges ,其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集,它连接了所有节点且没有环,而且这些边的权值和最小。
请你找到给定图中最小生成树的所有关键边和伪关键边。如果从图中删去某条边,会导致最小生成树的权值和增加,那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。
请注意,你可以分别以任意顺序返回关键边的下标和伪关键边的下标。
添加链接描述
解题思路:
- 这道题是一个求最小生成树的问题,底层还是用Kruskal算法求最小最生成树的权重;
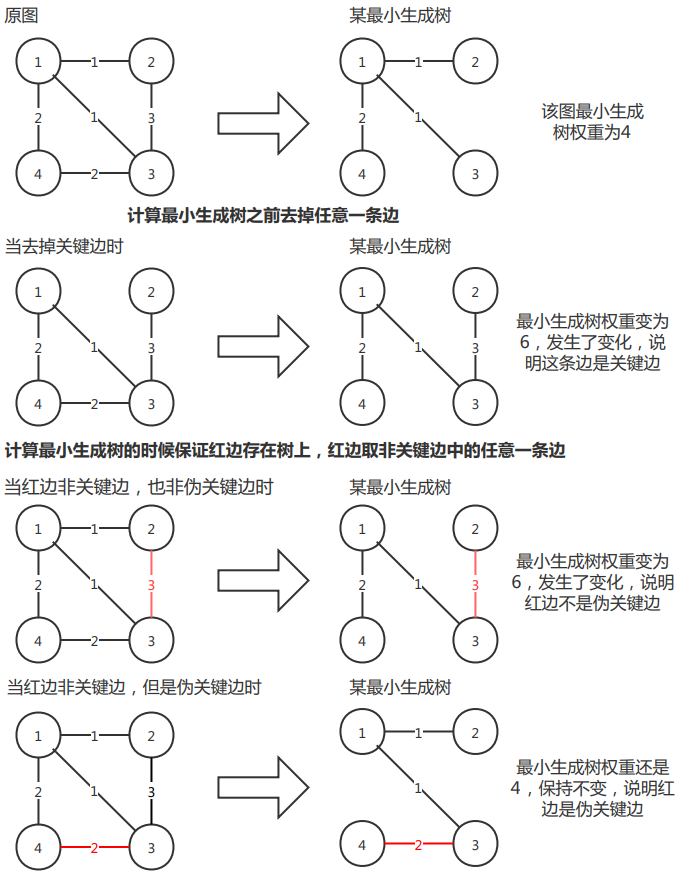
- 所谓关键边,就是原图中去掉了这条边,图的最小生成树权重值就会变化;
- 所谓伪关键边,就是排除关键边,树中提前加上这条边,图的最小生成树权重值不会发生变化;
- 根据上面这个思路,就很好做了,第一步,只需要先求出所有边存在情况下的最小生成树权重;
- 第二步,求分别去掉每一条边时,最小生成树的权重是否会发生变化,如果发生变化了,那它肯定是关键边;
- 第三步,非关键边中,求树上分别提前加上每一条边时,最小生成树的权重是否会发生变化,如果没有发生变化了,那它肯定是伪关键边。
为什么在判断伪关键边的时候,需要排除关键边呢?
因为我们是通过求树上分别提前加上每一条边时,最小生成树的权重是否会发生变化的依据,来判断伪关键边的,而关键边当然也包含了这个性质,但是伪关键边不包含第二步的性质,所以,先判断得出关键边,然后再第三步判断时剔除关键边。
图中去掉关键边和树中添加非关键边对最小生成树权重的影响,如下图所示。
// 定义边
class Edge {
// 分别表示当前边的序号、起点、终点、权重
public int id, a, b, weight;
public Edge(int i, int _a, int _b, int w) {
id = i;
a = _a;
b = _b;
weight = w;
}
}
class Solution {
public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
// 并查集集合初始化
List<Integer> p = new ArrayList<>();
for(int i = 0; i < n; i++) {
p.add(i);
}
// 将所有边添加到列表当中
List<Edge> nes = new ArrayList<>();
for(int i = 0; i < edges.length; i++) {
nes.add(new Edge(i, edges[i][0], edges[i][1], edges[i][2]));
}
// 第一步,计算最小生成树的权重
int minTreeWeight = minTreeWeightCal(new ArrayList<>(p), nes, 0);
// 初始化答案列表
List<List<Integer>> res = new ArrayList<>();
res.add(new ArrayList<>());
res.add(new ArrayList<>());
// 复制一个临时边集,用于删边操作
List<Edge> tempEdges = new ArrayList<>(nes);
// 第二步,先枚举所有边,查看这条边是不是关键边
for(Edge e : nes) {
// 如果从边集中删除了这条边,最小生成树的权重发生了变化,说明这是关键边
tempEdges.remove(e);
if(minTreeWeight != minTreeWeightCal(new ArrayList<>(p), tempEdges, 0)) {
res.get(0).add(e.id);
}
// 将删去边放回去
tempEdges.add(e);
}
// 第三步,再判断每条边是不是伪关键边
for(Edge e : nes) {
// 如果当前边是关键边,那就肯定不是伪关键边
if(res.get(0).contains(e.id)) continue;
List<Integer> tp = new ArrayList(p);
// 提前连上这条边的两个端点
tp.set(e.a, e.b);
// 判断权重是否和之前相同
if(minTreeWeight == minTreeWeightCal(tp, tempEdges, e.weight)) {
// 连上了这条边,最小生成树的权重还是一样的,说明这是伪关键边
res.get(1).add(e.id);
}
}
return res;
}
// Kruskal算法求最小生成树,参数分别表示点的并查集,边列表,初始权重
private int minTreeWeightCal(List<Integer> p, List<Edge> nes, int w) {
// 对边从小到大进行排序
Collections.sort(nes, (a, b) -> a.weight - b.weight);
for(Edge e : nes) {
int a = find(p, e.a), b = find(p, e.b);
if(a != b) {
w += e.weight;
p.set(a, b);
}
}
return w;
}
// 并查集模板方法,求当前元素所在集合的根元素
private int find(List<Integer> p, int x) {
if(p.get(x) != x) {
p.set(x, find(p, p.get(x)));
}
return p.get(x);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号