前缀和的总结
还是从潜入深做做题
洛谷P8218求区间和
对于前缀和题目,数组下标一般从1开始取,这样在计算s[i]=s[i-1]+a[i]时s[i-1]最小就是s[0],直接定义s[0]=0;
处理出前缀和数组我们求区间和时可以用两个前缀和做差s[r]-s[l-1]即为从l到r的区间和
这里简单理解为什么是l-1,计算的时候不能把a[l]也减了吧。
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N],s[N];
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
s[i]=s[i-1]+a[i];
}
int m;
cin>>m;
while(m--)
{
int l,r;
cin>>l>>r;
cout<<s[r]-s[l-1]<<endl;
}
return 0;
}
洛谷P2280激光炸弹
上一道题是一维前缀和,这个题是二维的。二维前缀和想象起来比较困难。

这里借用一下董晓老师的图,二维情况下如何处理前缀和呢。
我要求s[i][j]的大小从图中可以看出我可以通过s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]来得到
那么如何处理区间和呢?给定(x1,y1)、(x2,y2)
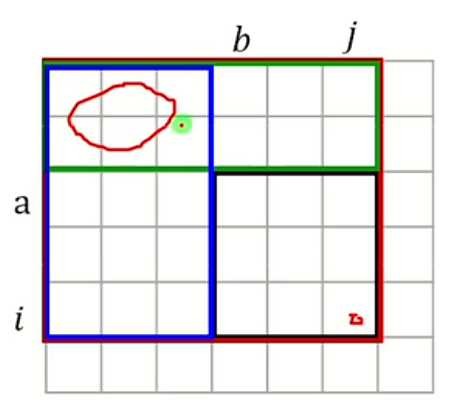
我们运用拼凑的方法,用s[x2][y2]减去两块矩形的大小,然后再加上重叠区域就是区间和。
公式为s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]
#include <bits/stdc++.h>
using namespace std;
const int N=5e3+5;
int s[N][N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
{
int x,y,v;
cin>>x>>y>>v;
s[++x][++y]+=v;
}
for(int i=1;i<=N-4;i++)
{
for(int j=1;j<=N-4;j++)
{
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
}
}
int ans=0;
for(int i=m;i<=N-4;i++)
{
for(int j=m;j<=N-4;j++)
{
int num=s[i][j]-s[i][j-m]-s[i-m][j]+s[i-m][j-m];
ans=max(ans,num);
}
}
cout<<ans;
return 0;
}
这里再附加一个AcWing的激光炸弹
和洛谷不一样的是这里的轰炸范围是可以远大于地图范围的,所以我特判了一下
#include <bits/stdc++.h>
using namespace std;
const int N=5e3+5;
int s[N][N];
int main()
{
int n,m;
cin>>n>>m;
for(int i=0;i<n;i++)
{
int x,y,v;
cin>>x>>y>>v;
s[++x][++y]+=v;
}
for(int i=1;i<=N-4;i++)
{
for(int j=1;j<=N-4;j++)
{
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
}
}
int ans=0;
if(m>=N)
{
ans=s[N-4][N-4]-s[N-4][1-1]-s[1-1][N-4]+s[1-1][1-1];
cout<<ans;
return 0;
}
for(int i=m;i<=N-4;i++)
{
for(int j=m;j<=N-4;j++)
{
int num=s[i][j]-s[i][j-m]-s[i-m][j]+s[i-m][j-m];
ans=max(ans,num);
}
}
cout<<ans;
return 0;
}
AcWing796 子矩阵的和
这个是二维前缀和模板题
#include <bits/stdc++.h>
using namespace std;
const int N=5e3+5;
int s[N][N],a[N][N];
int main()
{
int n,m,q;
cin>>n>>m>>q;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++){
cin>>a[i][j];
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
}
while(q--)
{
int x1,x2,y1,y2;
cin>>x1>>y1>>x2>>y2;
cout<<s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]<<endl;
}
return 0;
}
AcWing 562. 壁画
这个题里面,一定是先画画然后墙再坏,所以我们所画的墙的数量就是[n/2]上取整。
所以题目就转化为求长度为[n/2]的连续子串的最大和,其实也能想到滑动窗口的方法。
这里先写前缀和的方法吧,滑动窗口等做到会去再做一次。其实看起来感觉就是滑动窗口,从m出发一直向右移动,先计算前m段,然后开始向右移动,抛弃第一段....直到移动到n。计算区间和,取最大值
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=5e6+10;
int a[N];
int main()
{
ios::sync_with_stdio(false);
int t;
cin>>t;
for(int j=1;j<=t;j++)
{
int n;
cin>>n;
string s;
cin>>s;
s=' '+s;
for(int i=1;i<=n;i++)
{
a[i]=s[i]-'0';
a[i]=a[i-1]+a[i];
}
int m=(n+1)/2;
int res=a[m-1];
int mx=0;
for(int i=m;i<=n;i++)
{
mx=max(mx,a[i]-a[i-m]);
}
cout <<"Case #"<<j<<": "<<mx<<endl;
}
return 0;
}
AcWing 4405. 统计子矩阵
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=550;
int a[N][N];
ll s[N][N];
ll sum(int x1,int y1,int x2,int y2)
{
return s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1];
}
int main()
{
int n,m,k;
ios::sync_with_stdio(false);
cin>>n>>m>>k;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
}
}
ll ans=0;
for(int i=1;i<=n;i++)//枚举矩阵的上边
{
for(int j=i;j<=n;j++)//枚举矩阵的下边
{
for(int l=1,r=1;r<=m;r++)
{
while(l<=r&&sum(i,l,j,r)>k) l++;
if(l<=r) ans+=r-l+1;
}
}
}
cout<<ans;
return 0;
}
AcWing 1230. K倍区间
这个题目说的很直白,就是区间和是K的倍数,也就是(s[r]-s[l-1])%k0,所以s[r]%ks[l-1]%k,
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5;
int cnt[N];//表示余数为x的个数
int ans;//答案
int n,k;
int s[N];//前缀和数组
signed main()
{
cin>>n>>k;
for(int i=1;i<=n;i++)
{
int a;
cin>>a;
s[i]=(s[i-1]+a)%k;//这里直接取模省下一次循环
ans+=cnt[s[i]];//这里当我们第一次遇到这样的余数时计算不会有效;
//第二次遇到时可以和之前的余数构成所求区间,第三次遇到时会和前两个构成所求区间。
//所以先更新答案再更新cnt数组
cnt[s[i]]++;
}
//注意结果是需要加上cnt[0]的,因为这样的区间本身就满足要求
cout<<ans+cnt[0];
return 0;
}
AcWing 1236. 递增三元组
暴力一定会TLE的,可以尝试用二分的方法。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+5;
int a[N],b[N],c[N];
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++) cin>>a[i];
for(int i=0;i<n;i++) cin>>b[i];
for(int i=0;i<n;i++) cin>>c[i];
sort(a,a+n);
sort(b,b+n);
sort(c,c+n);
ll ans=0;
for(int i=0;i<n;i++)
{
int l=0,r=n-1;
while(l<r)
{
int mid=l+r+1>>1;
if(a[mid]<b[i]) l=mid;//这里尽量往右找a数组中最后一个小于b[i]的数的下标
else r=mid-1;
}
if(a[l]>=b[i])
{
l=-1;
}
int x=l;//二分之后,x就是a数组中小于b[i]的数的个数(x+1)
//因为下标从0开始所以加一
l=0,r=n-1;
while(l<r)
{
int mid=l+r>>1;
if(c[mid]>b[i]) r=mid;
else l=mid+1;
}
if(c[l]<=b[i]){
r=n;
}
int y=r;//二分之后,x就是c数组中小于b[i]的数的个数
//n-y就是大于b[i]的个数。所以如果找不到就设置成n,计算为0
ans+=(ll)(x+1)*(n-y);
}
cout<<ans;
return 0;
}
也可以用前缀和
前缀和怎么解呢,其实和二分方式差不多,我们还是不处理B数组,我们把A数组,C数组每个数字出现的次数存下来,然后用前缀和计算这段区间内的数字个数就行
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+10;
int a[N],b[N],c[N];
int numa[N],numc[N];
int sa[N],sc[N];//前缀和数组
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
numa[++a[i]]++;
}
sa[0]=numa[0];
for(int i=1;i<N;i++)
{
sa[i]=sa[i-1]+numa[i];
}
for(int i=1;i<=n;i++){cin>>b[i];b[i]++;}
for(int i=1;i<=n;i++){
cin>>c[i];
numc[++c[i]]++;
}
sc[0]=numc[0];
for(int i=1;i<N;i++)
{
sc[i]=sc[i-1]+numc[i];
}
ll ans=0;
for(int i=1;i<=n;i++)
{
int B=b[i];
ans+=(ll)sa[B-1]*(sc[N-1]-sc[B]);
}
cout<<ans;
return 0;
}
AcWing 3956. 截断数组
我们先来想一下不能分组的情况,那就是数组总合对3取余不为0;
#include <bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+5;
int s[N];
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>s[i];
s[i]=s[i-1]+s[i];
//前缀和数组的处理:s[i]=s[i-1]+a[i];这里直接用s[i]存a[i]
}
ll ans=0;
if(s[n]%3) cout<<"0";
else {
ll average=s[n]/3;
ll cnt=0;
for(int i=1;i<n;i++)
{
if(s[i]==2*average) ans+=cnt;
if(s[i]==average) cnt++;
}
cout<<ans;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号